A body of mass m is kept on a rough fixed inclined plane of angle of inclination θ=30∘. It remains stationary. Then magnitude of force acting on the body by the inclined plane is equal to :
mg
mgsinθ
mgcosθ
none of these
The correct Answer is:A
To solve the problem of finding the magnitude of the force acting on a body of mass m on a rough fixed inclined plane at an angle of inclination θ=30∘, we can follow these steps:
1. Identify the Forces Acting on the Body:
- The weight of the body W=mg acts vertically downward.
- This weight can be resolved into two components:
- Perpendicular to the inclined plane: W_{\perpendicular} = mg \cos \theta
- Parallel to the inclined plane: W∥=mgsinθ
2. Determine the Normal Force:
- The normal force N exerted by the inclined plane on the body balances the perpendicular component of the weight:
N=mgcosθ
3. Determine the Frictional Force:
- Since the body is stationary, the frictional force f must balance the parallel component of the weight:
f=mgsinθ
4. Calculate the Magnitudes:
- Substitute θ=30∘:
- cos30∘=√32
- sin30∘=12
- Thus, we can calculate:
N=mgcos30∘=mg⋅√32
f=mgsin30∘=mg⋅12
5. Determine the Resultant Force:
- The resultant force R acting on the body by the inclined plane is the vector sum of the normal force and the frictional force. Since these two forces are perpendicular to each other, we can use the Pythagorean theorem:
R=√N2+f2
- Substituting the values of N and f:
R=
⎷(mg⋅√32)2+(mg⋅12)2
R=√m2g2(34+14)=√m2g2=mg
Final Answer:
The magnitude of the force acting on the body by the inclined plane is mg.
- The weight of the body W=mg acts vertically downward.
- This weight can be resolved into two components:
- Perpendicular to the inclined plane: W_{\perpendicular} = mg \cos \theta
- Parallel to the inclined plane: W∥=mgsinθ
- The normal force N exerted by the inclined plane on the body balances the perpendicular component of the weight:
N=mgcosθ
- Since the body is stationary, the frictional force f must balance the parallel component of the weight:
f=mgsinθ
- Substitute θ=30∘:
- cos30∘=√32
- sin30∘=12
- Thus, we can calculate:
N=mgcos30∘=mg⋅√32
f=mgsin30∘=mg⋅12
- The resultant force R acting on the body by the inclined plane is the vector sum of the normal force and the frictional force. Since these two forces are perpendicular to each other, we can use the Pythagorean theorem:
R=√N2+f2
- Substituting the values of N and f:
R=
⎷(mg⋅√32)2+(mg⋅12)2
R=√m2g2(34+14)=√m2g2=mg
The magnitude of the force acting on the body by the inclined plane is mg.
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMSBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 31
7 Videos
- DAILY PRACTICE PROBLEMSBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 32
8 Videos
- DAILY PRACTICE PROBLEMSBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp29
5 Videos
- CURRENT ELECTRICITYBOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Exercise
53 Videos
- ELASTICITY AND VISCOCITYBOOK - RESONANCE ENGLISHCHAPTER - ELASTICITY AND VISCOCITYEXERCISE - Advanced Level Problems
9 Videos
Similar Questions
A block of mass 10 kg is kept on a fixed rough (μ=0.8) inclined plane of angle of inclination 30∘. The frictional force acting on the block is

View SolutionA block of mass m is at rest on a rough inclined plane of angle of inclination θ. If coefficient of friction between the block and the inclined plane is μ, then the minimum value of force along the plane required to move the block on the plane is
View SolutionA block of mass m is kept on an inclined plane is angle inclination θ(<ϕ), where ϕ= angle of friction. Then :

View SolutionA body is kept on a smooth inclined plane having an inclination of 1 in x. Then,
View SolutionA solid cylinder is rolling down a rough inclined plane of inclination θ. Then
View SolutionA uniform thin hemispherical shell is kept at rest and in equilibrium on an inclined plane of angle of inclination θ=30∘ as shown in figure. If the surface of the inclined plane is sufficiently rough to prevent sliding then the angle α made by the plane of hemisphere with inclined plane is :
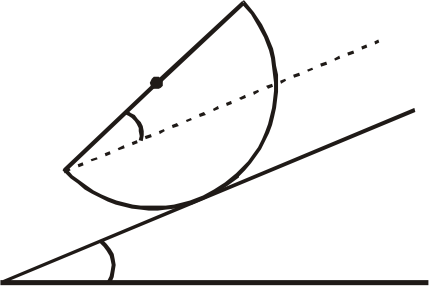
View SolutionA block of mass 5 kg is at rest on a rough inclined surface. If angle of inclination of plane is 60∘, then force applied by it on block is
View SolutionA body of mass 10kg is on a rough inclined plane having an inclination of 30° with the horizontal. If coefficient of friction between the surfaces of contact of the body and the plane is 0.5. Find the least force required to pull the body up the plane.
View SolutionA body of mass 10kg is on a rough inclined plane having an inclination of 30∘ with the horizontal. If co-efficient of friciton between the surface of contact of the body and the plane is 0.25. Find the least force required to pull the body up.
View SolutionA block is kept on a smooth inclined plane of angle of inclination θ that moves wuth a contact acceleration so that the block does not slide relative to the inclined plane. If the inclined plane stops the normal contact force offered by the plane on the block changes by a factor
View Solution
