Calculate the acceleration of block A and B in cases (a),(b), and (c ).



(a) For block 2M,2T=2Ma …(i)
For block M,Mg−t=M2a …(ii)
Solving equation (i) and (ii), we get a=g/3
(b) For block 2M,
2Mgsinθ−T'=2Ma...(i)
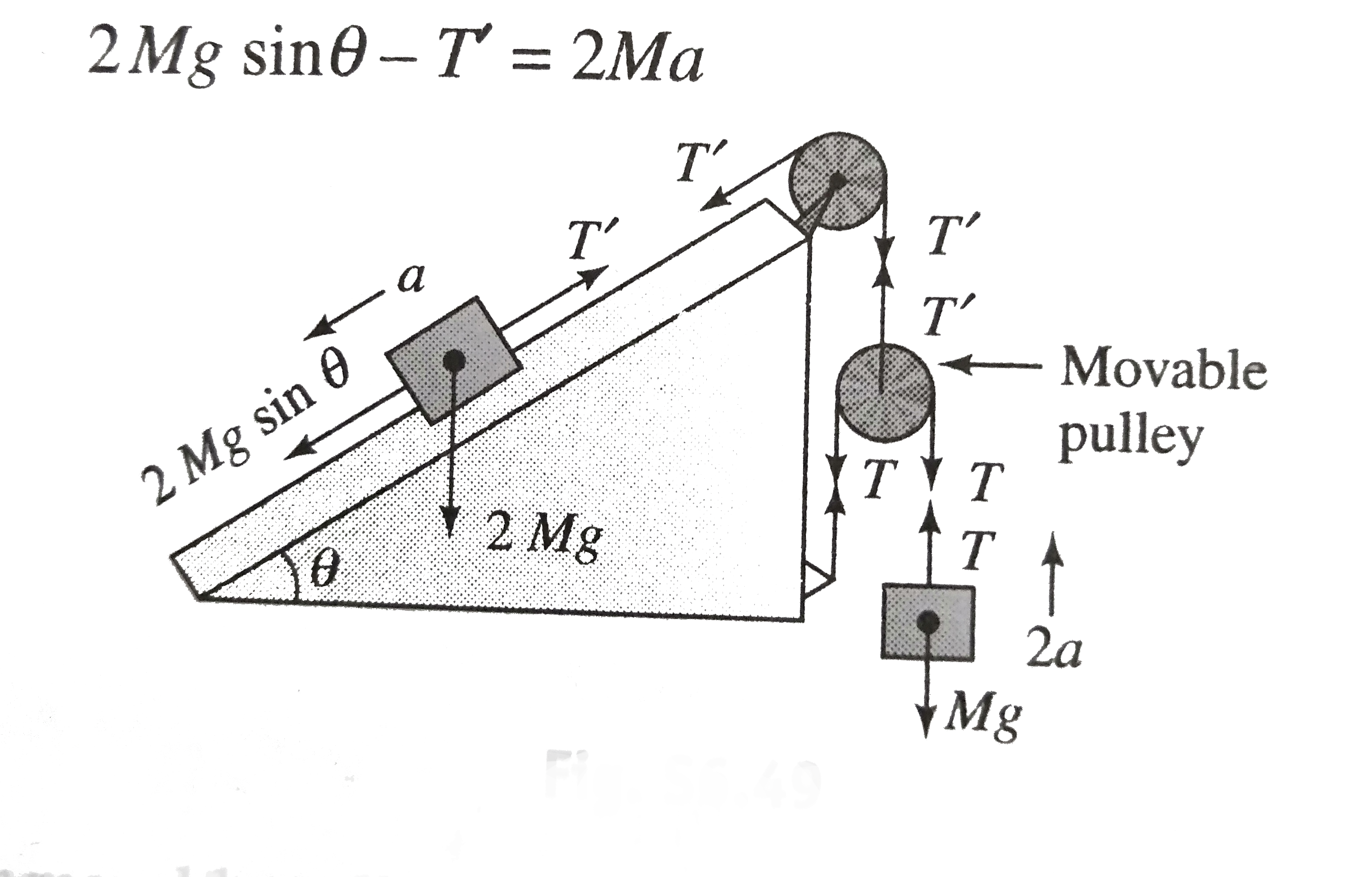
For movable pulley,
T'−2T=0×a⇒T'=2T ...(ii)
For block M,T−Mg=M2a ...(iii)
Solving eq, (i), (ii) , and (iii), we get a=g[sinθ−1]3
This is negative, hence direction of accelerations will be opposite to those shown in fig.
Note: Here we assume that the itblock 2M is moving down the plane. You may assume that it is moving up the plane. The magnitude of the acceleration found will remain the same.
(c) For block 2M,
2Mgsinθ−T=2M(2a) ...(i)
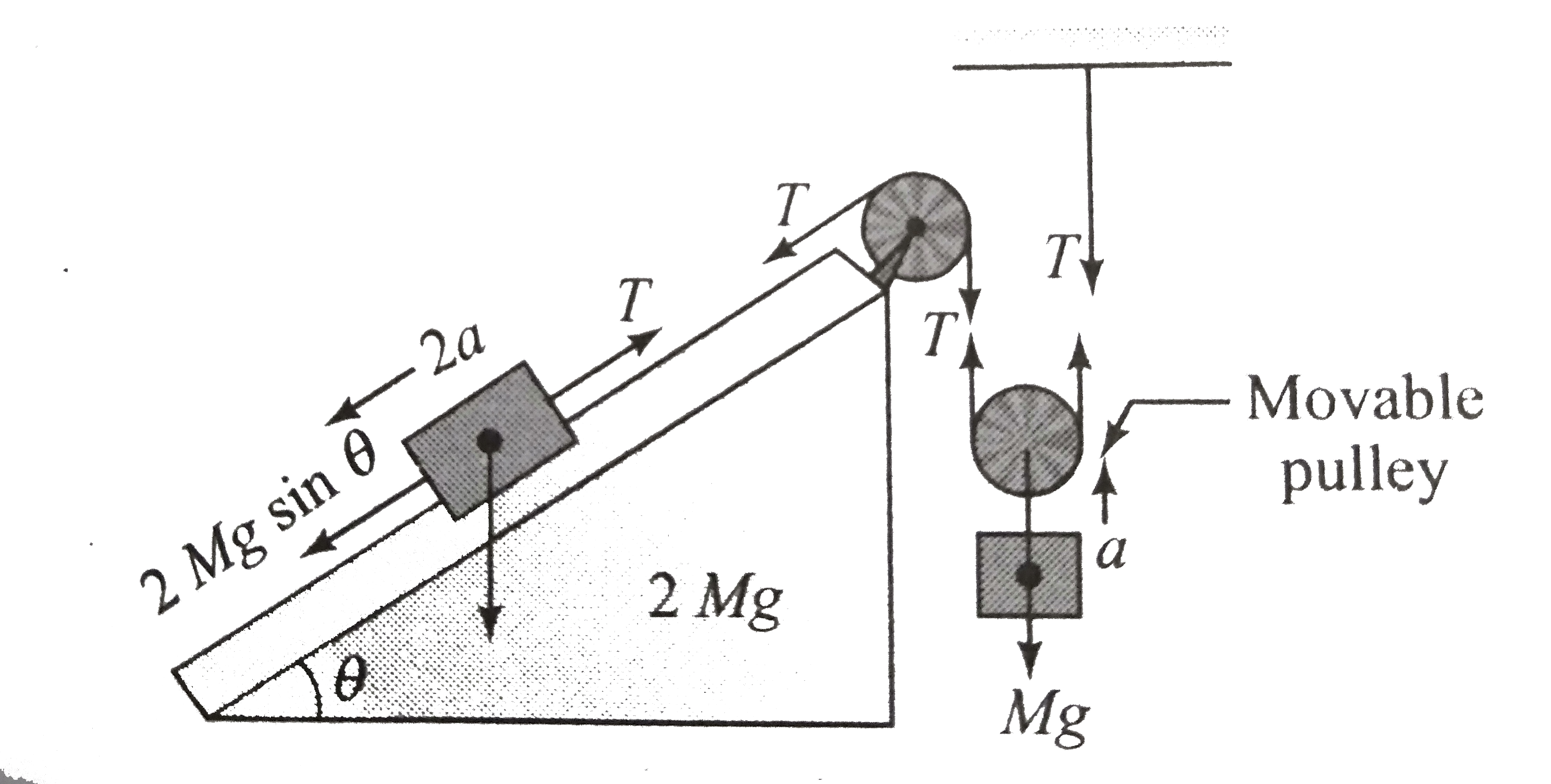
For block M,2T−Mg=Ma ...(ii)
Solving Eqs (i) and (ii), we get a=g[4sinθ−1]9.
Topper's Solved these Questions
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Exercise 6.4
13 Videos
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Subjective
15 Videos
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Exercise 6.2
35 Videos
- MISCELLANEOUS VOLUME 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 2EXERCISE - INTEGER_TYPE
10 Videos
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Integer type
1 Videos
Similar Questions
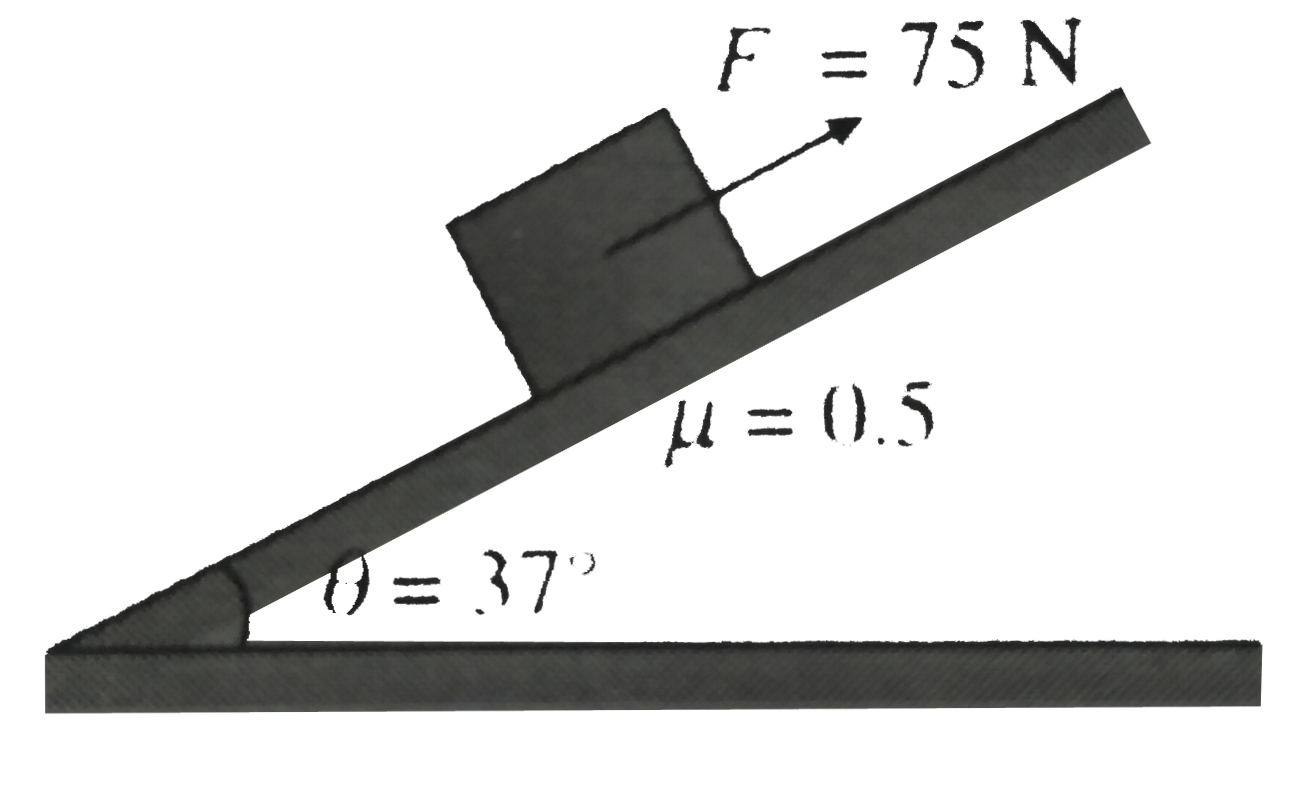
A block of mass M=10kg is placed inclined plane , inclined at angle θ=37∘ with horizontal The coefficient of friction between the block and inclined is μ=0.5
a. Calculate the acceleration of the block when it is released
b. Now a force F=75N is appling on block as shown find out the acceleration of the block If the block is initially at rest .
c. In case (b), how much force should be added to 75N force so that block the starts to move up the incline.
d. In case (b), what is the minimum force by which 75N force should be replaced with so that the block does not move?

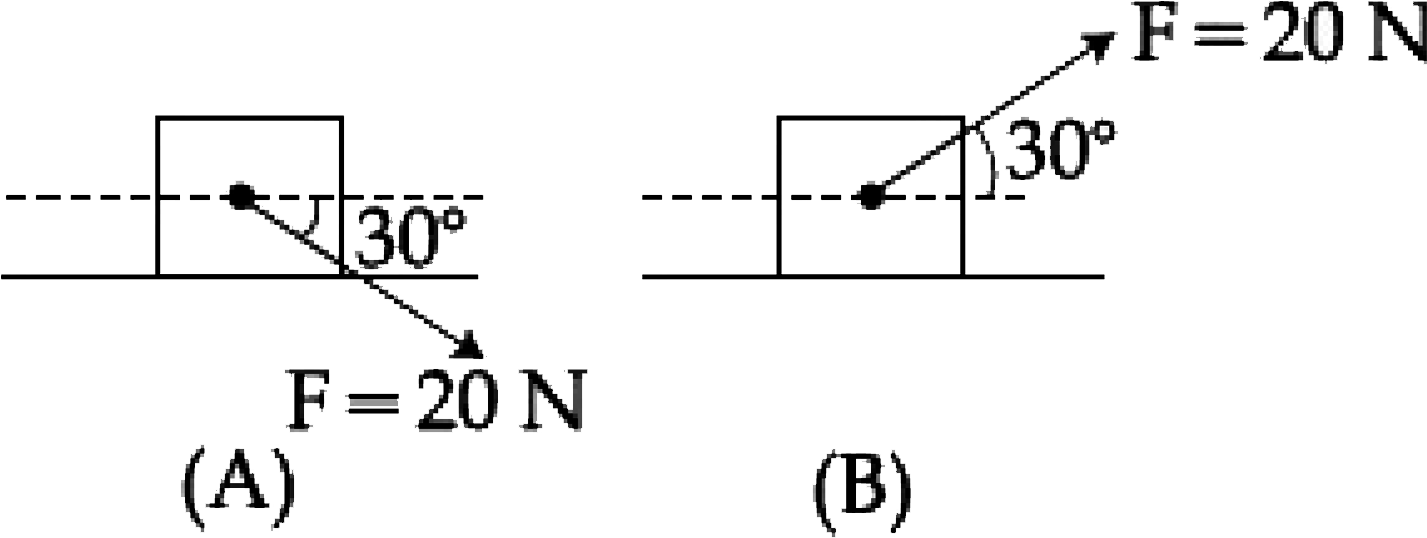
View SolutionA block of mass 5kg is (i) pushed in case (A) and (ii) pulled in case (B), by a force F=20N, making an angle of 30∘ with the horizontal, as shown in the figures. The coefficient of friction between the block and floor is μ=0.2. The difference between the accelerattion of the block, in case (B) and case (A) will be : (g=10ms−2).
 .
.
View SolutionThree blocks A, B, and C of masses 3M,2M, and M are suspended vertically with the help of spring PQ and TU, and a string RS as shown in fig. If the acceleration of blocks A, B and C is a1,a2 and a3 , respectively, then

The value of acceleration a1 at the moment string RS is cut is
View SolutionThree blocks A, B, and C of masses 3M,2M, and M are suspended vertically with the help of spring PQ and TU, and a string RS as shown in fig. If the acceleration of blocks A, B and C is a1,a2 and a3 , respectively, then

The value of acceleration a3 at the moment spring PQ is cut is
View SolutionThree blocks A, B, and C of masses 3M,2M, and M are suspended vertically with the help of spring PQ and TU, and a string RS as shown in fig. If the acceleration of blocks A, B and C is a1,a2 and a3 , respectively, then

The value of acceleration a2 at the moment spring TU is cut is
View SolutionFind the acceleration of block B as shown in fig. (a) and (b) relative to block A and relative to ground if block A is moving toward right with acceleration a.

View SolutionThree block A,B,and C of mass m1,m2 and m3, respectively are resting one on top of the other as shown in fig. A horizontal force F is applied on block B. Assuming all the surfaces are frictionless, calculate (1) acceleration of block A, block B, and block C, (2) normal reactions between A and B, B and C, and between C and ground .

View SolutionIn figures (a), (b) and (c) shown, the objects A, B and C are of same mass. String, spring and pulley are massless. C strikes B with velocity u in each case and sticks it. The ratio of velocity of B in case (a) to (b) to (c) is

View SolutionTwo blocks 'A' and 'B' having masses mA and ma, respectively are connectd by an arrangement shown in the figure. Calculate the downward acceleration of the block B. Assume the pulleys to be massless. Under what condition will block A have downward acceleration?

View SolutionIn figure calculate the linear acceleration of the blocks.
Mass of block B=8kg
mass of disc shaped pulley =2kg (take g=10m/s2)
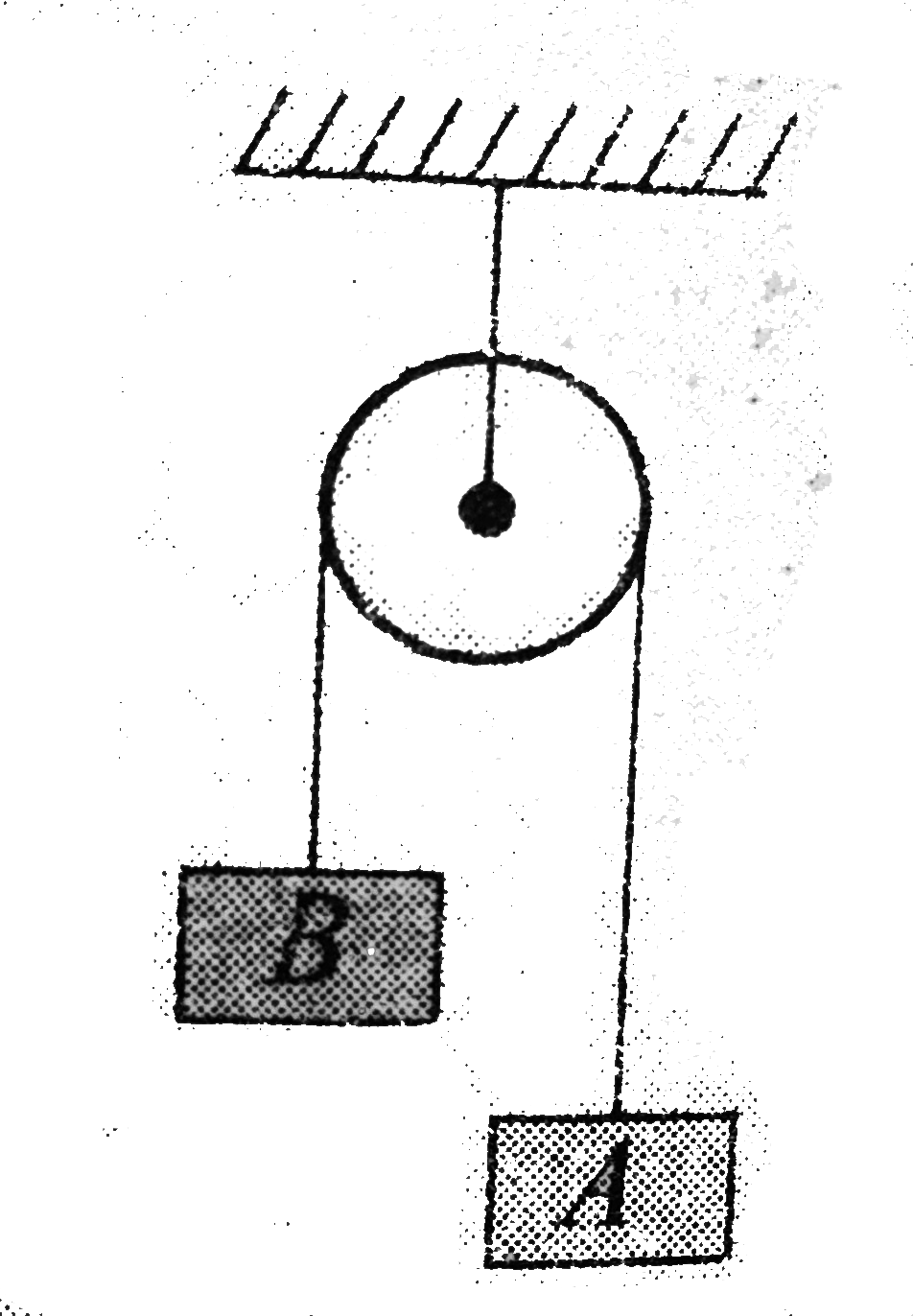
View Solution
