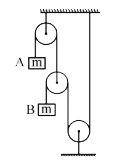
Two blocks 'A' and 'B' having masses mA and ma, respectively are connectd by an arrangement shown in the figure. Calculate the downward acceleration of the block B. Assume the pulleys to be massless. Under what condition will block A have downward acceleration?

According to Newton 2nd Law
mBg−T=mBaB (From FBD of mB) ...1
2T−mAg=mAaA (From FBD of mA) ...2
Constraint relation
aB=2aA=a ...3
Solving equation 1, 2 & 3
aB=a=2g(2mB−mA)(4mB+mA),aA=a2=g(2mB−mA)(4mB+mA).
Block A will have downward motion if aA<0⇒(2mB−mA)<0
⇒mA>2mB
Similar Questions
In the arrangement shown, the pulleys and strings are massless. The acceleration of block B is :
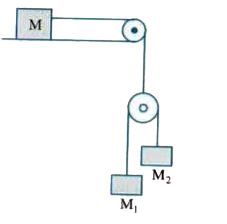
View SolutionReferring to figure calculate the downward acceleration of mass m1. Assume the surfaces are frictionless and pullyes are massless.
View SolutionIn the pulley-block arrangement shown in figure , find the relation between acceleration of blocks A and B

View SolutionIn the pulley-block arrangement shown in figure , find the relation between acceleration of blocks A and B

View SolutionTwo block of masses m1 and m2 are connected as shown in the figure. The acceleration of the block m2 is:

View Solution
Two blocks of masses m1 and m2 are connected as shown in the figure. The acceleration of the block m2 is :
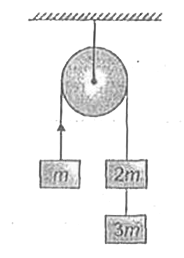
View SolutionIn the figure given below, with what acceleration does the block of mass m will move? (Pulley and strings are massless and frictionless)
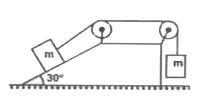
View SolutionTwo blocks, each having mass m, are connected with an ideal string through ideal pulleys on a frictionless fixed wedge as shown in the figure. The acceleration of the blocks is
View SolutionIn figure calculate the linear acceleration of the blocks.
Mass of block B=8kg
mass of disc shaped pulley =2kg (take g=10m/s2)
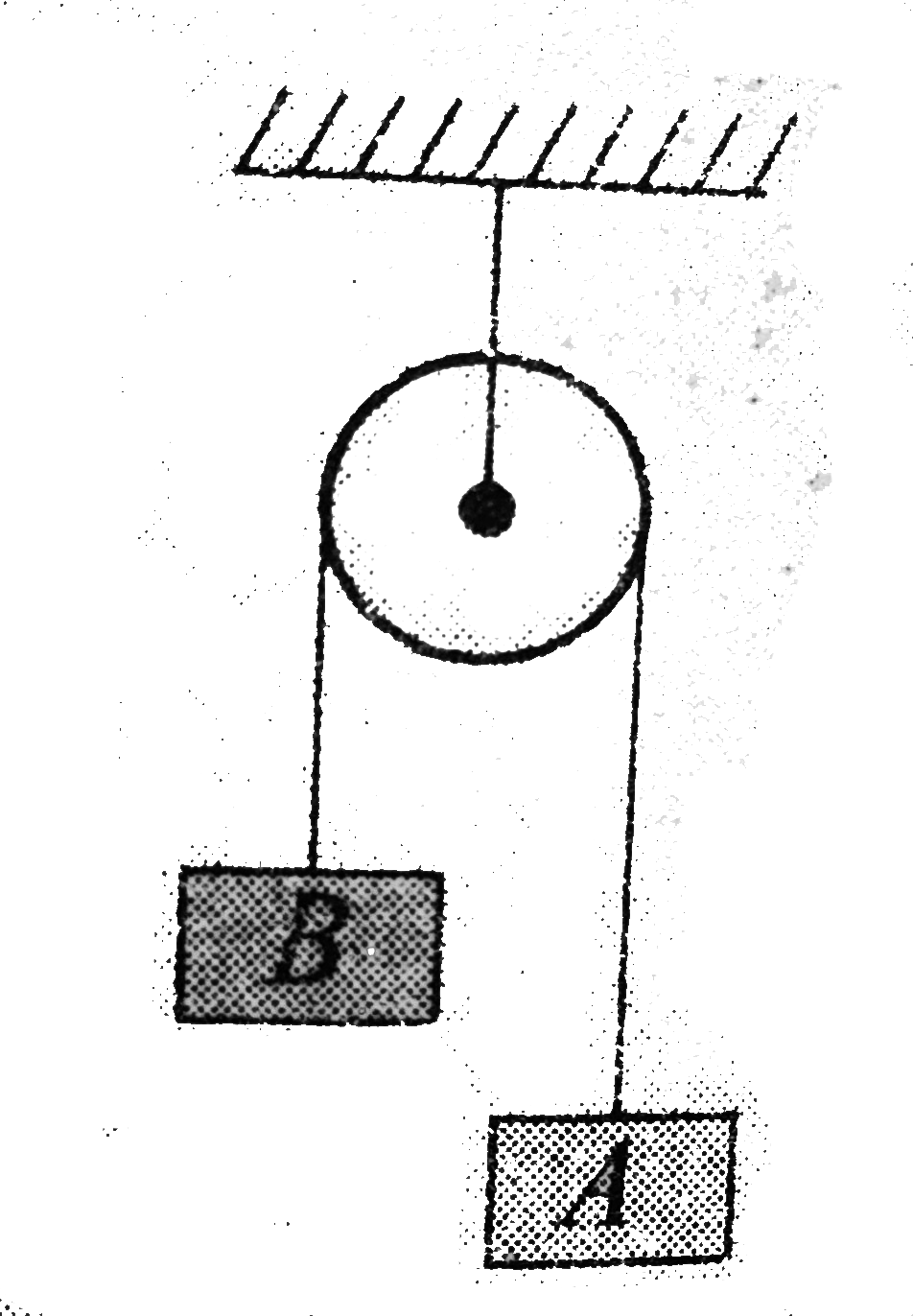
View SolutionFind the relation between acceleration of the two blocks m1andm2. Assume pulleys are massless and frictionless and the strings are inextensible .
View Solution
