A bomber plane moves due east at 100kmh−1 over a town T at a certain instant of time. Six minutes later, an interceptor plane sets off flying due north - east from the station S which is 40km south of T. If both maintain their courses, find the velocity with which the interceptor plane must fly in order to just overtake the bomber.
The correct Answer is:400√23kmh−1
Both should reach simultaneously at A.
TS=40km⇒TA=40km
Time taken by bomber to reach A :
t=40100=25h=24min
So time taken by interceptor plane to reach A :
24−6=18min,v=40√2(80/60)=400√23kmh−1.
 .
.
Related Playlists
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-2EXERCISE - Exercise Single Correct76videos
KINEMATICS-2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-2EXERCISE - Exercise Multiple Correct11videos
KINEMATICS-2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-2EXERCISE - Exercise 5.411videos
KINEMATICS-2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-1EXERCISE - Integer9videos
KINEMATICS-1
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASESEXERCISE - Compression2videos
KINETIC THEORY OF GASES
Similar Questions
An observer at an anti air craft post A identifies an enemy aircraft due East of his post at an angle of elevation of 60∘. At the same instant a detection post D 4kms south of A reports the aircraft at an elevation of 30∘. Calculate the altitude at which the plane is flying.
View SolutionAn aeroplane pilot wishes to fly due west A wind of 100kmh−1 is blowing towards south.
(a) If the speed of the plane (its speed in still air) is 300kmh−1 in which direction should the pilot head ?
(b) What is the speed of the plane with respect tom ground ? Illustrate with a vector diagram.View SolutionA plane moves in windy weather due east while the pilot the plane somewhat south of east. The wind is blowing at 50 km/h directed 30∘ east of north, while the palne moves at 200 km/h relative to the wind . What is the velocity of the plane relative to the ground and what is the direction in which the pilot points the palne ?
View SolutionAn aeroplane has to go from a point A to another point B, 500km away due 30∘ east of north. Wind is blowing due north at a speed of 20m/s. The air-speed of the plane is 150m/s. (a) Find the direction in which the pilot should head the plane to reach the point B. (b) Find the time taken by the plane to go from A to B.
View SolutionAn aeroplane has to go from a point P to another point Q, 1000 km away due north. Wind is blowing due east at a speed of 200km/h. The air speed of plane is 500km/h.
(a) Find the direction in which the pilot should head the plane to reach the point Q.
(b) Find the time taken by the plane to go from P to Q.View SolutionAn aeroplane has to go from a point O to another point A, at distance d due 37∘ East of North. A wind is blowing due North at a speed of 10ms−1. The air speed of the plane is v. (i) Find the direction in which the pilot should head the plane to reach the point A. (ii) Find the time taken by the plane to go from O to A.
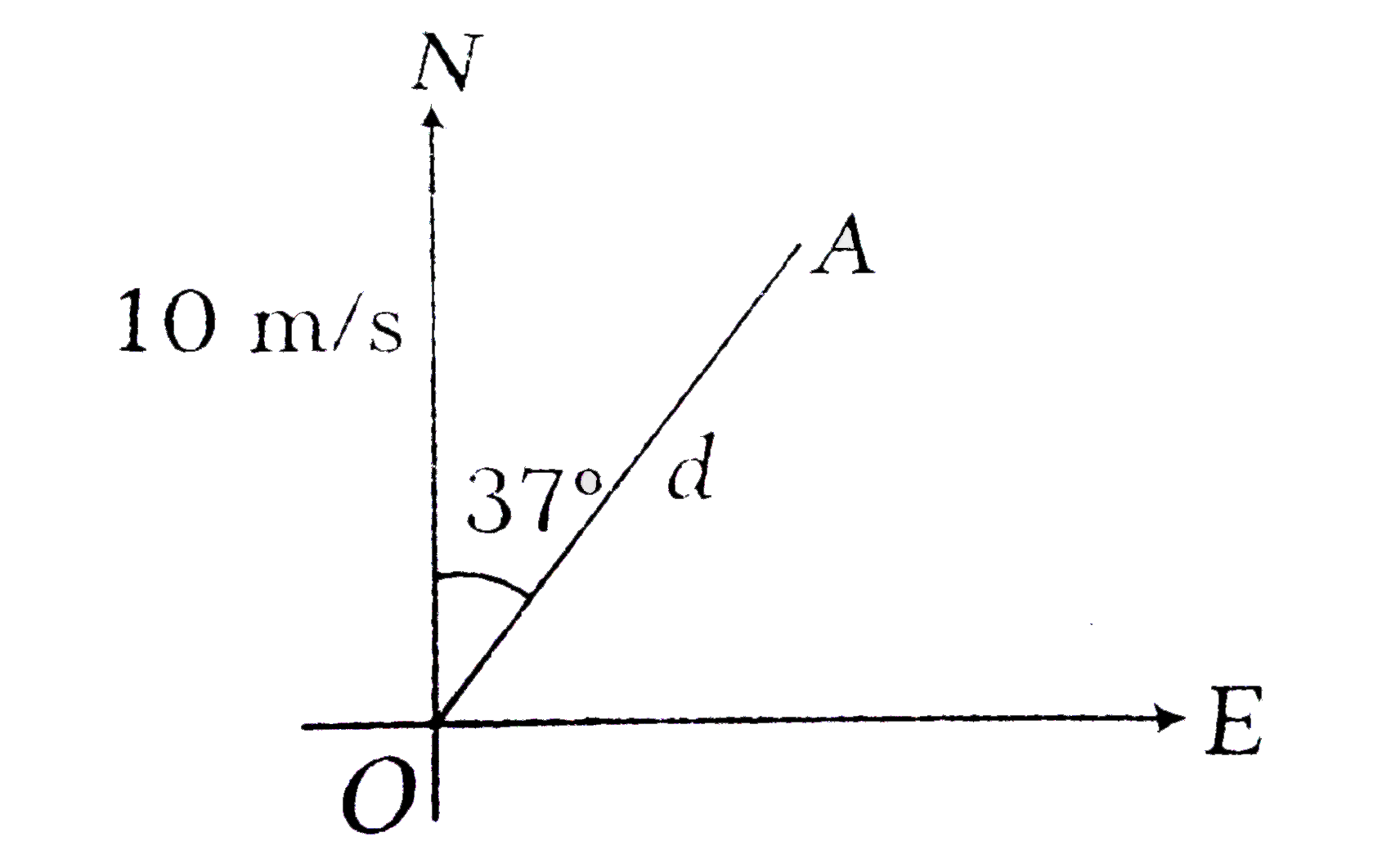 View Solution
View SolutionA student is running at her top speed of 5.0ms−1, to catch a bus, which is stopped at the bus stop. When the student is still 40.0m from the bus, it starts to pull away, moving with a constant acceleration of 0.2ms−2.
a For how much time and what distance does the student have to run at 5.0ms−1 before she overtakes the bus?
b. When she reached the bus, how fast was the bus travelling?
c. Sketch an x−t graph for bothe the student and the bus.
d. Teh equations uou used in part (a)to find the time have a second solution, corresponding to a later time for which the student and the bus are again at thesame place if they continue their specified motions. Explain the significance of this second solution. How fast is the bus travelling at this point?
e. If the students⊤speedis3.5 m s^(-1), will she catch the bus?
f. What is the minimum speed the student must have to just catch up with the bus?For what time and what distance dies she have to run in that case?View SolutionA pilot is supposed to fly a certain distance AB, due east from A→B and then due west from B→A. The velocity of plane is v and that of air is u. The time for the round trip is t0 in still air. Show that
(a) if the air velocity be due east or west, the time for round trip will be t1=t0(1−u2v2).
(b) if the air velocity is due north or south, the time for a round trip will be t2=t0√(1−u2v2).
 .View Solution
.View SolutionA fighter plane of length 20 m, wing span (distane from tip of one wing to the tip of the other wing) of 15 m and height 5 m is flying towards east over Delhi. It speed is 240ms1 . The earth’s magnetic field over Delhi is 5×10−5 T with the declination angle ~00 and dip of θ such that sin =(2)/(3). If the voltage developed is VB between the lower and upper side of the plane and VW between the tips of the wings then VB and VW are close to :
View SolutionA man of height H is standing in front of an inclined plane mirror at an angle θ from horizontal. The vertical separation between man and inclined plane is x. Man can see its complete image in length H(H+x)sinθH+2x of mirror .
(Given : x = H = 1m and θ=45∘)
_E01_112_Q01.png)
If man starts moving with velocity √2ms−1 along inclined plane, find out length of mirror at t = 1s in which he can see his complete image,View Solution


