A man of height H is standing in front of an inclined plane mirror at an angle θ from horizontal. The vertical separation between man and inclined plane is x. Man can see its complete image in length H(H+x)sinθH+2x of mirror .
(Given : x = H = 1m and θ=45∘)
_E01_112_Q01.png)
If man starts moving with velocity √2ms−1 along inclined plane, find out length of mirror at t = 1s in which he can see his complete image,
√23m
23
13m
13√2m
The correct Answer is:A
In this case x, H and θ remains same so required length of mirror = H(H+x)sinθH+2x
=1(1+1)sin45∘1+2×1=√23m
Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE - 04 (A)
47 Videos
- GEOMETRICAL OPTICSBOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE - 04 (B)
15 Videos
- GEOMETRICAL OPTICSBOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - ASSERTION-REASON
36 Videos
- CURRENT ELECTRICITYBOOK - ALLENCHAPTER - CURRENT ELECTRICITYEXERCISE - EX.II
66 Videos
- GRAVITATIONBOOK - ALLENCHAPTER - GRAVITATIONEXERCISE - EXERCISE 4
9 Videos
Similar Questions
A man of height H is standing in front of an inclined plane mirror at an angle θ from horizontal. The vertical separation between man and inclined plane is x. Man can see its complete image in length H(H+x)sinθH+2x of mirror .
(Given : x = H = 1m and θ=45∘)
_E01_113_Q01.png)
If man starts moving with velocity 1ms−1 along vertical, find out length of mirror at t = 1s in which he can see his complete image.
View SolutionA man of height H is standing in front of an inclined plane mirror at an angle θ from horizontal. The vertical separation between man and inclined plane is x. Man can see its complete image in length H(H+x)sinθH+2x of mirror .
(Given : x = H = 1m and θ=45∘)
_E01_114_Q01.png)
If man starts moving with velocity 1ms−1 horizontally, find out length of mirror at t=1s in which he can see his complete image.
View Solution
Knowledge Check
A man standing in front of a plane mirror finds his image to be at a distance of 6 metre from himself. The distance of man from the mirror is :
A6mB3mC2mD12m
A projectile is fired with a velocity v at right angle to the slope inclined at an angle θ with the horizontal. The range of the projectile along the inclined plane is
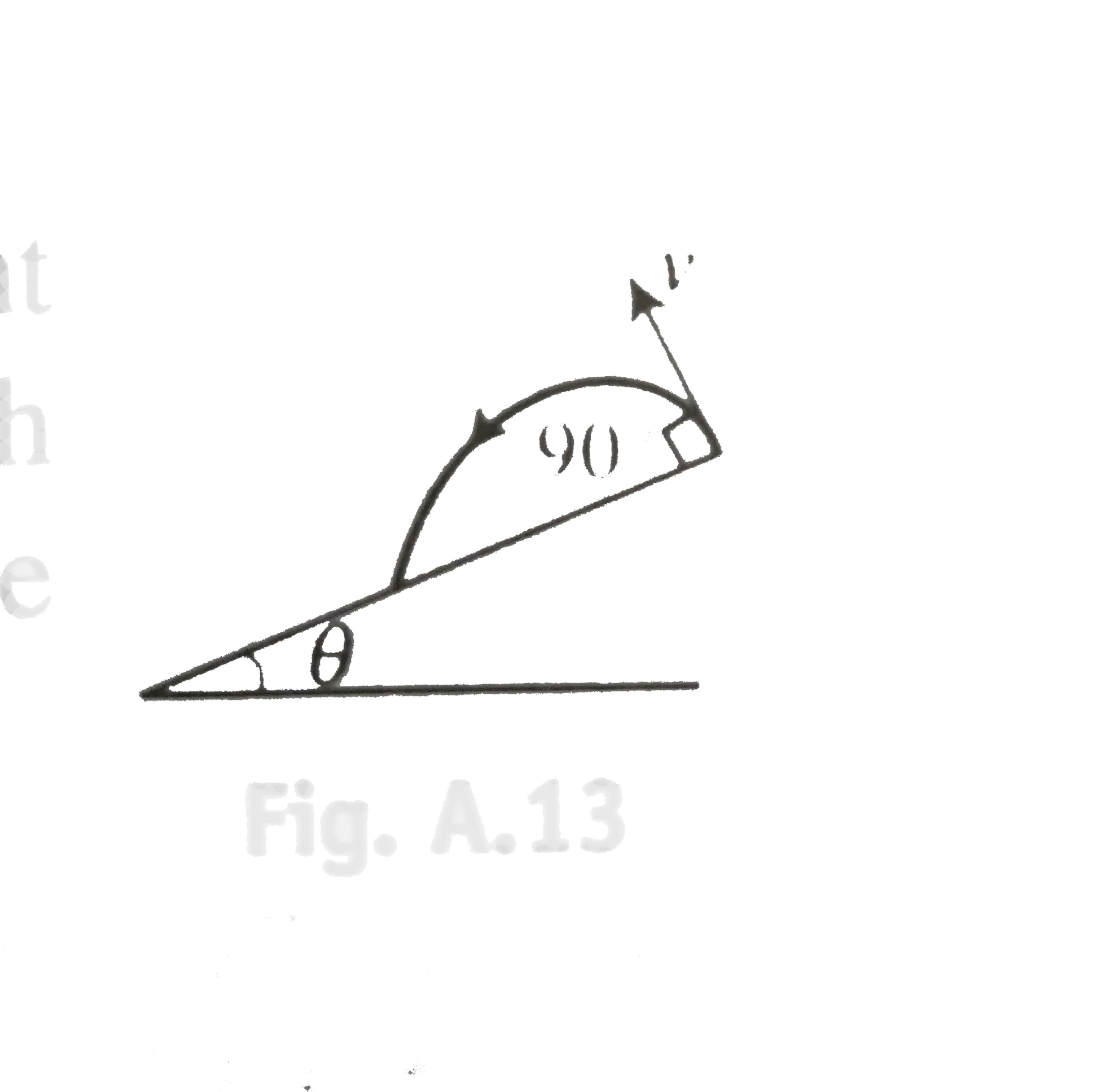
View SolutionA man standing in front of a plane mirror finds his image at a distance 6 metre from himself. What is the distance of man from the mirror?
View SolutionA man standing in front of a plane mirror finds his image at a distance 6 metre from himself. What is the distance of man from the mirror?
View SolutionA man goes 80 m on an inclined cliff inclined at 45∘ from the horizontal. Find the vertical height of the man from the ground.
View SolutionThe velocity of a sphere rolling down an inclined plane of height h at an inclination θ with the horizontal, will be :
View SolutionA man of length h requires a mirror of length at least equal to, to see his own complete image
View SolutionA block of mass m is placed on a rough plane inclined at an angle θ with the horizontal. The coefficient of friction between the block and inclined plane is μ . Ifθ<tan−1(μ) , then net contact force exerted by the plane on the block is :
View Solution
