An aeroplane pilot wishes to fly due west A wind of is blowing towards south.
(a) If the speed of the plane (its speed in still air) is in which direction should the pilot head ?
(b) What is the speed of the plane with respect tom ground ? Illustrate with a vector diagram.
south of west
East of north
north of west
none of these
The correct Answer is:c
To solve the problem step by step, we will break it down into two parts as given in the question.
Part (a): Direction in which the pilot should head
1. Identify the vectors involved:
- The velocity of the plane in still air (V_p) = 300 km/h (heading due west).
- The velocity of the wind (V_w) = 100 km/h (blowing towards south).
2. Draw the vector diagram:
- Draw a horizontal line pointing to the left to represent the westward direction (V_p).
- Draw a vertical line pointing downwards to represent the southward wind (V_w).
3. Determine the resultant vector:
- The pilot needs to adjust the heading to account for the wind. The effective velocity of the plane with respect to the ground (V_pg) can be represented as:
Vpg=Vp+(−Vw)
- This means we need to find the angle θ such that the resultant vector points directly west.
4. Use trigonometry to find the angle θ:
- In the right triangle formed by V_p and V_w, we can use the sine function:
sin(θ)=VwVp=100300=13
- Therefore,
θ=sin−1(13)
- This angle θ is north of west.
5. Conclusion for part (a):
- The pilot should head at an angle of sin−1(13) north of west.
Part (b): Speed of the plane with respect to the ground
1. Calculate the speed of the plane with respect to the ground:
- The speed of the plane with respect to the ground can be calculated using the cosine of the angle θ:
Vpg=Vp⋅cos(θ)
- We know:
cos(θ)=√1−sin2(θ)=√1−(13)2=√1−19=√89=2√23
2. Substituting the values:
- Now substituting back into the equation for V_pg:
Vpg=300⋅2√23=200√2 km/h
3. Conclusion for part (b):
- The speed of the plane with respect to the ground is 200√2 km/h.
Summary of the solution:
- Part (a): The pilot should head at an angle of sin−1(13) north of west.
- Part (b): The speed of the plane with respect to the ground is 200√2 km/h.
- The velocity of the plane in still air (V_p) = 300 km/h (heading due west).
- The velocity of the wind (V_w) = 100 km/h (blowing towards south).
- Draw a horizontal line pointing to the left to represent the westward direction (V_p).
- Draw a vertical line pointing downwards to represent the southward wind (V_w).
- The pilot needs to adjust the heading to account for the wind. The effective velocity of the plane with respect to the ground (V_pg) can be represented as:
Vpg=Vp+(−Vw)
- This means we need to find the angle θ such that the resultant vector points directly west.
- In the right triangle formed by V_p and V_w, we can use the sine function:
sin(θ)=VwVp=100300=13
- Therefore,
θ=sin−1(13)
- This angle θ is north of west.
- The pilot should head at an angle of sin−1(13) north of west.
- The speed of the plane with respect to the ground can be calculated using the cosine of the angle θ:
Vpg=Vp⋅cos(θ)
- We know:
cos(θ)=√1−sin2(θ)=√1−(13)2=√1−19=√89=2√23
- Now substituting back into the equation for V_pg:
Vpg=300⋅2√23=200√2 km/h
- The speed of the plane with respect to the ground is 200√2 km/h.
- Part (a): The pilot should head at an angle of sin−1(13) north of west.
- Part (b): The speed of the plane with respect to the ground is 200√2 km/h.
Topper's Solved these Questions
- INTRODUCTION TO VECTORS & FORCES Book:VMC MODULES ENGLISHChapter:INTRODUCTION TO VECTORS & FORCES Exercise:level 2
Explore 65 Videos
- INTRODUCTION TO VECTORS & FORCES Book:VMC MODULES ENGLISHChapter:INTRODUCTION TO VECTORS & FORCES Exercise:JEE Main ( ARCHIVE ) ( LEVEL-1)
Explore 12 Videos
- INTRODUCTION TO VECTORS & FORCES Book:VMC MODULES ENGLISHChapter:INTRODUCTION TO VECTORS & FORCES Exercise:JEE Advanced ( ARCHIVE LEVEL-2)
Explore 12 Videos
- GRAVITATIONBook:VMC MODULES ENGLISHChapter:GRAVITATIONExercise:JEE Advance (Archive) TRUE/FALSE
Explore 1 Video
- JEE MAIN - 5Book:VMC MODULES ENGLISHChapter:JEE MAIN - 5Exercise:PART I : PHYSICS (SECTION - 2)
Explore 5 Videos
Similar Questions
An aeroplane has to go from a point P to another point Q, 1000 km away due north. Wind is blowing due east at a speed of 200km/h. The air speed of plane is 500km/h.
(a) Find the direction in which the pilot should head the plane to reach the point Q.
(b) Find the time taken by the plane to go from P to Q.
View SolutionA jet airplane travelling at the speed of 500km−1 ejects its products of combustion at the speed of 1500kmh−1 relative to the jet plane. What is the speed of the burnt gases with respect to observer on the ground ?
View Solution
Knowledge Check
A jet airplane travelling at the speed of 500km−1 ejects its products of combustion at the speed of 1500kmh−1 relative to the jet plane. What is the speed of the burnt gases with respect to observer on the ground ?
A500kmh−1B1000kmh−1C1500kmh−1D2000kmh−1
A boat man can row with a speed of 10kmh−1 in still water. If the river flows steadily at 5km/h, in which direction should the boatman row in order to reach a point on the other bank directly opposite to the point from where he stared ? The width of the river is 2km.
View SolutionAn aeroplane has to go from a point A to another point B, 500km away due 30∘ east of north. Wind is blowing due north at a speed of 20m/s. The air-speed of the plane is 150m/s. (a) Find the direction in which the pilot should head the plane to reach the point B. (b) Find the time taken by the plane to go from A to B.
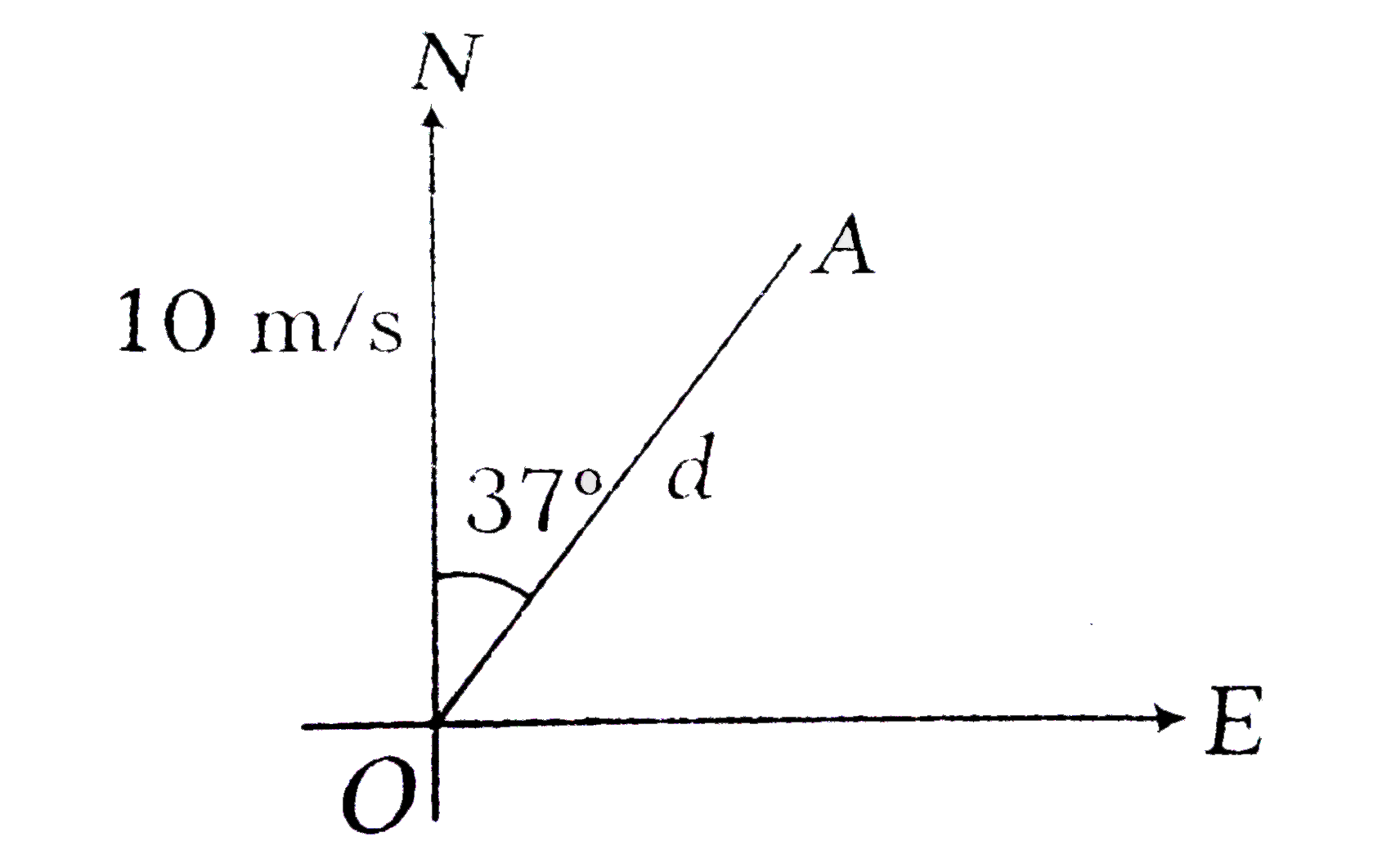
View SolutionAn aeroplane has to go from a point O to another point A, at distance d due 37∘ East of North. A wind is blowing due North at a speed of 10ms−1. The air speed of the plane is v. (i) Find the direction in which the pilot should head the plane to reach the point A. (ii) Find the time taken by the plane to go from O to A.
View SolutionA man swims across a river with speed of 5kmh−1 ( in still water). While a boat goes upstream with speed 12kmh−1 ( in still water). How fast and in which direction does, the man appear to go to the boatman ? Given that the speed of flowing water is 2kmh−1
View SolutionAn aircraft executes a horizontal loop at a speed of 720kmh−1, with its wings banked at 15∘ What is the radius of the loop ?
View SolutionAn aircraft executes a horizontal loop at a speed of 720kmh−1 , with its wings banked at 15∘ What is the radiue of the loop ?
View Solutionman wants to swim across a river of which 200 m along the shortest path . If the speed of river stream is 3kmh−1 and speed of swimmer in still water is 5kmh−1 , then the time of crossing the river is
View Solution