Projection of →P on →Q is :
→P.ˆQ
→P.ˆQ
→P׈Q
→P׈Q
The correct Answer is:a
To find the projection of vector P on vector Q, we can follow these steps:
1. Understand the Concept of Projection:
The projection of one vector onto another is a measure of how much of the first vector lies in the direction of the second vector. In this case, we want to find the projection of vector P onto vector Q.
2. Use the Projection Formula:
The formula for the projection of vector P onto vector Q is given by:
\text{Projection of } \overset{\rarr}{P} \text{ on } \overset{\rarr}{Q} = \frac{\overset{\rarr}{P} \cdot \overset{\rarr}{Q}}{|\overset{\rarr}{Q}|^2} \overset{\rarr}{Q}
where \overset{\rarr}{P} \cdot \overset{\rarr}{Q} is the dot product of vectors P and Q, and |\overset{\rarr}{Q}| is the magnitude of vector Q.
3. Express the Projection in Terms of Unit Vector:
The unit vector in the direction of Q is given by:
\overset{\rarr}{Q}_{\text{cap}} = \frac{\overset{\rarr}{Q}}{|\overset{\rarr}{Q}|}
Therefore, we can rewrite the projection as:
\text{Projection of } \overset{\rarr}{P} \text{ on } \overset{\rarr}{Q} = \overset{\rarr}{P} \cdot \overset{\rarr}{Q}_{\text{cap}}
4. Final Expression:
Thus, the projection of vector P on vector Q can be simplified to:
\text{Projection of } \overset{\rarr}{P} \text{ on } \overset{\rarr}{Q} = \overset{\rarr}{P} \cdot \overset{\rarr}{Q}_{\text{cap}}
Conclusion:
The projection of vector P on vector Q is given by the dot product of P with the unit vector of Q:
\text{Projection of } \overset{\rarr}{P} \text{ on } \overset{\rarr}{Q} = \overset{\rarr}{P} \cdot \overset{\rarr}{Q}_{\text{cap}}
The projection of one vector onto another is a measure of how much of the first vector lies in the direction of the second vector. In this case, we want to find the projection of vector P onto vector Q.
The formula for the projection of vector P onto vector Q is given by:
\text{Projection of } \overset{\rarr}{P} \text{ on } \overset{\rarr}{Q} = \frac{\overset{\rarr}{P} \cdot \overset{\rarr}{Q}}{|\overset{\rarr}{Q}|^2} \overset{\rarr}{Q}
where \overset{\rarr}{P} \cdot \overset{\rarr}{Q} is the dot product of vectors P and Q, and |\overset{\rarr}{Q}| is the magnitude of vector Q.
The unit vector in the direction of Q is given by:
\overset{\rarr}{Q}_{\text{cap}} = \frac{\overset{\rarr}{Q}}{|\overset{\rarr}{Q}|}
Therefore, we can rewrite the projection as:
\text{Projection of } \overset{\rarr}{P} \text{ on } \overset{\rarr}{Q} = \overset{\rarr}{P} \cdot \overset{\rarr}{Q}_{\text{cap}}
Thus, the projection of vector P on vector Q can be simplified to:
\text{Projection of } \overset{\rarr}{P} \text{ on } \overset{\rarr}{Q} = \overset{\rarr}{P} \cdot \overset{\rarr}{Q}_{\text{cap}}
The projection of vector P on vector Q is given by the dot product of P with the unit vector of Q:
\text{Projection of } \overset{\rarr}{P} \text{ on } \overset{\rarr}{Q} = \overset{\rarr}{P} \cdot \overset{\rarr}{Q}_{\text{cap}}
Topper's Solved these Questions
- INTRODUCTION TO VECTORS & FORCES Book:VMC MODULES ENGLISHChapter:INTRODUCTION TO VECTORS & FORCES Exercise:level 2
Explore 65 Videos
- INTRODUCTION TO VECTORS & FORCES Book:VMC MODULES ENGLISHChapter:INTRODUCTION TO VECTORS & FORCES Exercise:JEE Main ( ARCHIVE ) ( LEVEL-1)
Explore 12 Videos
- INTRODUCTION TO VECTORS & FORCES Book:VMC MODULES ENGLISHChapter:INTRODUCTION TO VECTORS & FORCES Exercise:JEE Advanced ( ARCHIVE LEVEL-2)
Explore 12 Videos
- GRAVITATIONBook:VMC MODULES ENGLISHChapter:GRAVITATIONExercise:JEE Advance (Archive) TRUE/FALSE
Explore 1 Video
- JEE MAIN - 5Book:VMC MODULES ENGLISHChapter:JEE MAIN - 5Exercise:PART I : PHYSICS (SECTION - 2)
Explore 5 Videos
Similar Questions
If →A=2ˆi+3ˆj−ˆk and →B=−ˆi+3ˆj+4ˆk and then projection of →A on →B will be :
View SolutionAre the magnitude and direction of →A−→B same as that →B−→A?
View SolutionDot product of two vectors →A and →B is defined as →A.→B=ABcosϕ , where ϕ is angle between them when they are drawn with tails coinciding. For any two vectors . This means ovsert(→)A.→B=→B.→A that . The scalar product obeys the commutative law of multiplication, the order of the two vectors does not matter. The vector product of two vectors →A and →B also called the cross product, is denoted by →A×→B . As the name suggests, the vector product is itself a vector. →C=→A×→B then C=ABsinθ ,
For non zero vectors →A,→B,→C,∣∣(→A×→B).→C∣∣=∣∣→A∣∣∣∣→B∣∣∣∣→C∣∣ holds if and only if
View SolutionDot product of two vectors →A and →B is defined as →A.→B=aBcosϕ , where ϕ is angle between them when they are drawn with tails coinciding. For any two vectors . This means →A.→B=→B.→A that . The scalar product obeys the commutative law of multiplication, the order of the two vectors does not matter. The vector product of two vectors →A and →B also called the cross product, is denoted by →A×→B . As the name suggests, the vector product is itself a vector. →C=→A×→B then C=ABsinθ ,
→A=ˆi+ˆj−ˆk and →B=2ˆi+3ˆj+5ˆk angle between →A and →B is
View SolutionDot product of two vectors →A and →B is defined as →A.→B=aBcosϕ , where ϕ is angle between them when they are drawn with tails coinciding. For any two vectors . This means →A.→B=→B.→A that . The scalar product obeys the commutative law of multiplication, the order of the two vectors does not matter. The vector product of two vectors →A and →B also called the cross product, is denoted by →A×→B . As the name suggests, the vector product is itself a vector. →C=→A×→B then C=ABsinθ ,
A force →F=3ˆi+cˆj+2ˆk acting on a particle causes a displacement d=4ˆi−2ˆj+3ˆk . If the work done (dot product of force and displacement) is 6J then the value of c is :
View SolutionThree vectors →P,→Q and →R are shown in the figure. Let S be any point on the vector →R The distance between the point P and S is ∣∣→R∣∣ . The general relation among vectors →P,→Q and →S is :
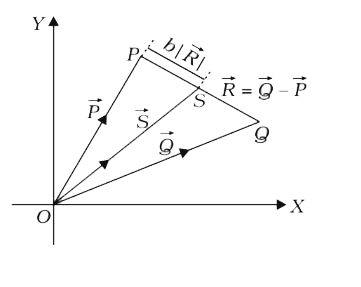
View SolutionIf →A+→B+→C =0 and A = B + C, the angle between →A and →B is :
View SolutionThe maqunitudes of vecotr →A,→B and →C are respectively 12,5 and 13 units and →A+→B=→C then the angle between →A and →B is :
View SolutionThe magnitude of the vector product of two vectors and may be : →A and →B
View SolutionThe angle between vector (→A×→B) and (→B×→A) is :
View Solution

