A river flows due south with a speed of 2.0ms−1. A man strees a motorboat across the river , his velocity relative to the water is 4ms−1 due east. The river is 800m wide.
(a) What is his velocity (magnitude and direction) relative to the earth ?
(b) How much time is required to cross the river ?
( c) HOw far south of his starting points will he reach the opposite bank ?
Velocity of river(i.e., speed of river w.r.t earth),
|→vr|=2ms−1
velocity of boat w.r.t. river, ∣∣→vb/r∣∣=4ms−1
Width of river =800m
Velocity of boat w.r.t. earth →vb=?
According to the given statement, the diagram will be as given in (Fig ).
(a) When two vectorc are acting at angle of 90∘, their resultant can be obtained by pythagorous theorem,
vb=√v2b,r+v2r=√16+4=√20=45ms−1
To find direction, we have
tanθ=vrvb,r=24=12⇒θ=tan−1(12)
(b) Time taken to cross the river is
(Displacement)/velocity of boat w.r.t. river)
velocity of boat w.r.t. river is used since it is the velocity with which the river is crossed.
So the boat will sross in 8004=200s
( c) The desired position on other side is A, but due to the current of river, boat is drifted to position B. To find out this drift, we need time taken in all to cross the river (200s) and speed of current (2ms−1).
So the distance AB = Time taken xx speed of current
=200×2=400m
Hence, the boat is drifted by 400m away from position A.
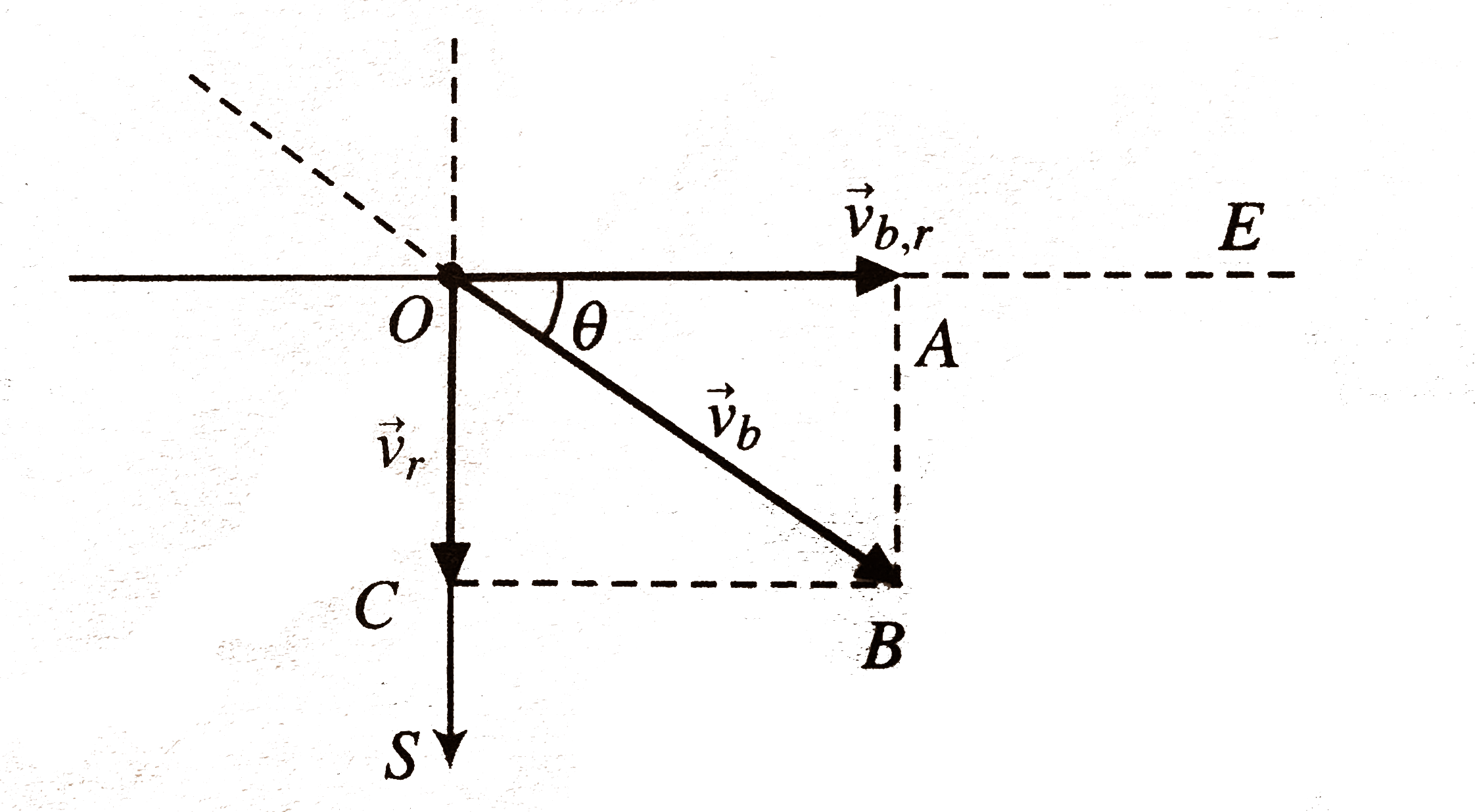 .
.
Topper's Solved these Questions
- KINEMATICS-2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-2EXERCISE - Solved Examples
7 Videos
- KINEMATICS-2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-2EXERCISE - Exercise 5.1
15 Videos
- KINEMATICS-1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-1EXERCISE - Integer
9 Videos
- KINETIC THEORY OF GASESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASESEXERCISE - Compression
2 Videos
Similar Questions
A swimmer wants to cross a 200 m wide river which is flowing at a speed of 2 m/s. the velocity of the swimmer with respect to the river is 1 m/s. how far from the point directly opposite to the starting point does the swimmer reach the opposite bank ?
View SolutionA river is flowing towards with a velocity of 5ms−1. The boat velocity is 10ms−1. The boat crosses the river by shortest path. Hence,
View SolutionA river is flowing towards with a velocity of 5ms−1. The boat velocity is 10ms−1. The boat crosses the river by shortest path. Hence,
View SolutionWidth of a river is 30m, velocity is 2m/s and rowing velocity is 5m/s at 37∘ from the direction of river current (a) find the time taken to cross the river, (b) drift of the boatman while reaching the other shore.
View SolutionAn aeroplane is flying with a velocity 800kmph relative to air wind is belong from west to east with a velocity 15ms−1. Find velocity of aeroplane relative to the earth to fly south ward
View SolutionA person reaches on a point directly opposite on the other bank of a river.The velocity of the water in the river is 4m/sand the velocity of the person in still water is 5m/s.If the width of the river is 84.6m, time taken to cross the river in seconds is
View SolutionA river is 20m wide. River speed is 3m/s. A boat starts with velocity 2√2m/s at angle 45∘ from the river current (relative to river)
(a) Find the time taken by the boat to reach the opposite bank.
(b) How far from the point directly opposite to the starting point does the boat reach the opposite bank?
View SolutionBoat moves with velocity 5 m/s on still water. It is steered perpendicular to the river current.
(a) Will it reach point B or somewhere else on the other bank ?
(b) How long will it take to cross the river?
(c) How far down stream, will it reach the other bank ?
(d) Does it take minimum time in this way ?
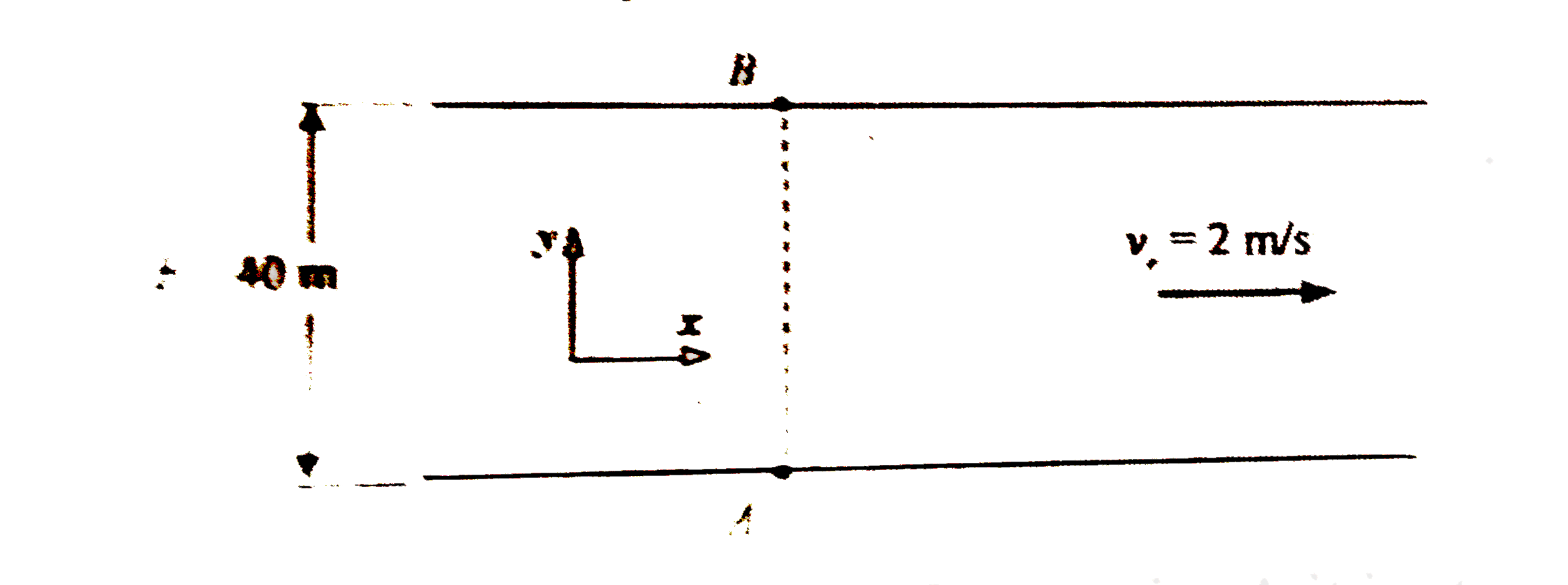
View SolutionA man desires to swim across the river in shortest time. The velcoity of river water is 3kmh−1 . He can swim in still water at 6kmh−1 . At what angle with the velocity of flow of the river should he swim ?
View SolutionA river is flowing due east with a speed 3ms−1 A swimmer can swim in still water at a speed of 4ms−1 If swimmer starts swimming due north what will be his resultant velocity (magnitude and direction )?
View Solution