A river is flowing due east with a speed 3ms−1 A swimmer can swim in still water at a speed of 4ms−1 If swimmer starts swimming due north what will be his resultant velocity (magnitude and direction )?
To solve the problem, we need to find the resultant velocity of the swimmer who is swimming north while the river flows east. We will use vector addition to find the magnitude and direction of the resultant velocity.
1. Identify the velocities:
- Velocity of the river (V_river) = 3 m/s (due east)
- Velocity of the swimmer (V_swimmer) = 4 m/s (due north)
2. Represent the velocities as vectors:
- V_river can be represented as a vector: →Vriver=3^i (where ^i is the unit vector in the east direction).
- V_swimmer can be represented as a vector: →Vswimmer=4^j (where ^j is the unit vector in the north direction).
3. Calculate the resultant velocity:
- The resultant velocity →Vresultant can be found using vector addition:
→Vresultant=→Vriver+→Vswimmer=3^i+4^j
4. Find the magnitude of the resultant velocity:
- The magnitude of the resultant velocity can be calculated using the Pythagorean theorem:
Vresultant=√(Vriver)2+(Vswimmer)2=√(3)2+(4)2=√9+16=√25=5m/s
5. Determine the direction of the resultant velocity:
- To find the angle θ with respect to the north direction, we can use the tangent function:
tan(θ)=VriverVswimmer=34
- Therefore, θ=tan−1(34).
- Calculating θ:
θ≈36.87∘
6. State the final answer:
- The resultant velocity of the swimmer is 5m/s at an angle of approximately 36.87∘ east of north.
Final Answer:
- Magnitude of resultant velocity: 5 m/s
- Direction of resultant velocity: 36.87° east of north
- Velocity of the river (V_river) = 3 m/s (due east)
- Velocity of the swimmer (V_swimmer) = 4 m/s (due north)
- V_river can be represented as a vector: →Vriver=3^i (where ^i is the unit vector in the east direction).
- V_swimmer can be represented as a vector: →Vswimmer=4^j (where ^j is the unit vector in the north direction).
- The resultant velocity →Vresultant can be found using vector addition:
→Vresultant=→Vriver+→Vswimmer=3^i+4^j
- The magnitude of the resultant velocity can be calculated using the Pythagorean theorem:
Vresultant=√(Vriver)2+(Vswimmer)2=√(3)2+(4)2=√9+16=√25=5m/s
- To find the angle θ with respect to the north direction, we can use the tangent function:
tan(θ)=VriverVswimmer=34
- Therefore, θ=tan−1(34).
- Calculating θ:
θ≈36.87∘
- The resultant velocity of the swimmer is 5m/s at an angle of approximately 36.87∘ east of north.
- Magnitude of resultant velocity: 5 m/s
- Direction of resultant velocity: 36.87° east of north
Topper's Solved these Questions
- INTRODUCTION TO VECTORS & FORCES Book:VMC MODULES ENGLISHChapter:INTRODUCTION TO VECTORS & FORCES Exercise:level 1
Explore 75 Videos
- INTRODUCTION TO VECTORS & FORCES Book:VMC MODULES ENGLISHChapter:INTRODUCTION TO VECTORS & FORCES Exercise:level 2
Explore 65 Videos
- GRAVITATIONBook:VMC MODULES ENGLISHChapter:GRAVITATIONExercise:JEE Advance (Archive) TRUE/FALSE
Explore 1 Video
- JEE MAIN - 5Book:VMC MODULES ENGLISHChapter:JEE MAIN - 5Exercise:PART I : PHYSICS (SECTION - 2)
Explore 5 Videos
Similar Questions
A river is flowing due east with a speed 3m/s (Fig. 2 (EP) .31 ).
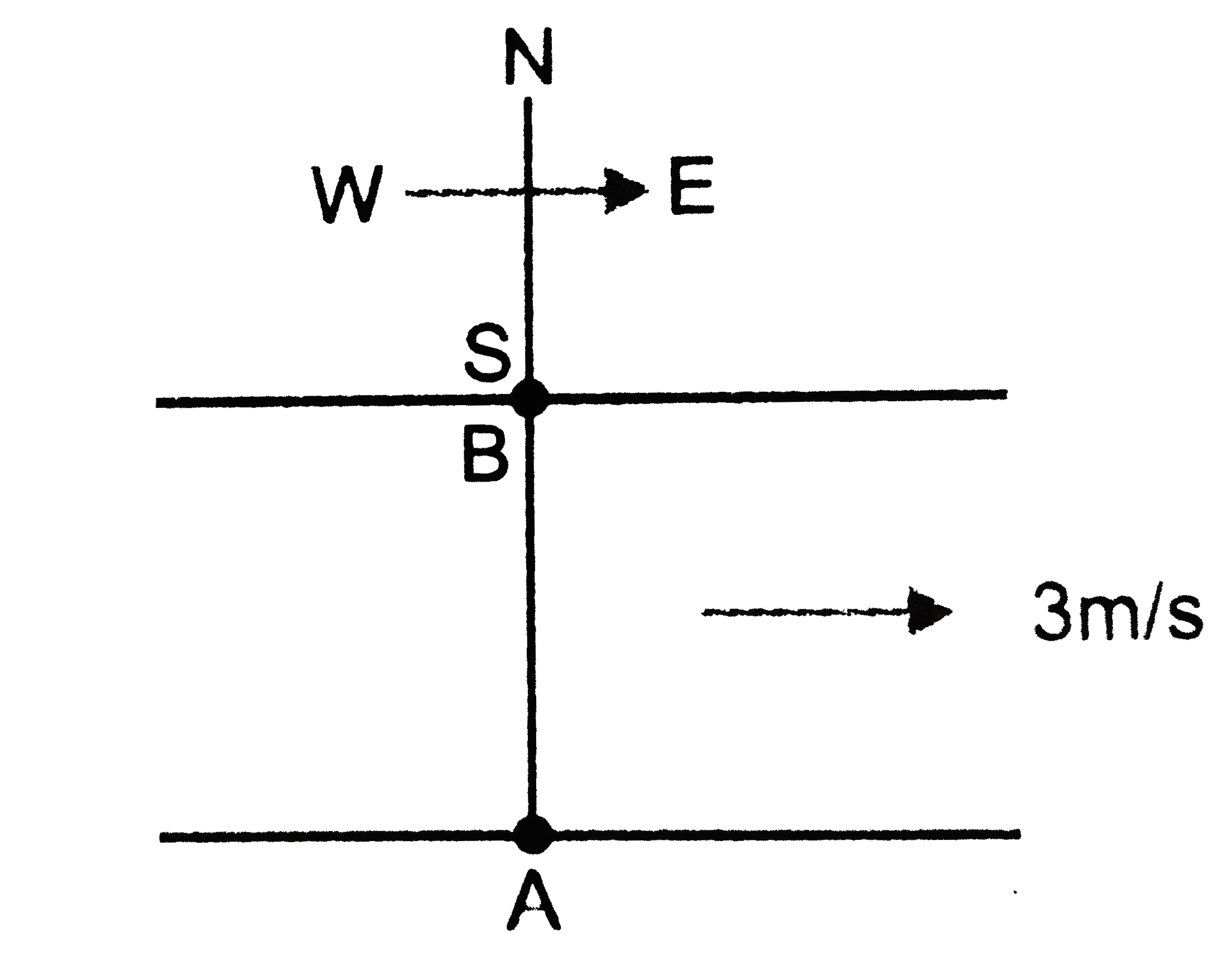 . (a) If swimmer starts swimming due north, what will be his resultant velocity (magnitude and direction) ? (b) If he wants to start from point (A) on South bank and reach opposite point (B) on North bank,
. (a) If swimmer starts swimming due north, what will be his resultant velocity (magnitude and direction) ? (b) If he wants to start from point (A) on South bank and reach opposite point (B) on North bank,
(i) Which direction should he swim? (ii) What will be his resultant speed ? (c ) From two differenrent casses as mentioned in (a) and 9b) above, in which casse will he reach opposite bank in shorter time ?
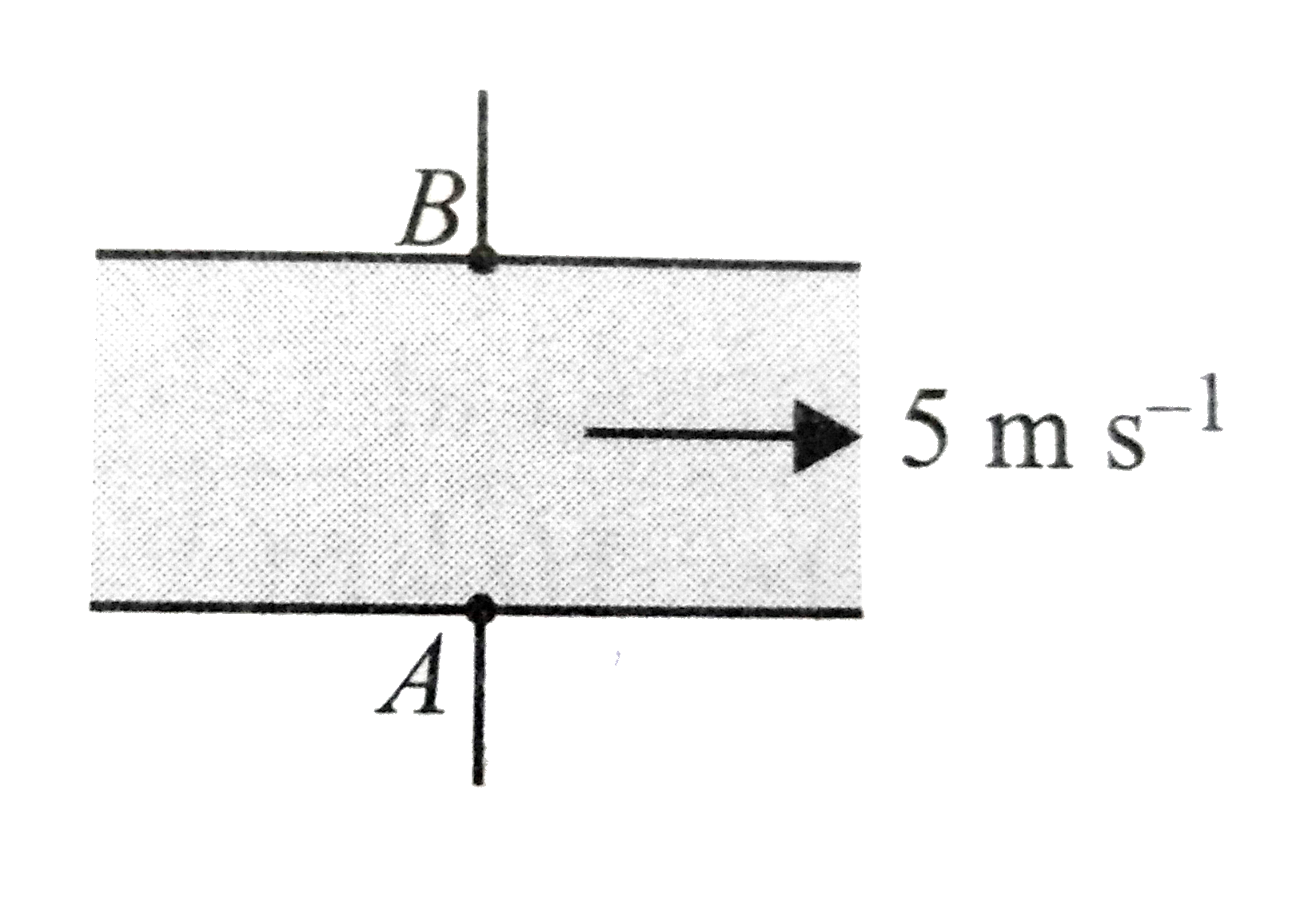
View SolutionA river is flowing from west to east with a speed 5m/s. A swimmer can swim in still water at a speed of 10m/s .
If he wants to start from point A on south bank and reach opposite point B on north bank. In what direction direction should he swim ?
View Solution
Knowledge Check
A river is flowing due east with a speed 3ms−1. A swimmer can swim in still water at a speed of 4ms−1. If swimmer starts swimming due north, then the resultant velocity of the swimmer is a) 3 m/s b) 5 m/s c) 7 m/s d) 2 m/s
A3 m s−1B5 m s−1C7 m s−1D2 m s−1
A swimmer can swim in still water with a speed of 2.5 m/s. What is the shortest time taken by him to swim across the river?

View SolutionA river is flowing from west to east with a speed of 5m/min. A man can swim in still water with a velocity 10m/min. In which direction should the man swim so as to take the shortest possible path to go to the south.
View SolutionA river flows due south with a speed of 2.0ms−1. A man strees a motorboat across the river , his velocity relative to the water is 4ms−1 due east. The river is 800m wide.
(a) What is his velocity (magnitude and direction) relative to the earth ?
(b) How much time is required to cross the river ?
( c) HOw far south of his starting points will he reach the opposite bank ?
View SolutionAn aeroplane is heading north east at a speed of 141.4 ms−1 . The northward component of its velocity is
View SolutionA bird is fying due east with a velocity of 4ms−1. The starts to blow with a velocity of 3ms−1 due north. What is the magnituide of relative velocity of bird w.r.t. wind ? Find out its direction also.
View SolutionA river is of width 120m which flows at a speed pf 8ms−1. If a man swims with a speed of 5ms−1 at an angle of 127∘ with the stream, his drift on reaching other bank is
View SolutionA river is flowing at the rate of 6 km/hr. A swimmer swims across with a velocity of 9 km/hr w.r.t. water. The resultant velocity of the man will be in (km/hr):-
View Solution