A block of mass 0.1 is held against a wall applying a horizontal force of 5N on block. If the coefficient of friction between the block and the wall is 0.5, the magnitude of the frictional force acting on the block is:
2.5 N
0.98 N
4.9 N
0.49 N
The correct Answer is:b
To solve the problem, we need to find the magnitude of the frictional force acting on a block of mass 0.1 kg that is held against a wall with a horizontal force of 5 N applied to it. The coefficient of friction between the block and the wall is 0.5.
1. Identify the Forces Acting on the Block:
- The block experiences a horizontal force F=5N applied against the wall.
- The weight of the block W=mg, where m=0.1kg and g=9.8m/s2.
- The normal force N exerted by the wall on the block.
- The frictional force f acting opposite to the direction of the applied force.
2. Calculate the Weight of the Block:
W=mg=0.1kg×9.8m/s2=0.98N
3. Determine the Maximum Static Friction Force:
The maximum static friction force fmaxs can be calculated using the formula:
fmaxs=μsN
where μs=0.5 is the coefficient of friction.
4. Calculate the Normal Force:
Since the block is in equilibrium vertically, the normal force N is equal to the weight of the block:
N=W=0.98N
5. Calculate the Maximum Static Friction Force:
fmaxs=μsN=0.5×0.98N=0.49N
6. Determine the Frictional Force:
The frictional force f will adjust to prevent the block from sliding down. Since the applied force F=5N is greater than the maximum static friction force fmaxs=0.49N, the frictional force will be equal to its maximum value:
f=fmaxs=0.49N
Final Answer:
The magnitude of the frictional force acting on the block is 0.49N.
- The block experiences a horizontal force F=5N applied against the wall.
- The weight of the block W=mg, where m=0.1kg and g=9.8m/s2.
- The normal force N exerted by the wall on the block.
- The frictional force f acting opposite to the direction of the applied force.
W=mg=0.1kg×9.8m/s2=0.98N
The maximum static friction force fmaxs can be calculated using the formula:
fmaxs=μsN
where μs=0.5 is the coefficient of friction.
Since the block is in equilibrium vertically, the normal force N is equal to the weight of the block:
N=W=0.98N
fmaxs=μsN=0.5×0.98N=0.49N
The frictional force f will adjust to prevent the block from sliding down. Since the applied force F=5N is greater than the maximum static friction force fmaxs=0.49N, the frictional force will be equal to its maximum value:
f=fmaxs=0.49N
The magnitude of the frictional force acting on the block is 0.49N.
Topper's Solved these Questions
- INTRODUCTION TO VECTORS & FORCES Book:VMC MODULES ENGLISHChapter:INTRODUCTION TO VECTORS & FORCES Exercise:JEE Main ( ARCHIVE ) ( LEVEL-1)
Explore 12 Videos
- GRAVITATIONBook:VMC MODULES ENGLISHChapter:GRAVITATIONExercise:JEE Advance (Archive) TRUE/FALSE
Explore 1 Video
- JEE MAIN - 5Book:VMC MODULES ENGLISHChapter:JEE MAIN - 5Exercise:PART I : PHYSICS (SECTION - 2)
Explore 5 Videos
Similar Questions
A block of mass 0.1 kg is held against a wall applying a horizontal force of 5 N on the block. If the coefficient of friction between the block and the wall is 0.5, the magnitude of the frictional force acting on the block is :
View SolutionA block of mass 1 kg is pressed against a wall by applying a horizontal force of 10N on the block. If the coefficient of friction between the block and the wall is 0.5, magnitude of the frictional force acting on the block is
View Solution
Knowledge Check
A block of mass 1 kg lies on a horizontal surface in a truck. The coefficient of static friction between the block and the surface is 0.6. If the acceleration of the truck is 5m/s2, the frictional force acting on the block is…………newtons.
A10NB5NC2.5ND20NA block of mass M is held against a rough vertical wall by pressing it with a finger . If the coefficient of friction between the block and the wall is μ and the acceleration due to gravity is g , calculate the minimum force required to be applied by the finger to hold the block against the wall.
AμMgBMgCMgμD2μMg
A force of 200N is applied as shown in the figure on block of 3 kg. The coefficient of friction between the block and the wall is 0.3. Find the friction acting on the block. (in N) {Take g = 10 m/s2

View SolutionA block of mass 1 kg lies on a horizontal surface in a truck. The coefficient of static friction between the block and the surface is 0.6. If the acceleration of the truck is 5m/s2, the frictional force acting on the block is…………newtons.
View SolutionA body is pushed against vertical wall as shown. If the coefficient of friction between the body and the wall is 0.5, the magnitude of acceleration of the block is 10 K. Where K is
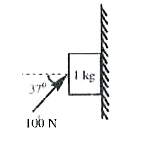
View SolutionGiven in figure are two blocks A and B of weight 20N and 100N, respectively. These are being pressed against a wall by a force F as shown. If the coefficient of friction between the blocks is 0.1 and between block B and the wall is 0.15, the frictional force applied by the wall on block B is:

View SolutionGiven in the figure are two blocks A and B of weight 20 N and 100 N respectively. These are being pressed against a wall by a force F as shown. If the coefficient of friction between the blocks is 0.1 and between block B and the wall is 0.15, the frictional force applied by the wall on block B is
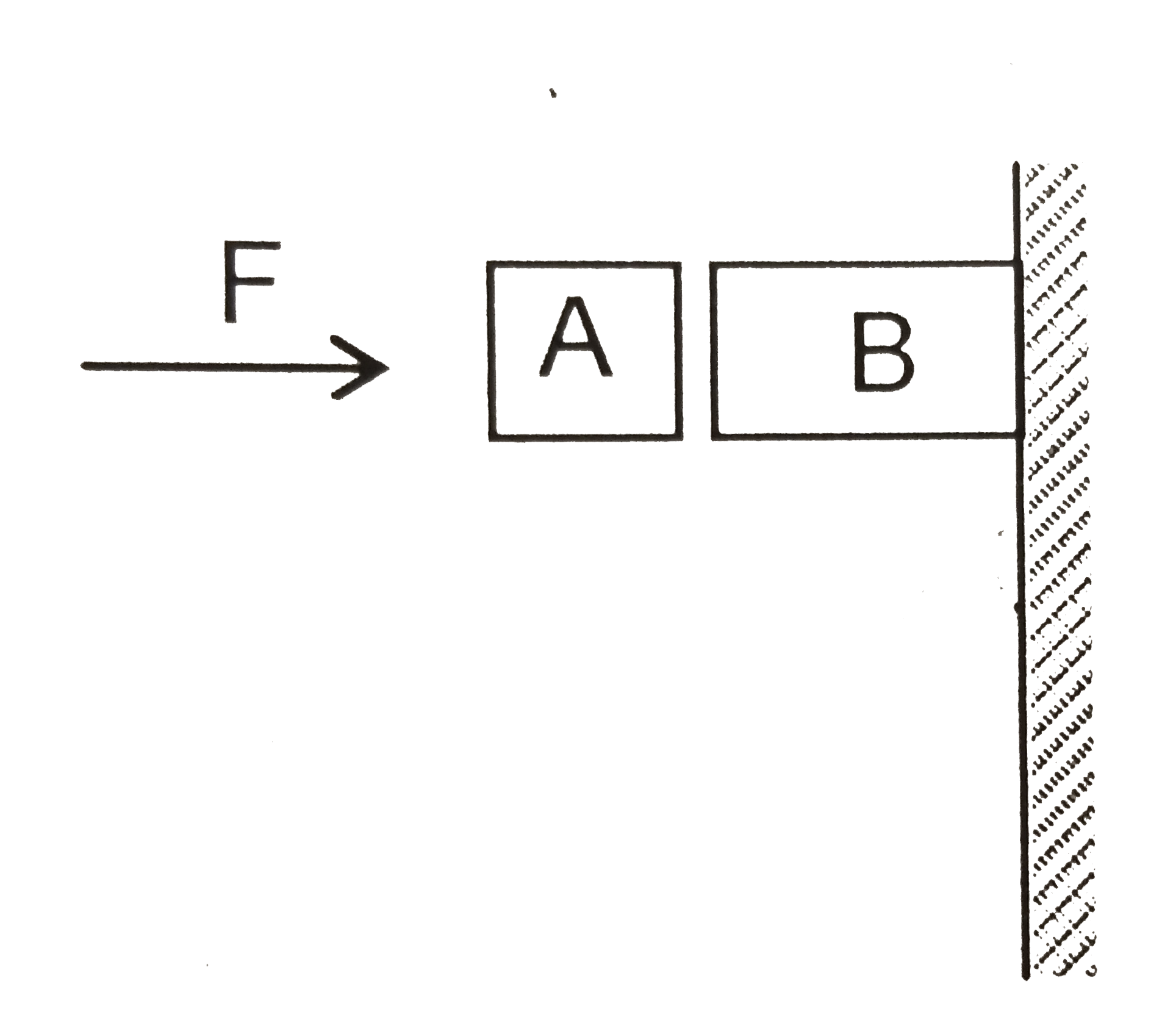
View SolutionA block of mass M is held against a rough vertical wall by pressing it with a finger . If the coefficient of friction between the block and the wall is μ and the acceleration due to gravity is g , calculate the minimum force required to be applied by the finger to hold the block against the wall.
View Solution

