A block of mass M is held against a rough vertical wall by pressing it with a finger . If the coefficient of friction between the block and the wall is μ and the acceleration due to gravity is g , calculate the minimum force required to be applied by the finger to hold the block against the wall.
To solve the problem of finding the minimum force required to hold a block of mass M against a rough vertical wall, we can follow these steps:
Step 1: Identify the Forces Acting on the Block
- The block experiences several forces:
1. The gravitational force acting downward, which is mg (where m is the mass of the block and g is the acceleration due to gravity).
2. The normal force N exerted by the wall on the block, acting horizontally.
3. The force F applied by the finger, acting horizontally against the wall.
4. The frictional force f acting upward, which opposes the downward gravitational force.
Step 2: Set Up the Equilibrium Conditions
- Since the block is in equilibrium, we can set up the following equations based on the forces acting on it:
- In the vertical direction: The upward frictional force must balance the downward gravitational force.
- In the horizontal direction: The normal force must balance the applied force.
Step 3: Write the Equations
1. Vertical Forces:
f=mg
where f is the frictional force.
2. Horizontal Forces:
N=F
where N is the normal force and F is the force applied by the finger.
Step 4: Relate the Frictional Force to the Normal Force
- The maximum frictional force f can be expressed as:
f=μN
where μ is the coefficient of friction.
Step 5: Substitute and Solve for F
- From the vertical forces equation, we have:
μN=mg
- Substituting N=F into this equation gives:
μF=mg
- Rearranging this equation to solve for F:
F=mgμ
Conclusion
- The minimum force required to be applied by the finger to hold the block against the wall is:
F=mgμ
- The block experiences several forces:
1. The gravitational force acting downward, which is mg (where m is the mass of the block and g is the acceleration due to gravity).
2. The normal force N exerted by the wall on the block, acting horizontally.
3. The force F applied by the finger, acting horizontally against the wall.
4. The frictional force f acting upward, which opposes the downward gravitational force.
- Since the block is in equilibrium, we can set up the following equations based on the forces acting on it:
- In the vertical direction: The upward frictional force must balance the downward gravitational force.
- In the horizontal direction: The normal force must balance the applied force.
1. Vertical Forces:
f=mg
where f is the frictional force.
N=F
where N is the normal force and F is the force applied by the finger.
- The maximum frictional force f can be expressed as:
f=μN
where μ is the coefficient of friction.
- From the vertical forces equation, we have:
μN=mg
- Substituting N=F into this equation gives:
μF=mg
- Rearranging this equation to solve for F:
F=mgμ
- The minimum force required to be applied by the finger to hold the block against the wall is:
F=mgμ
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Long answer Type Questions
9 Videos
- LAWS OF MOTIONBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Very short answer type Questions
12 Videos
- KINETIC THEORYBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - KINETIC THEORYEXERCISE - Multiple Choice Questions (MCQs)
31 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - Long Answer Type Questions
3 Videos
Similar Questions
A body is pushed against vertical wall as shown. If the coefficient of friction between the body and the wall is 0.5, the magnitude of acceleration of the block is 10 K. Where K is
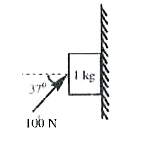
View SolutionA block of mass 0.1 is held against a wall applying a horizontal force of 5N on block. If the coefficient of friction between the block and the wall is 0.5, the magnitude of the frictional force acting on the block is:
View Solution
Knowledge Check
A girl press her physics text book against a rough vertical wall with her hand. The direction of the frictional force on the book exerted by the wall is
AdownwardsBupwardsCout from the wallDinto the wall
A block of mass 1 kg is pushed against a rough vertical wall of μ=0.1
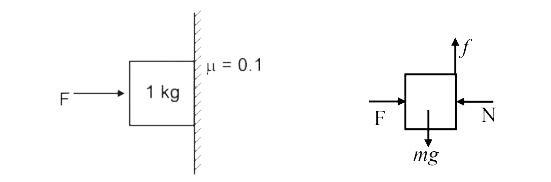
For F = 150, 50 or 100 N the force of friction on the blocks is respectively :
View SolutionA block of mass 1 kg is held at rest against a rough vertical surface by pushing by a force F horizontally. The coefficient of friction is 0.5. When

View SolutionA block of mass 1 kg is pressed against a wall by applying a horizontal force of 10N on the block. If the coefficient of friction between the block and the wall is 0.5, magnitude of the frictional force acting on the block is
View SolutionA block of mass 0.1 kg is held against a wall applying a horizontal force of 5 N on the block. If the coefficient of friction between the block and the wall is 0.5, the magnitude of the frictional force acting on the block is :
View SolutionA block of mass m sides down an inclined right angled trough .If the coefficient of friction between block and the trough is μk acceleration of the block down the plane is

View Solution
A rough vertical board has an acceleration a so that a 2 kg block pressing against it dows not fall. The coefficient of friction between the block and the board should be
View Solution
A rough vertical board has an acceleration a so that a 2 kg block pressing against it dows not fall. The coefficient of friction between the block and the board should be
View Solution
