A rope of length L and uniform linear density is hanging from the ceiling. A transverse wave pulse, generated close to the free end of the rope, travels upwards through the rope. Select the correct option:
The speed of the pulse decreases as it moves up
The time taken by the pulse to travel the length of the rope is proportional to
The tension will be constant along the length of the rope
The speed of the pulse will be constant along the length of the rope
To solve the problem, we need to analyze the behavior of a transverse wave pulse traveling upward through a hanging rope. Let's break down the solution step by step.
Step 1: Understand the System
We have a rope of length L with a uniform linear density μ hanging from the ceiling. A transverse wave pulse is generated near the free end of the rope and travels upwards.
Step 2: Identify the Variables
- Let T be the tension in the rope at a height y from the bottom.
- The mass of the rope segment of length y is given by m=μy.
- The weight of this segment, which contributes to the tension, is mg=μyg.
Step 3: Determine the Tension
The tension T at a height y can be expressed as:
T=μyg
This shows that the tension increases linearly with y.
Step 4: Wave Speed Formula
The speed v of a transverse wave in a rope is given by the formula:
v=√Tμ
Substituting the expression for tension:
v=√μygμ=√yg
This indicates that the speed of the wave pulse depends on the height y from the bottom of the rope.
Step 5: Analyze the Options
1. Speed of the pulse decreases as it moves up: This is incorrect because v increases with y.
2. Time taken by the pulse to travel the length of the rope is proportional to √L: We will verify this.
3. The tension will be constant along the length of the rope: This is incorrect since tension varies with y.
4. The speed of the pulse will be constant along the length of the rope: This is incorrect as speed varies with y.
Step 6: Calculate the Time Taken
To find the time T taken for the pulse to travel the length L, we can set up the following relationship:
dydt=√yg
Rearranging gives:
dt=dy√yg
Integrating from y=0 to y=L:
T=∫L0dy√yg=1√g∫L0y−1/2dy
The integral evaluates to:
∫L0y−1/2dy=2√L
Thus,
T=2√L√g⟹T∝√L
Conclusion
The correct option is that the time taken by the pulse to travel the length of the rope is proportional to √L.
We have a rope of length L with a uniform linear density μ hanging from the ceiling. A transverse wave pulse is generated near the free end of the rope and travels upwards.
- Let T be the tension in the rope at a height y from the bottom.
- The mass of the rope segment of length y is given by m=μy.
- The weight of this segment, which contributes to the tension, is mg=μyg.
The tension T at a height y can be expressed as:
T=μyg
This shows that the tension increases linearly with y.
The speed v of a transverse wave in a rope is given by the formula:
v=√Tμ
Substituting the expression for tension:
v=√μygμ=√yg
This indicates that the speed of the wave pulse depends on the height y from the bottom of the rope.
1. Speed of the pulse decreases as it moves up: This is incorrect because v increases with y.
2. Time taken by the pulse to travel the length of the rope is proportional to √L: We will verify this.
3. The tension will be constant along the length of the rope: This is incorrect since tension varies with y.
4. The speed of the pulse will be constant along the length of the rope: This is incorrect as speed varies with y.
To find the time T taken for the pulse to travel the length L, we can set up the following relationship:
dydt=√yg
Rearranging gives:
dt=dy√yg
Integrating from y=0 to y=L:
T=∫L0dy√yg=1√g∫L0y−1/2dy
The integral evaluates to:
∫L0y−1/2dy=2√L
Thus,
T=2√L√g⟹T∝√L
The correct option is that the time taken by the pulse to travel the length of the rope is proportional to √L.
Topper's Solved these Questions
Similar Questions
A string is hanging from a rigid support. A transverse
pulse is excited at its free end. The speed at which the
pulse travels a distance x is proportional to
View SolutionA uniform rope of elngth l and mass m hangs vertically from a rigid support. A block of mass m is attached to the free end of the rope. A transverse pulse of wavelength λ is produced at the lower end of the rope. The wavelength of the pulse, when it reaches the top of the rope. is aλ. Find a2

View Solution
Knowledge Check
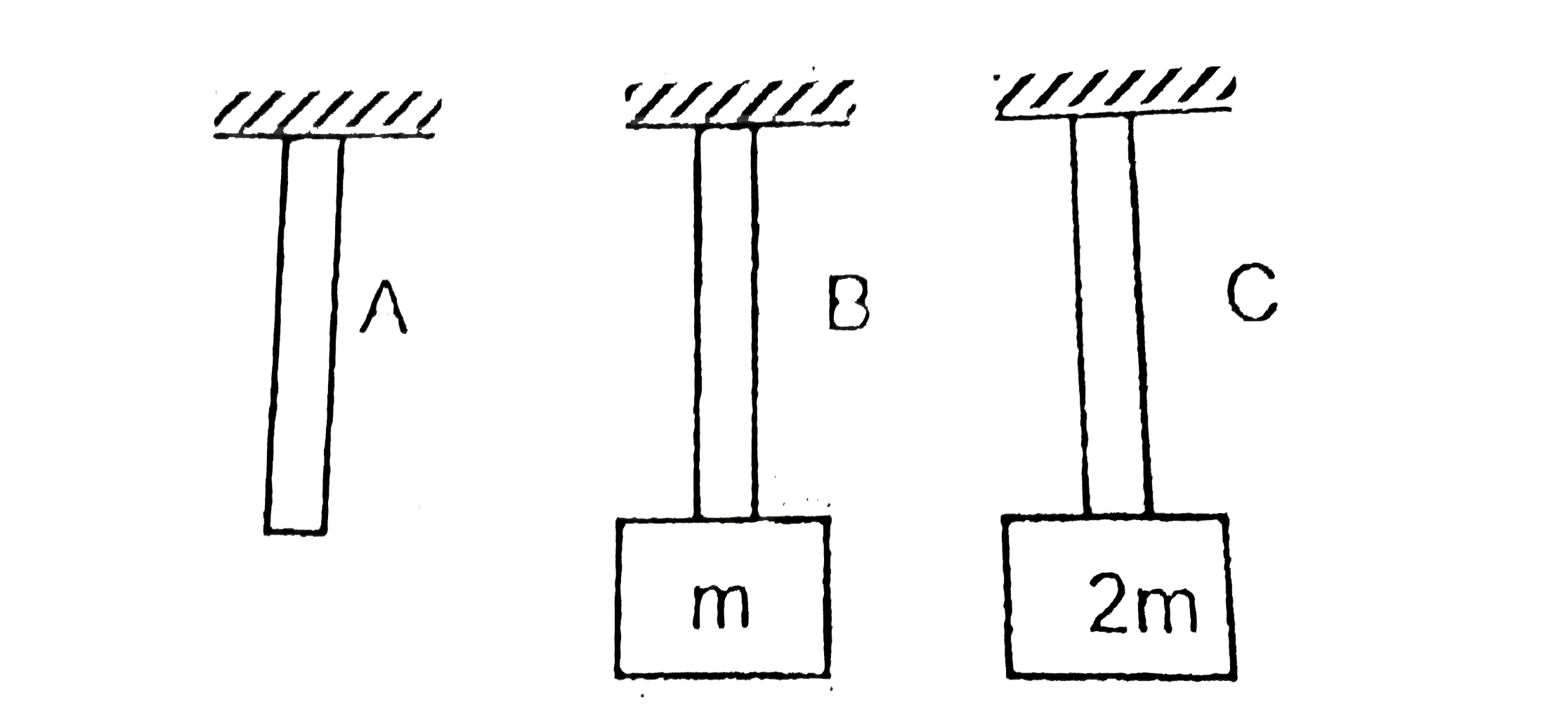
Consider the three ropes of same length and same linear density as (shown in figure) suspended from the ceiling.
A pulse is generated at the lowest point of the three ropes simultaneously. Choose the correct statements(s)ATime taken by pulse to reach the top is same for all three.BAcceleration with which pulses move up is same for A and BCAcceleration with which pulses move up is same for B and CDTime taken by pulse to reach the top is greater for B than C.A rope of length L and mass m hangs freely from the ceiling. The velocity of transverse wave as a function of position x-along the rope is proportional to
Ax0B√xC1√xDxA rope of length L and mass m hangs freely from the ceiling. The velocity of transverse wave as a function of position x from the bottom is proportional to
Ax0B√xC1√xDx
A uniform rope of length 12m and mass 6kg hangs vertically from a rigid support. A block of mass 2kg is attached to the free end of the rope. A transverse pulse of wavelength 0.06m is produced at the lower end of the rope. What is the wavelength of the pulse whwn it reaches the top of the rope?
View SolutionA rope of length L and mass m hangs freely from the ceiling. The velocity of transverse wave as a function of position x from the bottom is proportional to
View SolutionA string is hanging from a rigid support. A transverse pulse is excited at its free end. The speed at which the pulse travels a distance x is proportional to
View SolutionA uniform rope having linear density λ hangs vertically from the ceiling and its lower end is free. A disturbance produced at the free end has a speed v0 at point P midway on the rope . Then the time taken by the disturbance pulse to reach the ceiling is
View SolutionA uniform rope of legnth L and mass m1 hangs vertically from a rigid support. A block of mass m2 is attached to the free end of the rope. A transverse pulse of wavelength λ1 is produced at the lower end of the rope. The wavelength of the pulse when it reaches the top of the rope is λ2. The ratio λ2λ1 is
View Solution