A uniform rope having linear density λ hangs vertically from the ceiling and its lower end is free. A disturbance produced at the free end has a speed v0 at point P midway on the rope . Then the time taken by the disturbance pulse to reach the ceiling is
4μ0g
2√2V0g
2√2V20λg
2√2V0λg
The correct Answer is:B
To solve the problem of finding the time taken by a disturbance pulse to reach the ceiling of a vertically hanging rope, we can follow these steps:
1. Understanding the Setup:
- We have a uniform rope hanging vertically from the ceiling with linear density λ.
- The lower end of the rope is free, and a disturbance is produced at this end.
- We need to determine the time it takes for this disturbance to travel to the ceiling.
2. Identifying the Variables:
- Let the length of the rope be L.
- The linear density of the rope is given as λ.
- The speed of the disturbance at point P (midway) is v0.
3. Finding the Tension in the Rope:
- At a distance x from the ceiling, the tension T in the rope due to the weight of the rope below that point is:
T=λgx
- Here, g is the acceleration due to gravity.
4. Calculating the Velocity of the Wave:
- The speed of a transverse wave on a rope is given by:
v=√Tμ
- Where μ is the linear mass density, which is λ in this case.
- Substituting for T:
v=√λgxλ=√gx
5. Using the Given Condition:
- At point P (midway), where x=L2, the speed of the wave is given as v0:
v0=√gL2
- Squaring both sides gives:
v20=gL2
- Rearranging gives:
L=2v20g
6. Setting Up the Time Calculation:
- The relationship between distance dx, time dt, and velocity v is:
v=dxdt
- Substituting v=√gx:
√gx=dxdt⇒dt=dx√gx
7. Integrating to Find Total Time:
- To find the total time t taken for the disturbance to travel from x=0 to x=L:
t=∫L0dx√gx
- This can be simplified:
t=1√g∫L0x−1/2dx=1√g(2√x)L0=2√L√g
8. Substituting for L:
- From our earlier result, we substitute L=2v20g:
t=2√2v20g√g=2⋅√2⋅v0g
9. Final Result:
- Thus, the time taken by the disturbance pulse to reach the ceiling is:
t=2√2v0g
- We have a uniform rope hanging vertically from the ceiling with linear density λ.
- The lower end of the rope is free, and a disturbance is produced at this end.
- We need to determine the time it takes for this disturbance to travel to the ceiling.
- Let the length of the rope be L.
- The linear density of the rope is given as λ.
- The speed of the disturbance at point P (midway) is v0.
- At a distance x from the ceiling, the tension T in the rope due to the weight of the rope below that point is:
T=λgx
- Here, g is the acceleration due to gravity.
- The speed of a transverse wave on a rope is given by:
v=√Tμ
- Where μ is the linear mass density, which is λ in this case.
- Substituting for T:
v=√λgxλ=√gx
- At point P (midway), where x=L2, the speed of the wave is given as v0:
v0=√gL2
- Squaring both sides gives:
v20=gL2
- Rearranging gives:
L=2v20g
- The relationship between distance dx, time dt, and velocity v is:
v=dxdt
- Substituting v=√gx:
√gx=dxdt⇒dt=dx√gx
- To find the total time t taken for the disturbance to travel from x=0 to x=L:
t=∫L0dx√gx
- This can be simplified:
t=1√g∫L0x−1/2dx=1√g(2√x)L0=2√L√g
- From our earlier result, we substitute L=2v20g:
t=2√2v20g√g=2⋅√2⋅v0g
- Thus, the time taken by the disturbance pulse to reach the ceiling is:
t=2√2v0g
Topper's Solved these Questions
- PHYSICS PART-IIIBook:FIITJEEChapter:PHYSICS PART-IIIExercise:MCQ (MULTIPLE CORRECT)
Explore 18 Videos
- PHYSICS PART-IIIBook:FIITJEEChapter:PHYSICS PART-IIIExercise:ASSERTION -REASONING MCQ (SINGLE CORRECT)
Explore 12 Videos
- PHYSICS PART-IIIBook:FIITJEEChapter:PHYSICS PART-IIIExercise:ASSIGNMENT SECTION-II SUBJECTIVE
Explore 27 Videos
- OPTICSBook:FIITJEEChapter:OPTICSExercise:NUMERICAL BASED QUESTIONS
Explore 2 Videos
- PHYSICS PART2Book:FIITJEEChapter:PHYSICS PART2Exercise:Numerical Based Question Decimal Type
Explore 6 Videos
Similar Questions
A rope of length L and uniform linear density is hanging from the ceiling. A transverse wave pulse, generated close to the free end of the rope, travels upwards through the rope. Select the correct option:
View SolutionA uniform rope of mass m per unit length, hangs vertically from a support so that the lower end just touches the table top shown in figure. If it is released, show that at the time a length y of the rope has fallen, the force on the table is equivalent to the weight of the length 3y of the rope.

View Solution
Knowledge Check
A heavy unifrm rope hangs vertically from the ceiling, with its lower end free. A disturbance on the rope travelling upward from the lower end has a velocyt v at a distance x from the lower end.
Av∝1/xBv∝xCv∝√xDv∝1/√xA uniform rope having some mass hinges vertically from a rigid support. A transverse wave pulse is produced at the lower end. The speed (v) of the wave pulse varies with height (h) from the lower end as :-
A B
B C
C D
D
A Uniform rope having mass m hags vertically from a rigid support. A transverse wave pulse is produced at the lower end. The speed v of wave pulse varies with height h from the lower end as
A B
B C
C D
D
A uniform rope of elngth l and mass m hangs vertically from a rigid support. A block of mass m is attached to the free end of the rope. A transverse pulse of wavelength λ is produced at the lower end of the rope. The wavelength of the pulse, when it reaches the top of the rope. is aλ. Find a2

View SolutionA uniform rope of mass 0.1kg and length 2.45m hangs from a ceiling.
(a) Find the speed of transverse wave in the rope at a point 0.5m distant from the lower end.
(b) Calculate the time taken by a transverse wave to travel the full length of the rope.

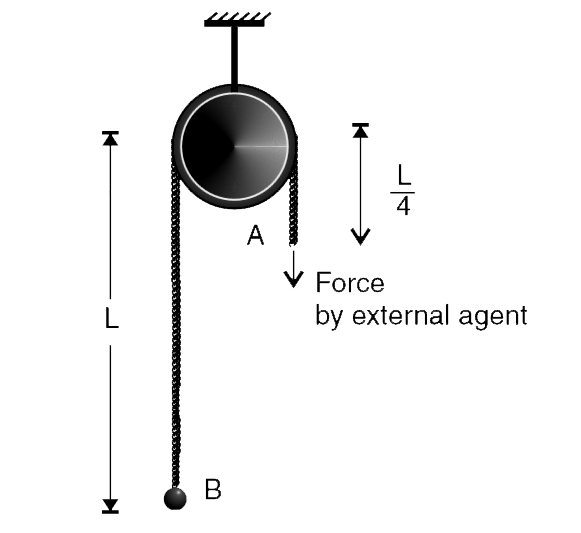
View SolutionA uniform rope of linear mass density λ (kg/m) passes over a smooth pulley of negligible dimension. At one end B of the rope there is a small particle having mass one fifty of the rope. Initially the system is held at rest with length L of the rope on one side and length L4 on the other side of the pulley (see fig). The external agent begins to pull the end A downward. Find the minimum work that the agent must perform so that the small particle will definitely reach the pulley.
View SolutionA uniform rope having some mass hinges vertically from a rigied support. A transverse wave pulse is produced at the lower end. The speed (v) of the wave pulse varies with height (h) from the lower end as :-
View SolutionA uniform rope of length 20m and mass 5kg is hanging vertically from a rigid support. A block of mass 4kg is attached to the free end. The wave length of the transverse wave pulse at the lower end of the rope is 0.04 m. The wavelength of the same pulse as it reaches the top is
View Solution