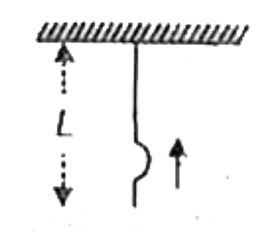
A rope has it mass per unit length λ given by the relation λ=[φe/(1+xL)2]
where λ0 is a constant where L being the length of the rope. The highest point is fixed to the ceilling A transverse pulse is given at the bottom of the rope . find the time taken by the pulse to reach to the highest point
![A rope has it mass per unit length lambda given by the relation lambda=[varphie//(1+x/L)^2] where lambda0 is a constant where L being the length of the rope. The highest point is fixed to the ceilling A transverse pulse is given at the bottom of the rope . find the time taken by the pulse to reach to the highest point](https://d10lpgp6xz60nq.cloudfront.net/physics_images/RNK_SM_FIITJEE_PHY_P3_E02_001_Q01.png)
2√Lgin(1+√2)
Topper's Solved these Questions
- PHYSICS PART-IIIBook:FIITJEEChapter:PHYSICS PART-IIIExercise:ASSIGNMENT SECTION-II MCQ (SINGLE CORRECT)
Explore 47 Videos
- PHYSICS PART-IIIBook:FIITJEEChapter:PHYSICS PART-IIIExercise:MCQ (MULTIPLE CORRECT)
Explore 18 Videos
- PHYSICS PART-IIIBook:FIITJEEChapter:PHYSICS PART-IIIExercise:NUMERICAL BASED QUESTIONS DECIMAL TYPE
Explore 11 Videos
- OPTICSBook:FIITJEEChapter:OPTICSExercise:NUMERICAL BASED QUESTIONS
Explore 2 Videos
- PHYSICS PART2Book:FIITJEEChapter:PHYSICS PART2Exercise:Numerical Based Question Decimal Type
Explore 6 Videos
Similar Questions
A uniform rope having linear density λ hangs vertically from the ceiling and its lower end is free. A disturbance produced at the free end has a speed v0 at point P midway on the rope . Then the time taken by the disturbance pulse to reach the ceiling is
View SolutionA pulse is generated at lower end to a hanging rope of uniform density and length L. The speed of the pulse when it reaches the mid point of rope is
View Solution
Knowledge Check
A block of mass 2m is hanging at the lower and of a ropeof mass m and length the l, the other end being fixed to the ceililng. A pulse of wavelength λ0 is produced at the lower of the rope.
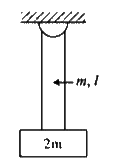
The time taken by the pulse to reach the other end of the rope is:A2√lg(√3−1)B2√lg(√3−2)C2√lgD2√lg(√3−√2)A rope of length L has its mass per unit langth λ varies according to the function λ(x)=ex/L. The rope is pulled by a constant force of 1 N on a smooth horizontal surface. The tension in the rope at x=L/2 is :
 A0.50 NB0.38 NC0.62 NDNone
A0.50 NB0.38 NC0.62 NDNoneThe mass per unit length of a non - uniform rod of length L is given μ=λx2 , where λ is a constant and x is distance from one end of the rod. The distance of the center of mas of rod from this end is
AL2BL4C3L4DL3
A block of mass 2m is hanging at the lower and of a ropeof mass m and length the l, the other end being fixed to the ceililng. A pulse of wavelength λ0 is produced at the lower of the rope.
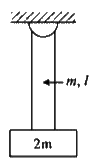
The speed of the pulseat the mid point of rope is:
View SolutionA block of mass 2m is hanging at the lower and of a ropeof mass m and length the l, the other end being fixed to the ceililng. A pulse of wavelength λ0 is produced at the lower of the rope.
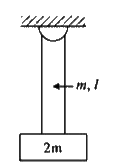
The wavelength of the pulse when it reaches the other end of the rope is :
View SolutionA rope of length L and mass m hangs freely from the ceiling. The velocity of transverse wave as a function of position x from the bottom is proportional to
View SolutionA uniform rope having linear density λ hangs vertically from the ceiling and its lower end is free. A disturbance produced at the free end has a speed v0 at point P midway on the rope . Then the time taken by the disturbance pulse to reach the ceiling is
View SolutionIf a transverse pulse is created at the topmost point of a uniform rope suspended vertically, then
View Solution

