A circuit consisits of a coil with inductance L and an uncharged capacitor of capacitance C. The coil is in a constant uniform magnetic field such that the flux through the coil is Φ. At time t=0, the magnetic filed is abruptly switched off Let ω0=1/√LC and ignore the resistance of the circuit. Then,
current m the circuit is I(t)=(Φ/l)cosω0t
magnitude of the charge on the capacitor is |Q(t)|=2Cω0|sinω0t|
initial current m the circuit is infinite
initial charge on the capacitor is Cω0Φ
To solve the problem step by step, we will analyze the behavior of the LC circuit when the magnetic field is abruptly switched off.
Step 1: Understanding the Initial Conditions
At time t=0, the magnetic field is abruptly switched off. The coil has an inductance L and the capacitor has a capacitance C. The initial magnetic flux through the coil is given as Φ.
Hint: Remember that the initial conditions are crucial for determining the behavior of the circuit after the switch-off.
Step 2: Determine the Initial Current
When the magnetic field is switched off, an electromotive force (EMF) is induced in the circuit due to the change in magnetic flux. According to Faraday's law of electromagnetic induction, the induced EMF E is given by:
E=−dΦdt
At t=0, since the magnetic field is switched off, the rate of change of flux is maximum, leading to an initial current I0. The maximum EMF can be expressed as:
Emax=Φ⋅ω0
where ω0=1√LC.
Hint: The induced EMF is related to the rate of change of magnetic flux, and it can be calculated using the initial flux and angular frequency.
Step 3: Calculate the Maximum Current
The maximum current I0 in the circuit can be found using the relationship between EMF, inductance, and current:
I0=EmaxXL
where XL=ω0L is the inductive reactance. Substituting the expression for EMF:
I0=Φ⋅ω0ω0L=ΦL
Hint: The maximum current is directly proportional to the initial magnetic flux and inversely proportional to the inductance.
Step 4: Determine the Current as a Function of Time
The current I(t) in the LC circuit can be expressed as a function of time t:
I(t)=I0cos(ω0t)
Substituting I0:
I(t)=ΦLcos(ω0t)
Hint: The oscillatory nature of the LC circuit leads to a cosine function for current, reflecting the energy exchange between the inductor and capacitor.
Step 5: Calculate the Charge on the Capacitor
The charge Q(t) on the capacitor can be related to the current by:
Q(t)=C⋅V(t)
where V(t) is the voltage across the capacitor. The voltage can be expressed as:
V(t)=Q(t)C
Using the relationship between current and charge:
I(t)=dQdt
Integrating the current with respect to time gives:
Q(t)=CΦsin(ω0t)
Hint: The charge on the capacitor oscillates as a sine function, reflecting the energy transfer in the LC circuit.
Summary of Results
- The initial current in the circuit is I0=ΦL.
- The current as a function of time is I(t)=ΦLcos(ω0t).
- The charge on the capacitor as a function of time is Q(t)=CΦsin(ω0t).
At time t=0, the magnetic field is abruptly switched off. The coil has an inductance L and the capacitor has a capacitance C. The initial magnetic flux through the coil is given as Φ.
When the magnetic field is switched off, an electromotive force (EMF) is induced in the circuit due to the change in magnetic flux. According to Faraday's law of electromagnetic induction, the induced EMF E is given by:
The maximum current I0 in the circuit can be found using the relationship between EMF, inductance, and current:
The current I(t) in the LC circuit can be expressed as a function of time t:
The charge Q(t) on the capacitor can be related to the current by:
- The initial current in the circuit is I0=ΦL.
- The current as a function of time is I(t)=ΦLcos(ω0t).
- The charge on the capacitor as a function of time is Q(t)=CΦsin(ω0t).
Topper's Solved these Questions
Similar Questions
An oscillating circuit consists of an inductance coil L and a capacitor with capacitance C. The resistance of the coil and the lead wires is negligible . The coil is placed in a permanent magnetic filed so that the total flux passing through all the turns of the coild is equal to Φ . At the moment t=0 the magnetic field was switched off. Assuiming the switching off time to be negligible compared to the natural oscillation paeriod of the cirucuit, find the circuit current as a fuction of time t
View SolutionIf plane of coil and uniform magnetic field B(4T0 is same then torque on the current carrying coil is

View Solution
Knowledge Check
A coil with resistance R is placed in a magnetic field. The flux linked with the coil is ϕ. If the magnetic filed suddently reverses in direction, how much charge will circulate in the coil?
Aϕ2RBϕRC2ϕRDzeroA closed coil with a resistance 2R is placed in a magnetic field. The flux linked with the coil is phi .if the magnetic field is suddenly reversed in direction , the charge that flows through the coil will be
Aϕ/2RBπ/RC2ϕ/RDzeroThe graph shows the variation in magnetic flux ϕ(t) with time through a coil. Which of the statements given below is not correct?
 AThere is a change in the direction as well as magnitude of the induced emf between B and DBThe magnitude of the induced emf is maximum between B and CCThere is a change in the direction as well as magnitude of induced emf between A and CDThe induced emf is zero at B
AThere is a change in the direction as well as magnitude of the induced emf between B and DBThe magnitude of the induced emf is maximum between B and CCThere is a change in the direction as well as magnitude of induced emf between A and CDThe induced emf is zero at B
A coil of inductance 0.4 mH is connected to a capacitor of capacitance 400 pF. To what wavelength is this circuit truned ?
View SolutionA circular coil of wire consists of exactly 100 turns with a total resistance 0.20Ω. The area of the coil is 100cm2. The coil is kept in a uniform magnetic field B as shown in Fig. 3.212. The magnetic field is increased at a constant rate of 2Ts−1. Find the induced current in the coil in A.

View SolutionA coil of inductance 1.0H and resistance 100Ω is connected to a battery of emf 12V. Find the energy stored in the magnetic field associated with the coil at an instant 10ms after the circuit is switched on.
View SolutionFind the induced current through a coil at t = 2 s if the magnetic flux through a coil is ϕ=6t3+12t2+5 and the resistance of the coil is 5Ω.
View SolutionThe graph shows the variation in magnetic flux ϕ(t) with time through a coil. Which of the statements given below in not correct?
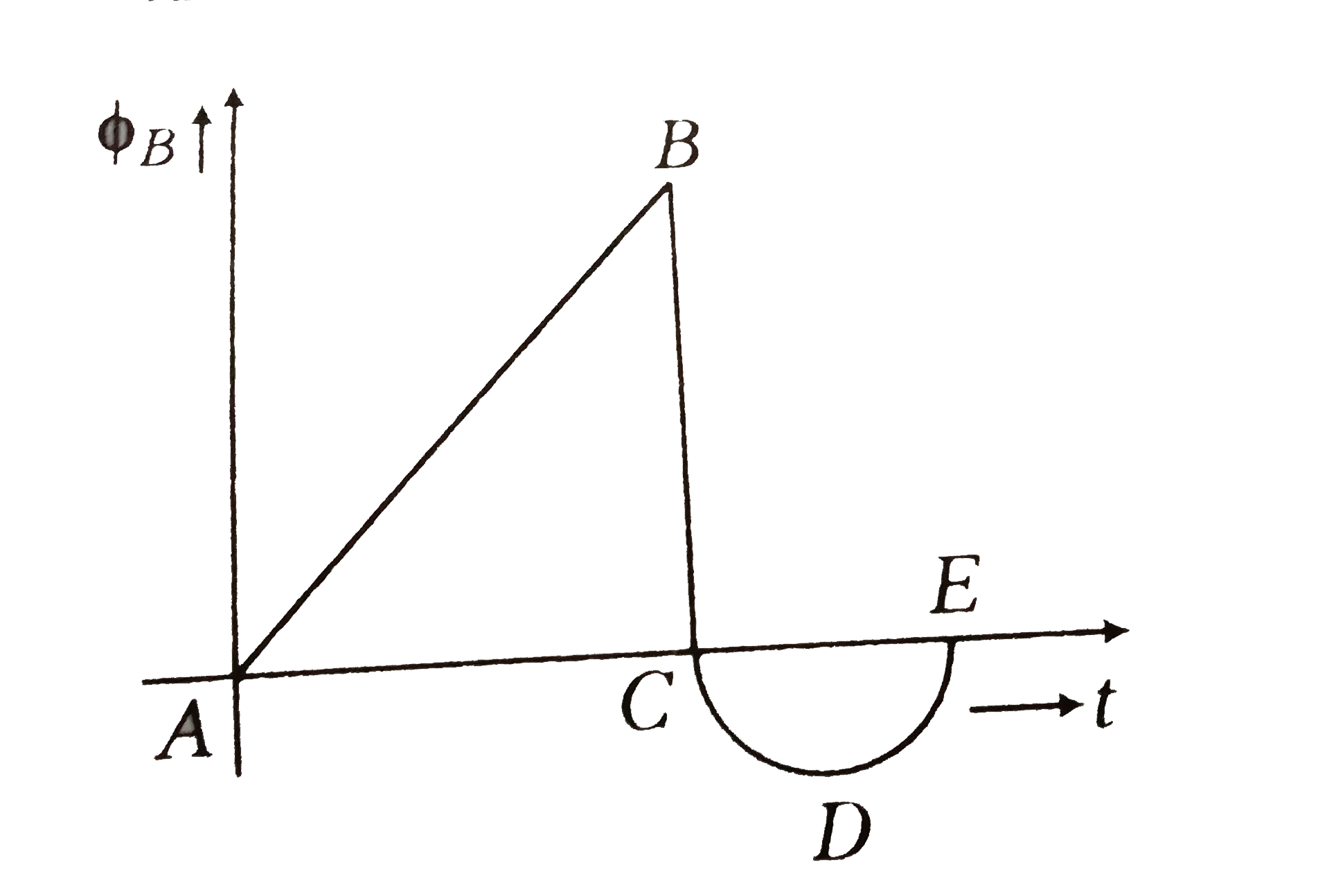
View Solution
