Question

How will the voltage (V) between the two plates of a parallel plate capacitor depend on the distance (d) between the plates, if the charge on the capacitor remains the same?

Options

A.

B.

C.

D.

Explanation

To determine how the voltage (V) between the two plates of a parallel plate capacitor depends on the distance (d) between the plates when the charge (Q) remains constant, we can follow these steps:

1. Understand the Capacitance Formula:
The capacitance (C) of a parallel plate capacitor is given by the formula:
\( C = \frac{A \epsilon_0}{d} \)
where:
- \(C\) is the capacitance,
- \(A\) is the area of the plates,
- \(\epsilon_0\) is the permittivity of free space,
- \(d\) is the distance between the plates.

2. Relationship Between Charge, Capacitance, and Voltage:
The relationship between charge (Q), capacitance (C), and voltage (V) is given by:
\( Q = C \cdot V \)
Rearranging this gives:
\( V = \frac{Q}{C} \)

3. Substituting the Capacitance Formula:
Substitute the expression for capacitance into the voltage equation:
\( V = \frac{Q}{\frac{A \epsilon_0}{d}} = \frac{Q \cdot d}{A \epsilon_0} \)

4. Analyzing the Relationship:
From the equation \(V = \frac{Q \cdot d}{A \epsilon_0}\), we can see that:
- Voltage \(V\) is directly proportional to the distance \(d\) between the plates when the charge \(Q\) is held constant.
- This means that if the distance \(d\) increases, the voltage \(V\) will also increase, assuming \(Q\), \(A\), and \(\epsilon_0\) remain constant.

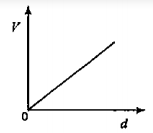
5. Graphical Representation:
If we were to plot a graph of \(V\) versus \(d\):
- The graph would be a straight line with a slope of \(\frac{Q}{A \epsilon_0}\), indicating a linear relationship.
- The line would not pass through the origin because when \(d = 0\), \(V\) would theoretically be undefined.

Conclusion:
Thus, the voltage \(V\) between the two plates of a parallel plate capacitor is directly proportional to the distance \(d\) between the plates when the charge \(Q\) remains constant.