Question

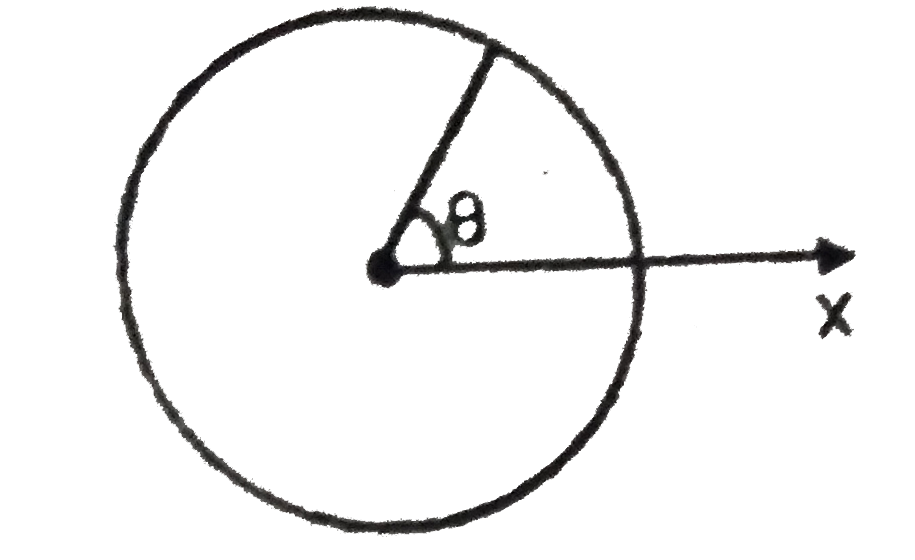
A charge +q is distributed over a thin ring of radius r with line charge density ${\displaystyle \lambda =q{\sin }^2\theta /\left(\pi r\right)}$. Note that the ring is in the x-y plane and ${\displaystyle \theta }$ is the angle made by ${\displaystyle \overrightarrow{r}}$ with the x axis. The work done by the electric force in displacing a point charge +Q from the center of the ring to infinity is

Options

A. equal to `qQ//2piepsilon_0r`
B. equal to `qQ//4piepsilon_0r`
C. equal to zero only if the path is a straight line perpendicular to the plane of the ring
D. equal to `qQ//8piepsilon_0r`

Explanation

To solve the problem of finding the work done by the electric force in displacing a point charge +Q from the center of a charged ring to infinity, we can follow these steps:

Step 1: Understand the Setup
We have a thin ring of radius \( r \) in the xy-plane with a total charge \( +q \) distributed over it. The line charge density \( \lambda \) is given by:
\( \lambda = \frac{q \sin^2 \theta}{\pi r} \)
where \( \theta \) is the angle made by the radius vector with the x-axis.

Step 2: Calculate the Electric Potential at the Center of the Ring
The electric potential \( V \) at a point due to a charge distribution is given by:
\( V = k \int \frac{dq}{r} \)
where \( k = \frac{1}{4 \pi \epsilon_0} \) is Coulomb's constant, and \( dq \) is the infinitesimal charge element.

Since the potential is a scalar quantity, we can consider the total charge \( q \) at the center of the ring. The potential at the center of the ring (where the point charge +Q is initially located) can be calculated as:
\( V_{\text{center}} = k \frac{q}{r} \)

Step 3: Calculate the Potential Energy at the Center
The potential energy \( U \) of the point charge +Q at the center of the ring is given by:
\( U_{\text{center}} = Q \cdot V_{\text{center}} = Q \cdot \left( k \frac{q}{r} \right) = \frac{Qq}{4 \pi \epsilon_0 r} \)

Step 4: Calculate the Potential Energy at Infinity
At infinity, the electric potential is zero, so the potential energy \( U_{\text{infinity}} \) of the charge +Q is:
\( U_{\text{infinity}} = 0 \)

Step 5: Calculate the Work Done
The work done \( W \) by the electric force in moving the charge from the center of the ring to infinity is equal to the change in potential energy:
\( W = U_{\text{infinity}} - U_{\text{center}} = 0 - \frac{Qq}{4 \pi \epsilon_0 r} = -\frac{Qq}{4 \pi \epsilon_0 r} \)

Conclusion
Thus, the work done by the electric force in displacing the point charge +Q from the center of the ring to infinity is:
\( W = -\frac{Qq}{4 \pi \epsilon_0 r} \)