A heater supplying constant power P watts is switched on at time t=0 minutes to raise the temperature of a liquid kept in a calorimeter of negligible heat capacity. A student records the temperature of the liquid T(t) at equal time intervals. A graph is plotted with T(t) on the y-axis versus t on the x-axis. Assume that there is no heat loss to the surroundings during heating. Then,
the graph is a straight line parallel to the time axis
the heat capacity of the liquid is inversely proportional to the slope of the graph.
If some heat were lost at a constant rate to the surroundings during heating, the graph would be a straight line but with a larger slope
the internal energy of the liquid increases quadratically with time.
To solve the problem, we need to analyze the situation where a heater supplies constant power P watts to a liquid in a calorimeter with negligible heat capacity. We will derive the relationship between temperature T(t) and time t and understand the implications of the graph plotted.
1. Understanding Power and Heat Transfer:
The power P supplied by the heater is the rate at which heat is added to the liquid. According to the definition of power:
P=dQdt
where dQ is the heat added in a small time interval dt.
2. Relating Heat to Temperature Change:
The heat added to the liquid can also be expressed using the specific heat capacity C and the mass M of the liquid:
dQ=M⋅C⋅dT
where dT is the change in temperature.
3. Setting Up the Equation:
By equating the two expressions for heat transfer, we have:
P=dQdt=M⋅C⋅dTdt
Rearranging gives:
dT=PM⋅C⋅dt
4. Integrating the Equation:
To find the relationship between temperature and time, we integrate both sides. Assuming the initial temperature at t=0 is T0:
∫TT0dT=PM⋅C∫t0dt
This leads to:
T−T0=PM⋅C⋅t
Rearranging gives:
T(t)=T0+PM⋅C⋅t
5. Graphical Interpretation:
The equation T(t)=T0+PM⋅C⋅t represents a straight line with:
- Y-intercept: T0
- Slope: PM⋅C
6. Conclusion:
The graph of T(t) versus t is a straight line with a slope that is directly proportional to the power P and inversely proportional to the product of mass M and specific heat capacity C.
The power P supplied by the heater is the rate at which heat is added to the liquid. According to the definition of power:
P=dQdt
where dQ is the heat added in a small time interval dt.
The heat added to the liquid can also be expressed using the specific heat capacity C and the mass M of the liquid:
dQ=M⋅C⋅dT
where dT is the change in temperature.
By equating the two expressions for heat transfer, we have:
P=dQdt=M⋅C⋅dTdt
Rearranging gives:
dT=PM⋅C⋅dt
To find the relationship between temperature and time, we integrate both sides. Assuming the initial temperature at t=0 is T0:
∫TT0dT=PM⋅C∫t0dt
This leads to:
T−T0=PM⋅C⋅t
Rearranging gives:
T(t)=T0+PM⋅C⋅t
The equation T(t)=T0+PM⋅C⋅t represents a straight line with:
- Y-intercept: T0
- Slope: PM⋅C
The graph of T(t) versus t is a straight line with a slope that is directly proportional to the power P and inversely proportional to the product of mass M and specific heat capacity C.
Topper's Solved these Questions
Similar Questions
What is the most likely value for CT (molar heat capacity at constant temperature) ?
View SolutionEqual masses of two liquids A and B contained in vessels of negligible heat capacity are supplied heat at the same rate. The temperature-time graphs for the liquids are shown in the figure. If S represents specific heat and L represents latent heat of liquid, then

View Solution
Knowledge Check
A liquid of mass m and specific heat c is heated to a temperature 2T. Another liquid of mass m/2 and specific heat 2 c is heated to a temperature T. If these two liquids are mixed, the resulting temperature of the mixture is
A(2/3)TB(8/5)TC(3/5)TD(3/2)TIf a piece of metal is heated to temperature θ and the allowed to cool in a room which is at temperature θ0, the graph between the temperature T of the metal and time t will be closet to
A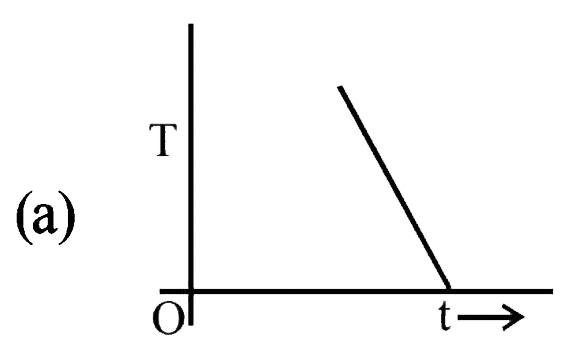 B
B C
C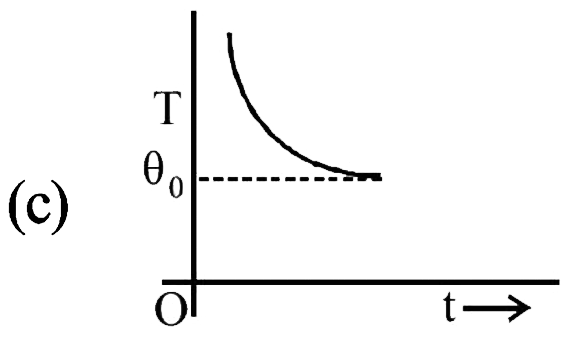 D
D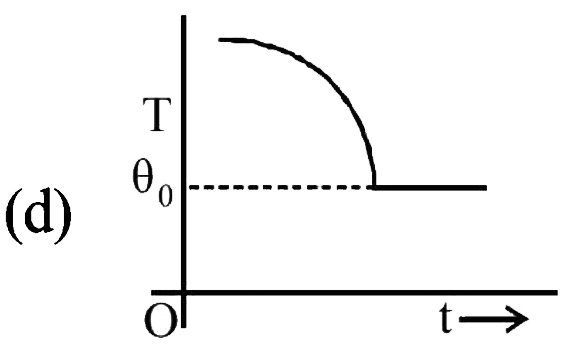
The amount of heat required to raise the temperature of 10 g liquid from 0∘C to 10∘C, if its specific heat (in calg∘C) varies with temperature as 0.3t2 (where t is temperature in ∘C) is
A2 kcalB3 kcalC2.5 kcalD1 kcal
When a certain amount of heat is supplied to a diatomic gas at constant volume, rise in temperature is T0. When same heat is supplied to the gas at constant pressure, find the rise in temperature
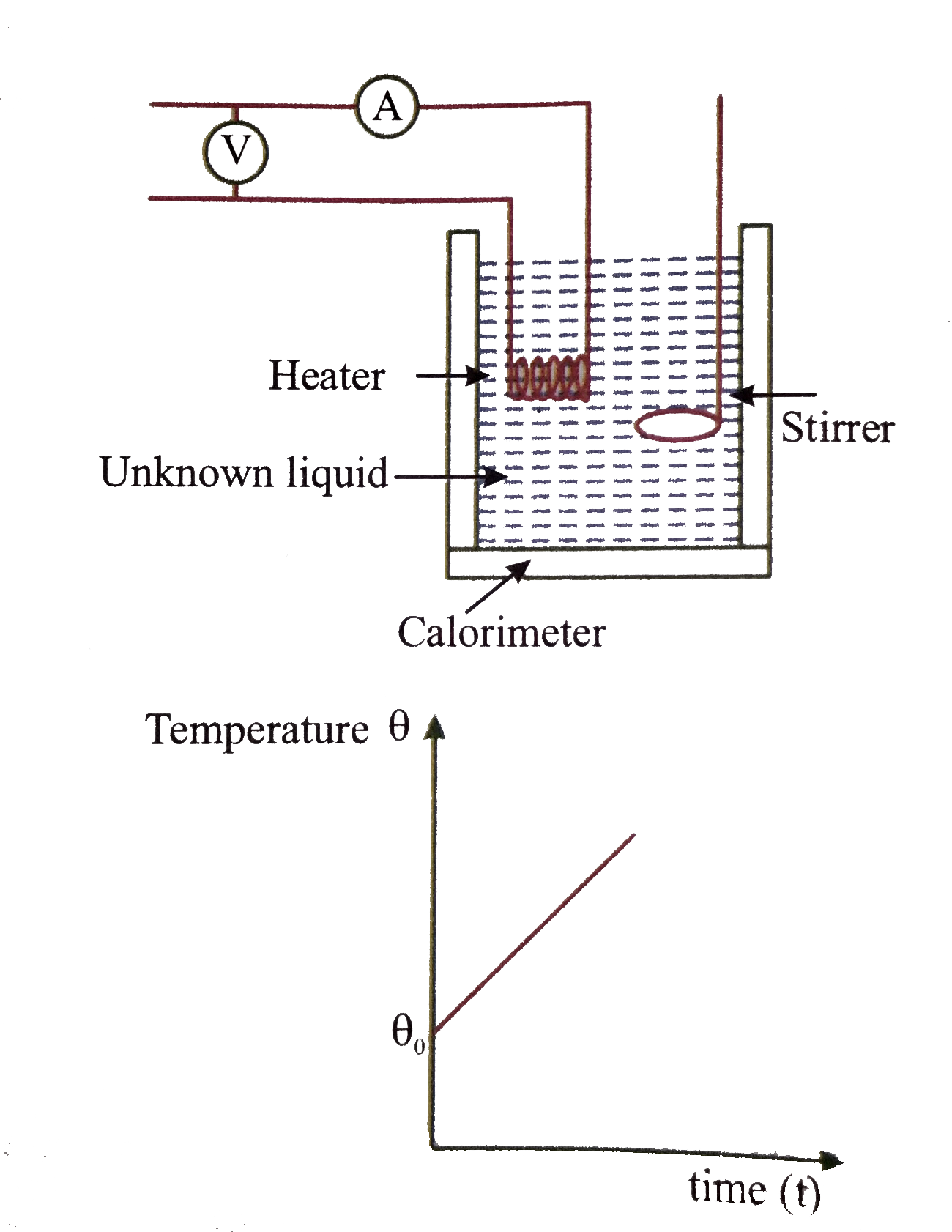
View SolutionFigure shows an electrical calorimeter to determine specific heat capacity of an unknown liquid, First of all, the mass of empty calorimeter (a copper container) is measured and suppose it is m1. Then the unknown liquid is poured in it. Now the combined mass of calorimeter+liquid system is measured and let it be m2. So the mass of liquid is (m2−m1). Initially both were at room temperature (θ0).
Now a heater is immeresed in if for time interval t. The voltage drop across the heater is V and current passing through it is I. Due to heat supplied, the temperature of both the liquid and calorimeter will rise simultaneously. After tsec, heater was switched off, and final temperature is θr. If there is no heat loss to surroundings. Heat supplied by the heater=Heat absorbed by the liquid+heat absorbed by the calorimeter (VI)t=(m2−m1)S1(θf−θ0)+m1Sc(θf−θ0)
The specific heat of the liquid S1=(VI)tθf−θ0−m1Sc(m2−m1)
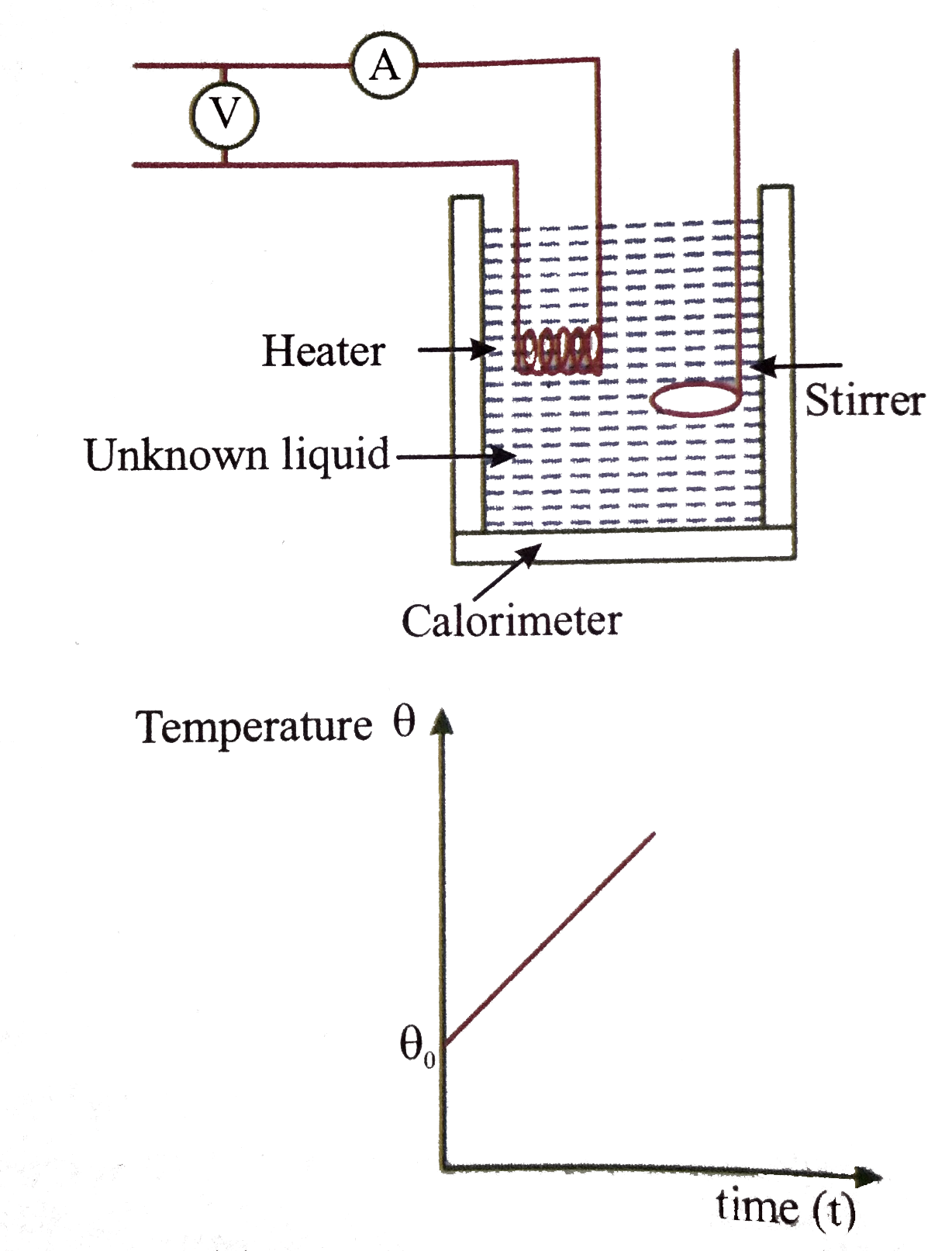
Radiation correction: There can be heat loss to environment. To compensate this loss, a correction is introduced.
Let the heater was on for tsec, and then it is switched off. Now the temperature of the mixture falls due to heat loss to environment. The temperature of the mixture is measured t/2sec. after switching off. Let the fall in temperature during this time is ɛ
Now the corrected final temperature is taken as θf=θf+ɛ
In this experiment voltage across the heater is 100.0V and current is 10.0A, and heater was switched on for t=700.0sec. Initially all elements were at room temperature θ∘=10.0∘C and final temperature was measured as θf=73.0∘C.
Mass of empty calorimeter ws 1.0kg and the combined mass of calorimeter + liquid is 3.0kg. The specific heat capacity of the calorimeter =3.0×103J/kg∘C. The falls in temperature 350 second after switching off the heater was 7.0∘C. Find the specific heat capacity of the unknown liquid in proper significant figures.
View SolutionFigure shows an electrical calorimeter to determine specific heat capacity of an unknown liquid, First of all, the mass of empty calorimeter (a copper container) is measured and suppose it is m1. Then the unknown liquid is poured in it. Now the combined mass of calorimeter+liquid system is measured and let it be m2. So the mass of liquid is (m2−m1). Initially both were at room temperature (θ0).
Now a heater is immeresed in if for time interval t. The voltage drop across the heater is V and current passing through it is I. Due to heat supplied, the temperature of both the liquid and calorimeter will rise simultaneously. After tsec, heater was switched off, and final temperature is θr. If there is no heat loss to surroundings. Heat supplied by the heater=Heat absorbed by the liquid+heat absorbed by the calorimeter (VI)t=(m2−m1)S1(θf−θ0)+m1Sc(θf−θ0)
The specific heat of the liquid S1=(VI)tθf−θ0−m1Sc(m2−m1)
Radiation correction: There can be heat loss to environment. To compensate this loss, a correction is introduced.
Let the heater was on for tsec, and then it is switched off. Now the temperature of the mixture falls due to heat loss to environment. The temperature of the mixture is measured t/2sec. after switching off. Let the fall in temperature during this time is ɛ
Now the corrected final temperature is taken as θf=θf+ɛ
If mass and specific heat capacity of calorimeter is negligible, what would be maximum permissible error in Sl. Use the date mentioned below.
m1→, Sl→0, m2=1.00kg,
V=10.0V, I=10.0A,
t=1.00×102sec, θ0=15∘C,
Corrected θ1=65∘C
View SolutionThere is a liquid of mass m and specific heat capacity c and temperature T. Another liquid of mass m2 and specific heat 2C is heated to a temperature 2T. If these two liquids are mixed, the resulting temperature of the mixture is (assume no change in the state of liquids)
View SolutionFigure shows an electrical calorimeter to determine specific heat capacity of an unknown liquid, First of all, the mass of empty calorimeter (a copper container) is measured and suppose it is m1. Then the unknown liquid is poured in it. Now the combined mass of calorimeter+liquid system is measured and let it be m2. So the mass of liquid is (m2−m1). Initially both were at room temperature (θ0).
Now a heater is immeresed in if for time interval t. The voltage drop across the heater is V and current passing through it is I. Due to heat supplied, the temperature of both the liquid and calorimeter will rise simultaneously. After tsec, heater was switched off, and final temperature is θr. If there is no heat loss to surroundings. Heat supplied by the heater=Heat absorbed by the liquid+heat absorbed by the calorimeter (VI)t=(m2−m1)S1(θf−θ0)+m1Sc(θf−θ0)
The specific heat of the liquid S1=(VI)tθf−θ0−m1Sc(m2−m1)
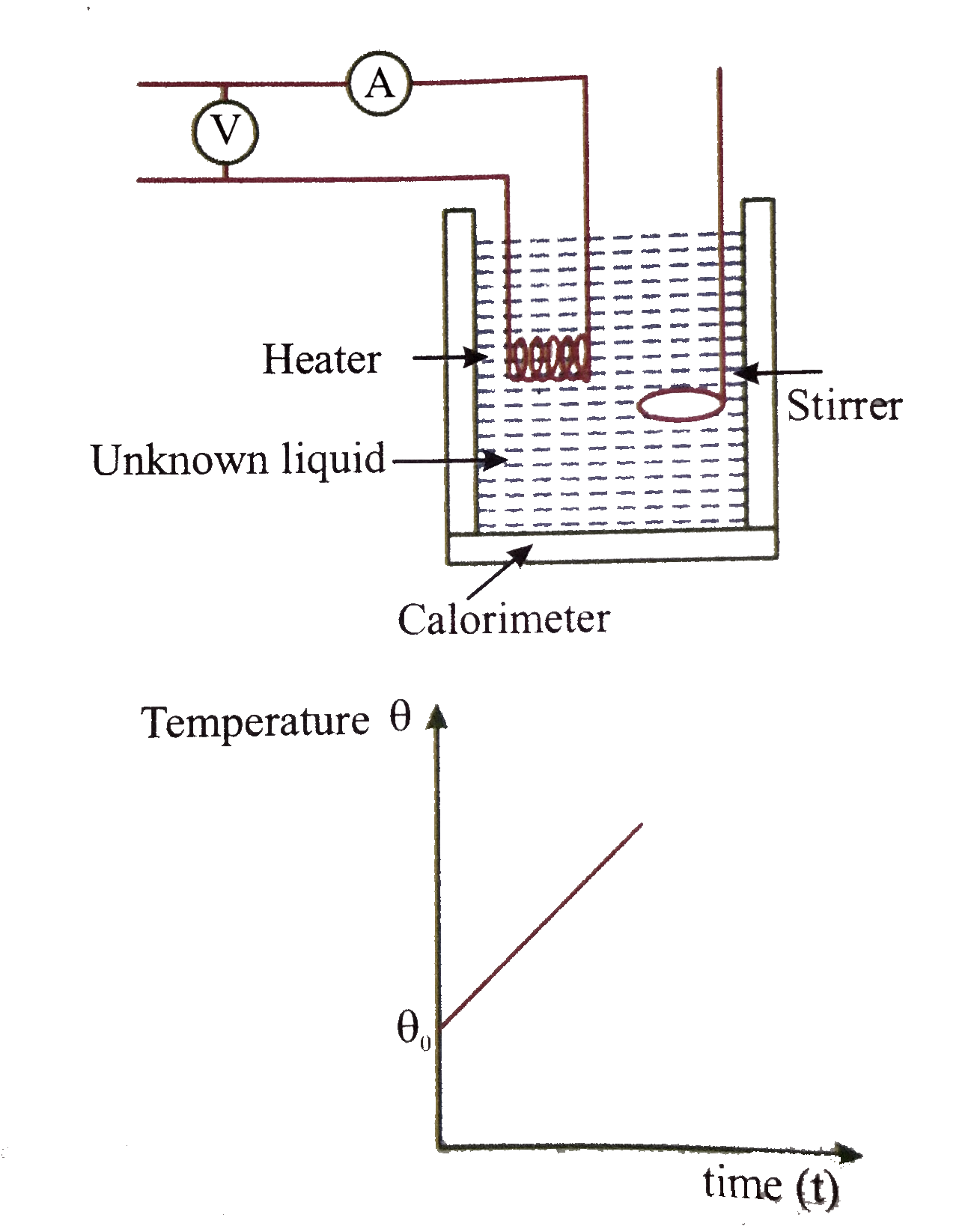
Radiation correction: There can be heat loss to environment. To compensate this loss, a correction is introduced.
Let the heater was on for tsec, and then it is switched off. Now the temperature of the mixture falls due to heat loss to environment. The temperature of the mixture is measured t/2sec. after switching off. Let the fall in temperature during this time is ɛ
Now the corrected final temperature is taken as θf=θf+ɛ
If the system were losing heat according to Newton's cooling law, the temperature of the mixture would change with time according to (while heater was on)
View Solution
