A uniform metre rule is pivoted as its mid point. A weight of 50gf is suspended at one end of it. Where should a weight of 100gf be suspended to keep the rule horizontal?
To solve the problem of where to suspend a weight of 100gf on a uniform meter rule to keep it horizontal, we can follow these steps:
1. Understanding the Setup:
- A uniform meter rule is pivoted at its midpoint (50 cm mark).
- A weight of 50gf is suspended at one end (0 cm mark).
- We need to find the position (x) from the center (50 cm) where a weight of 100gf should be suspended to balance the rule.
2. Identifying Forces and Distances:
- The force due to the 50gf weight is acting downward at the 0 cm mark.
- The distance from the pivot (50 cm) to the 0 cm mark is 50 cm.
- The force due to the 100gf weight will act downward at an unknown distance x from the pivot.
3. Setting Up the Moment Equation:
- For the rule to remain horizontal, the clockwise moment about the pivot must equal the anticlockwise moment.
- Clockwise moment due to the 50gf weight:
Moment=Force×Distance=50gf×50cm
- Anticlockwise moment due to the 100gf weight:
Moment=100gf×x
4. Equating the Moments:
- Set the clockwise moment equal to the anticlockwise moment:
50gf×50cm=100gf×x
5. Solving for x:
- Rearranging the equation gives:
x=50gf×50cm100gf
- Simplifying this:
x=2500gf⋅cm100gf=25cm
6. Conclusion:
- The weight of 100gf should be suspended 25 cm from the pivot (50 cm mark) towards the other end (75 cm mark) to keep the meter rule horizontal.
Final Answer:
The weight of 100gf should be suspended at the 75 cm mark from one end of the meter rule.
---
- A uniform meter rule is pivoted at its midpoint (50 cm mark).
- A weight of 50gf is suspended at one end (0 cm mark).
- We need to find the position (x) from the center (50 cm) where a weight of 100gf should be suspended to balance the rule.
- The force due to the 50gf weight is acting downward at the 0 cm mark.
- The distance from the pivot (50 cm) to the 0 cm mark is 50 cm.
- The force due to the 100gf weight will act downward at an unknown distance x from the pivot.
- For the rule to remain horizontal, the clockwise moment about the pivot must equal the anticlockwise moment.
- Clockwise moment due to the 50gf weight:
Moment=Force×Distance=50gf×50cm
- Anticlockwise moment due to the 100gf weight:
Moment=100gf×x
- Set the clockwise moment equal to the anticlockwise moment:
50gf×50cm=100gf×x
- Rearranging the equation gives:
x=50gf×50cm100gf
- Simplifying this:
x=2500gf⋅cm100gf=25cm
- The weight of 100gf should be suspended 25 cm from the pivot (50 cm mark) towards the other end (75 cm mark) to keep the meter rule horizontal.
The weight of 100gf should be suspended at the 75 cm mark from one end of the meter rule.
Topper's Solved these Questions
- FORCE Book:ICSEChapter:FORCE Exercise:EXERCISE 1B
Explore 11 Videos
- FORCE Book:ICSEChapter:FORCE Exercise:EXERCISE 1(B) Multiple choice questions
Explore 2 Videos
- FORCE Book:ICSEChapter:FORCE Exercise:EXERCISE 1(A) Multiple choice questions
Explore 2 Videos
- ELECTRO-MAGNETISM Book:ICSEChapter:ELECTRO-MAGNETISM Exercise:EXERCISE-10 (C) NUMERICALS
Explore 1 Video
- HOUSEHOLD CIRCUITS Book:ICSEChapter:HOUSEHOLD CIRCUITS Exercise:EXERCISE -9(B) (MULTIPLE CHOICE TYPE)
Explore 2 Videos
Similar Questions
A uniform half metre rule balances horizontally on a knife edge at 29 cm mark when a weight of 20 gf is suspended from one end.
What is the weight of the half metre rule ?
View Solutionbelow shows a uniform metre rule AB pivoted at its end A at the zero mark and supported at the other end B by a spring balance when a weight of 40kgf is suspended at its 40cm mark. This rule stays horizontal . Find the reading of the spring balance when the rule is of (i) negligible mass (ii) mass 20kg.
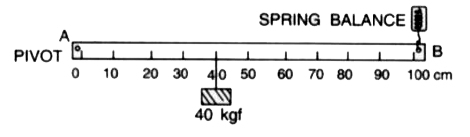
View Solution
Knowledge Check
Find the weight of half meter scale balanced at 5 cm mark when a weight of 10 gf is suspended at one of its ends.
A2.5gfB100gfC0.2gfD50gf
A uniform half metre rule balances horizontally on a knife edge at 29 cm mark when a weight of 20 gf is suspended from one end.
Draw a diagram of the arrangement.
View SolutionFig.1.33 shows a uniform metre rule placed on a fulcrum at its mid point O and having a weight 40gf at the 10cm mark and a weight of 20gf at the 90cm mark. (i) Is the metre rule in equilibrium? If not , how will the turn?
(ii) How can the rule be brought in equilibrium by using an additional weight of 40 gf?
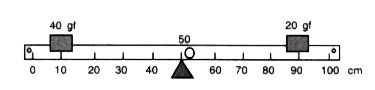
View SolutionA uniform metre rule between horizontally on a knife edge placed at the 58cm mark when a weight of 20gf is suspended from one end.
(i) Draw a diagram of the arrangement.
(ii) What is the weight of the rule?
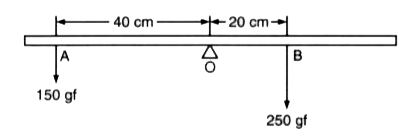
View SolutionThe diagram in Fig.1.34 shows a uniform metre rule weighing 100gf, pivoted at its centre O. Two weights 150 gf and 250 gf hang from the points A and B respectively of the metre rule such that OA= 40cm and OB=20cm . Calculate (i) the total anticlockwise moment about O, (ii) the total clockwise moment about O, (iii) the difference of anticlockwise and clockwise moments, and (iv) the distance from O where a 100gf weight should be placed to balanced the metre rule.
View SolutionA half metre rod is pivoted at the centre with two weights of 20 gf and 12 gf suspended at a perpendicular distance of 6 cm and 10 cm from the pivot respectively as shown below:
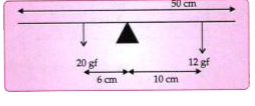
Is the rod in equilibrium ?
View SolutionA half metre rod is pivoted at the centre with two weights of 20 gf and 12 gf suspended at a perpendicular distance of 6 cm and 10 cm from the pivot respectively as shown below:
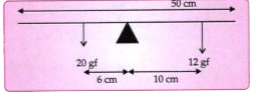
The direction of 20 kgf force is reversed. What is the magnitude of the resultant moment of the forces on the rod ?
View SolutionA half metre rod is pivoted at the centre with two weights of 20 gf and 12 gf suspended at a perpendicular distance of 6 cm and 10 cm from the pivot respectively as shown below.
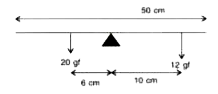
Which of the two forces acting on the rigid rod causes clockwise moment?
View Solution

