A uniform metre rule of mass 100g is balanced on a fulcrum at mark 40cm by suspending an unknown mass m at the mark 20cm.
(i) Find the value of m.
(ii) To which side the rule will tilt if the mass m is moved to the mark 10cm?
(iii) What is the resultant moment now?
(iv) How can it be balanced by another mass of 50 g?
To solve the problem step by step, we will break it down into parts as outlined in the question.
Part (i): Find the value of m.
1. Identify the forces and distances:
- The mass of the meter rule (uniform) is 100g and its center of mass is at 50cm.
- The fulcrum is at 40cm.
- An unknown mass m is suspended at 20cm.
2. Calculate the distances:
- Distance from the fulcrum to the center of mass of the meter rule: 50cm−40cm=10cm (clockwise moment).
- Distance from the fulcrum to the mass m: 40cm−20cm=20cm (anticlockwise moment).
3. Apply the principle of moments:
- The anticlockwise moment due to mass m must equal the clockwise moment due to the meter rule.
- Moment due to m: m⋅g⋅20
- Moment due to the meter rule: 100g⋅g⋅10
Setting the moments equal:
m⋅g⋅20=100⋅g⋅10
Cancel g from both sides:
m⋅20=1000
Solving for m:
m=100020=50g
Part (ii): To which side will the rule tilt if the mass m is moved to the mark 10 cm?
1. Recalculate distances:
- New distance from the fulcrum to the mass m at 10cm: 40cm−10cm=30cm (anticlockwise moment).
- Distance from the fulcrum to the center of mass of the meter rule remains 10cm (clockwise moment).
2. Determine the moments:
- Anticlockwise moment due to m: 50⋅g⋅30
- Clockwise moment due to the meter rule: 100⋅g⋅10
3. Compare the moments:
50⋅g⋅30=1500g(anticlockwise)
100⋅g⋅10=1000g(clockwise)
Since 1500g>1000g, the rule will tilt anticlockwise.
Part (iii): What is the resultant moment now?
1. Calculate the resultant moment:
- Anticlockwise moment: 50⋅g⋅30=1500g
- Clockwise moment: 100⋅g⋅10=1000g
2. Resultant moment:
Resultant moment=Anticlockwise moment−Clockwise moment
=1500g−1000g=500g
Part (iv): How can it be balanced by another mass of 50 g?
1. Set up the equation for balance:
- Let x be the distance from the fulcrum where the 50 g mass is suspended.
- The anticlockwise moment due to m at 10cm is 50⋅g⋅30.
- The clockwise moment due to the meter rule and the additional mass is:
(100⋅g⋅10)+(50⋅g⋅(x−40))
2. Set the moments equal for balance:
1500g=1000g+50g(x−40)
Simplifying:
1500=1000+50(x−40)
500=50(x−40)
10=x−40
x=50cm
Thus, to balance the meter rule, the 50 g mass should be suspended at the center (50 cm from the starting point).
- The mass of the meter rule (uniform) is 100g and its center of mass is at 50cm.
- The fulcrum is at 40cm.
- An unknown mass m is suspended at 20cm.
- Distance from the fulcrum to the center of mass of the meter rule: 50cm−40cm=10cm (clockwise moment).
- Distance from the fulcrum to the mass m: 40cm−20cm=20cm (anticlockwise moment).
- The anticlockwise moment due to mass m must equal the clockwise moment due to the meter rule.
- Moment due to m: m⋅g⋅20
- Moment due to the meter rule: 100g⋅g⋅10
m⋅g⋅20=100⋅g⋅10
Cancel g from both sides:
m⋅20=1000
Solving for m:
m=100020=50g
- New distance from the fulcrum to the mass m at 10cm: 40cm−10cm=30cm (anticlockwise moment).
- Distance from the fulcrum to the center of mass of the meter rule remains 10cm (clockwise moment).
- Anticlockwise moment due to m: 50⋅g⋅30
- Clockwise moment due to the meter rule: 100⋅g⋅10
50⋅g⋅30=1500g(anticlockwise)
100⋅g⋅10=1000g(clockwise)
Since 1500g>1000g, the rule will tilt anticlockwise.
- Anticlockwise moment: 50⋅g⋅30=1500g
- Clockwise moment: 100⋅g⋅10=1000g
Resultant moment=Anticlockwise moment−Clockwise moment
=1500g−1000g=500g
- Let x be the distance from the fulcrum where the 50 g mass is suspended.
- The anticlockwise moment due to m at 10cm is 50⋅g⋅30.
- The clockwise moment due to the meter rule and the additional mass is:
(100⋅g⋅10)+(50⋅g⋅(x−40))
1500g=1000g+50g(x−40)
Simplifying:
1500=1000+50(x−40)
500=50(x−40)
10=x−40
x=50cm
Topper's Solved these Questions
- FORCE Book:ICSEChapter:FORCE Exercise:EXERCISE 1B
Explore 11 Videos
- FORCE Book:ICSEChapter:FORCE Exercise:EXERCISE 1(B) Multiple choice questions
Explore 2 Videos
- FORCE Book:ICSEChapter:FORCE Exercise:EXERCISE 1(A) Multiple choice questions
Explore 2 Videos
- ELECTRO-MAGNETISM Book:ICSEChapter:ELECTRO-MAGNETISM Exercise:EXERCISE-10 (C) NUMERICALS
Explore 1 Video
- HOUSEHOLD CIRCUITS Book:ICSEChapter:HOUSEHOLD CIRCUITS Exercise:EXERCISE -9(B) (MULTIPLE CHOICE TYPE)
Explore 2 Videos
Similar Questions
The diagram alongside shows a uniform metre rule of weight 100 gf being balanced on a knife edge placed at the 40 cm mark, by suspending a weight w gf at the mark 20 cm, find:
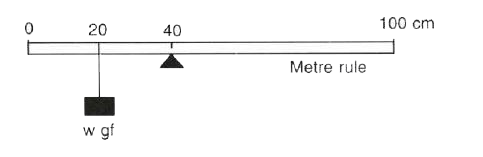
the resultant moment and its direction if the weight w is moved to the mark 30 cm.
View SolutionA uniform metre rod is balanced at the 70 cm mark by suspending a weight of 50 gf at the 40 cm mark and 200 gf at the 95 cm mark. Draw a diagram of the arrangement and calculate the weight of the metre rod.
View Solution
Knowledge Check

A rectangular thin plate of dimension 3m x 4m is balanced on the fulcrum as shown above. Find the resultant moment of force?A9Nm clockwiseB9Nm anticlockwiseC5Nm anticlockwiseD6Nm clockwise
The diagram alongside shows a uniform metre rule of weight 100 gf being balanced on a knife edge placed at the 40 cm mark, by suspending a weight w gf at the mark 20 cm, find:
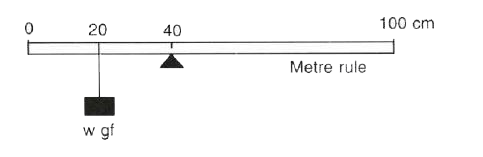
the position of another weight of 50 gf to balance the rule in part (ii).
View SolutionThe diagram alongside shows a uniform metre rule of weight 100 gf being balanced on a knife edge placed at the 40 cm mark, by suspending a weight w gf at the mark 20 cm, find:
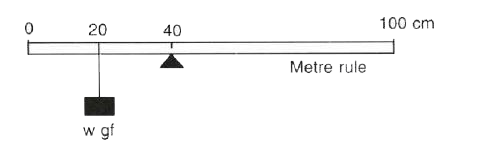
the value of w.
View SolutionA uniform metre scale can be balanced at the 70.0 cm mark when a mass of 0.05 kg is hung from the 94.0 cm mark.
Find the mass of the metre scale.
View SolutionA uniform metre scale can be balanced at the 70.0 cm mark when a mass of 0.05 kg is hung from the 94.0 cm mark.
Draw a diagram of the arrangement.
View SolutionA uniform metre rule of weight 10gf is pivoted at its 0 mark.
(i) What moment of force depresses the rule?
(ii) How can it can be made horizontal by applying a least force?
View SolutionFigure, shows a uniform metre rule of weight W supported on a fulcrum at the 60 cm mark by applying the effort E at the 90 cm mark.

(a) State with reason whether the weight W of the rule is greater than, less than or equal to the effort E.
(b) Find the mechanical advantage in a ideal case.
View SolutionA uniform half metre rule can be balanced at the 29.0cm mark when a mass 20g is hung from its one end.
(a) Draw a diagram of the arrangement
(b) Find the mass of the half metre rule.
( c) In Which direction would the balancing point shift if 20g mass is shifted inside from its one end?
View Solution

