A uniform metre scale can be balanced at the 70.0 cm mark when a mass of 0.05 kg is hung from the 94.0 cm mark.
Find the mass of the metre scale.
To solve the problem, we will use the principle of moments, which states that for an object in equilibrium, the clockwise moments about a pivot point are equal to the counterclockwise moments.
1. Identify the pivot point: The meter scale is balanced at the 70.0 cm mark. This is our pivot point.
2. Determine the center of gravity of the meter scale: Since the meter scale is uniform, its center of gravity is at the midpoint, which is at the 50.0 cm mark.
3. Identify the forces acting on the scale:
- Let the mass of the meter scale be m kg.
- A mass of 0.05 kg is hung from the 94.0 cm mark.
4. Calculate the distances from the pivot:
- The distance from the pivot (70.0 cm) to the center of gravity (50.0 cm) is:
x1=70.0cm−50.0cm=20.0cm
- The distance from the pivot (70.0 cm) to the point where the mass is hung (94.0 cm) is:
x2=94.0cm−70.0cm=24.0cm
5. Apply the principle of moments:
Clockwise moment=Counterclockwise moment
This gives us the equation:
m⋅x1=0.05kg⋅x2
Substituting the distances:
m⋅20.0=0.05⋅24.0
6. Solve for m:
m⋅20.0=0.05⋅24.0
m⋅20.0=1.2
m=1.220.0=0.06kg
7. Convert to grams:
m=0.06kg=60grams
Final Answer:
The mass of the meter scale is 60 grams.
---
- Let the mass of the meter scale be m kg.
- A mass of 0.05 kg is hung from the 94.0 cm mark.
- The distance from the pivot (70.0 cm) to the center of gravity (50.0 cm) is:
x1=70.0cm−50.0cm=20.0cm
- The distance from the pivot (70.0 cm) to the point where the mass is hung (94.0 cm) is:
x2=94.0cm−70.0cm=24.0cm
Clockwise moment=Counterclockwise moment
This gives us the equation:
m⋅x1=0.05kg⋅x2
Substituting the distances:
m⋅20.0=0.05⋅24.0
m⋅20.0=0.05⋅24.0
m⋅20.0=1.2
m=1.220.0=0.06kg
m=0.06kg=60grams
The mass of the meter scale is 60 grams.
Topper's Solved these Questions
- SAMPLE PAPER 2011BOOK - ICSECHAPTER - SAMPLE PAPER 2011EXERCISE - SECTION-II
41 Videos
- SAMPLE PAPER 2 (PHYSICAL EDUCATION)BOOK - ICSECHAPTER - SAMPLE PAPER 2 (PHYSICAL EDUCATION)EXERCISE - MULTIPLE CHOICE QUESTIONS
50 Videos
- SAMPLE PAPER 2012BOOK - ICSECHAPTER - SAMPLE PAPER 2012EXERCISE - SECTION-II
43 Videos
Similar Questions
A uniform metre scale can be balanced at the 70.0 cm mark when a mass of 0.05 kg is hung from the 94.0 cm mark.
Draw a diagram of the arrangement.
View SolutionA uniform half metre rule can be balanced at the 29.0cm mark when a mass 20g is hung from its one end.
(a) Draw a diagram of the arrangement
(b) Find the mass of the half metre rule.
( c) In Which direction would the balancing point shift if 20g mass is shifted inside from its one end?
View Solution
Knowledge Check
Find the weight of half meter scale balanced at 5 cm mark when a weight of 10 gf is suspended at one of its ends.
A2.5gfB100gfC0.2gfD50gfIf the centre of gravity of a metre scale of mass 80g lies at the 45 cm mark, then which one of the following diagrams will show the balanced position of the scale.
A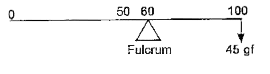 B
B C
C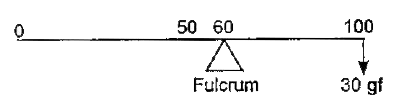 D
D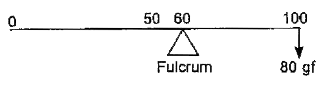
A uniform metre rule rests horizontally on a knife edge at the 60cm mark when a mass of 10g is suspended from one end. Draw a diagram of the arrangement.
(a) At which end must this mass be suspended
(b) What is the mass of the rule?
(c ) THe 10g mass is now shifted to the 90cm mark. In which direction must the knife edge be shifted to make the rule horizontal again?
View SolutionA uniform metre rod is balanced at the 70 cm mark by suspending a weight of 50 gf at the 40 cm mark and 200 gf at the 95 cm mark. Draw a diagram of the arrangement and calculate the weight of the metre rod.
View SolutionA uniform meter scale is kept in equilibrium when supported at the 60 cm mark and a mass weight of the scale is greater than, less than or equal to the weight of mass M.
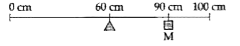
View SolutionA uniform half metre rule balances horizontally on a knife edge at 29 cm mark when a weight of 20 gf is suspended from one end.
What is the weight of the half metre rule ?
View SolutionA uniform thermometre scale is at steady state with its 0 cm mark at 20°C and 100 cm mark at 100°C. Temperature of the 60 cm mark is-
View SolutionA uniform metre scale is in equilibrium position. Calculate the mass of the ruler.

View Solution
