When a boy weighing 20 kgf sits at one end of a 4m long see saw, if gets depressed at this end. How can it be brought to the horizontal position by a man weighing 40 kgf.
To solve the problem of balancing the seesaw, we can follow these steps:
Step 1: Understand the Problem
We have a seesaw that is 4 meters long, with a boy weighing 20 kgf sitting at one end. We need to find out where a man weighing 40 kgf should sit to bring the seesaw back to a horizontal position.
Step 2: Identify the Moments
The moment (or torque) is calculated as the product of the force and the distance from the pivot point (fulcrum).
- The boy creates a moment about the pivot point:
- Weight of the boy = 20 kgf
- Distance from the center of the seesaw to the boy = 2 meters (since the seesaw is 4 meters long, the center is at 2 meters).
Moment created by the boy:
Momentboy=Weightboy×Distanceboy=20kgf×2m=40kgf m
Step 3: Set Up the Equation for the Man
Let x be the distance from the center of the seesaw where the man should sit. The moment created by the man is:
- Weight of the man = 40 kgf
- Distance from the center = x
Moment created by the man:
Momentman=Weightman×Distanceman=40kgf×x
Step 4: Equate the Moments
For the seesaw to be balanced, the moments must be equal:
Momentboy=Momentman
Substituting the values we have:
40kgf m=40kgf×x
Step 5: Solve for x
Now, we can solve for x:
x=40kgf m40kgf=1m
Conclusion
The man should sit 1 meter from the center of the seesaw to bring it back to a horizontal position.
---
We have a seesaw that is 4 meters long, with a boy weighing 20 kgf sitting at one end. We need to find out where a man weighing 40 kgf should sit to bring the seesaw back to a horizontal position.
The moment (or torque) is calculated as the product of the force and the distance from the pivot point (fulcrum).
- Weight of the boy = 20 kgf
- Distance from the center of the seesaw to the boy = 2 meters (since the seesaw is 4 meters long, the center is at 2 meters).
Moment created by the boy:
Momentboy=Weightboy×Distanceboy=20kgf×2m=40kgf m
Let x be the distance from the center of the seesaw where the man should sit. The moment created by the man is:
- Weight of the man = 40 kgf
- Distance from the center = x
Momentman=Weightman×Distanceman=40kgf×x
For the seesaw to be balanced, the moments must be equal:
Momentboy=Momentman
Substituting the values we have:
40kgf m=40kgf×x
Now, we can solve for x:
x=40kgf m40kgf=1m
The man should sit 1 meter from the center of the seesaw to bring it back to a horizontal position.
Topper's Solved these Questions
- FORCE Book:ICSEChapter:FORCE Exercise:EXERCISE 1B
Explore 11 Videos
- FORCE Book:ICSEChapter:FORCE Exercise:EXERCISE 1(B) Multiple choice questions
Explore 2 Videos
- FORCE Book:ICSEChapter:FORCE Exercise:EXERCISE 1(A) Multiple choice questions
Explore 2 Videos
- ELECTRO-MAGNETISM Book:ICSEChapter:ELECTRO-MAGNETISM Exercise:EXERCISE-10 (C) NUMERICALS
Explore 1 Video
- HOUSEHOLD CIRCUITS Book:ICSEChapter:HOUSEHOLD CIRCUITS Exercise:EXERCISE -9(B) (MULTIPLE CHOICE TYPE)
Explore 2 Videos
Similar Questions
A uniform seesaw, 5m long, is supported at its centre. A boy weighing 40 kgf sits at a distance of 1 m from the centre of the seesaw.
(i) To which class of lever does it belong ?
(ii) Find where a girl of weight 20 kgf must sit on the seesaw so as the balance the weight of the boy.
View SolutionA thin bar of mass M and length L is free to rotate about a fixed horizontal axis through a point at its end. The bar is brought to a horizontal position and then released. The axis is perpendicular to the rod. The angular velocity when it reaches the lowest point is
View SolutionA thin bar of mass m and length l is free to rotate about a fixed horizontal axis through a point at its end.The bar is brought to a horizontal position. (θ=90∘) and then released. The angular velocity when it reaches the lowest point is
View SolutionThere is an insulator rod of length L and of negligible mass with two small balls of mass m and electric charge Q attached to its ends. The rod can rotate in the horizontal plane around a vertical axis crossing it ata distance L/4 from one of its ends.
At first the rod is in unstabele equillbrium in a Horizontal uniform electric field of field strenght E. Then we gently displace it from this position. Determine the maximim velocity attained by the ball taht is closer to the axis in the subsequent motion
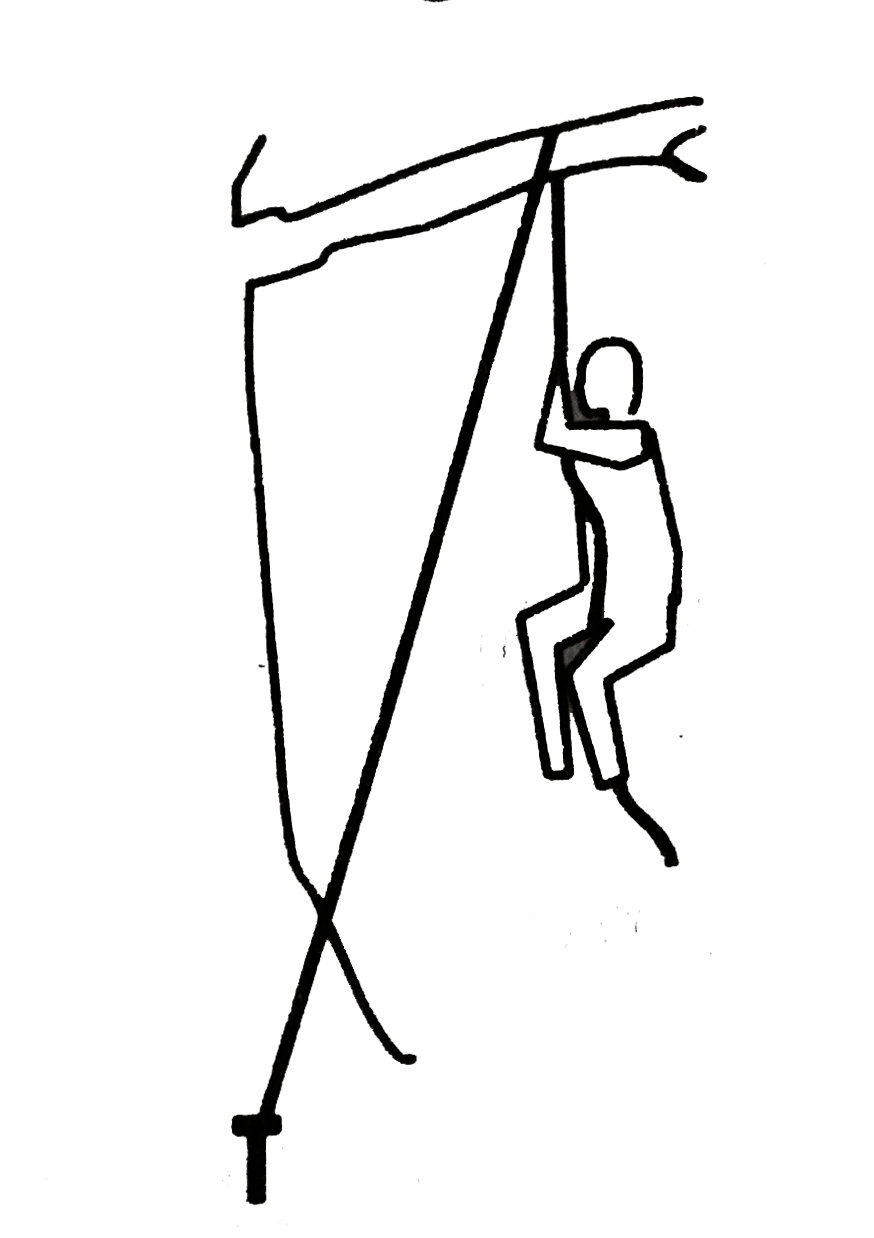
View SolutionA light rope fixed at one end of a wooden clamp on the ground passes over a tree branch and hangs on the other side. It makes an angle of 300 with the ground. A man weighing (60 kg) wants to climb up the rope. The wooden clamp can come out of the ground if an upward force greater than 360 N is applied it. Find the maximum acceleration in the upward direction with which the man can climb safely. Neglect friction at the tree branch. Take g=10ms2
View SolutionA uniform rod of mass m and length l is fixed from Point A, which is at a distance l/4 from one end as shown in the figure. The rod is free to rotate in a vertical plane. The rod is released from the horizontal position.

What is the reaction at the hinge, when kinetic energy of the rod is maximum?
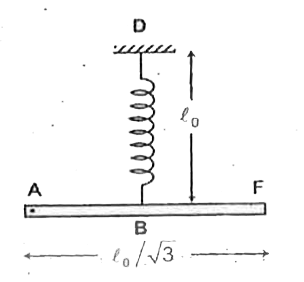
View SolutionIn the figure shown one end of a light spring of natural length l0=√58m(≈0.8m) is fixed at point D and other end is attached to the centre B of a uniform rod AF of length l0/√3 and mass 10kg. The rod is free to rotate in a vertical plane about a fixed horizontal axis passing through the end A of the rod. The rod is held at rest in horizontal position and the spring is in relaxed state. It is found that, when the rod is released to move it makes an angle of 60∘ with the horizontal when it comes to rest for the first time. Find the
(a) the maximum elogation in the spring . (Approximately)
(b) the spring constant. (Approximately)
View SolutionA body weighing 13 kg is suspended by two strings 5 m and 12 m long, their other ends being fastened to the extremities of a rod 13 m long. If the rod be so held that the body hangs immediately below the middle point. The tensions in the strings are (1) 12 kg and 13 kg (2) 5 kg and 5 kg (3) 5 kg and 12 kg (4) 5 kg and 13 kg
View SolutionA massless stick of length L is hinged at one end and a mass m attached to its other end. The stick is free to rotate in vertical plane about a fixed horizontal axis passing through frictionless hinge. The stick is held in a horizontal position. At what distance x from the hinge should a second mass M = m be attached to the stick, so that stick falls as fast as possible when released from rest

View SolutionIn the figure shown, the cart of mass 6m is initially at rest. A particle of mass in is attached to the end of the light rod which can rotate freely about A. If the rod is released from rest in a horizontal position shown, determine the velocity vrel of the particle with respect to the cart when the rod is vertical.

View Solution