A sphere of mass 50 gm and diameter 2 cm rolls without slipping with a velocfty of 5 cm/s. Calculate the total energy.
To calculate the total energy of a rolling sphere, we need to consider both its translational and rotational kinetic energy. Here’s a step-by-step solution:
Step 1: Identify the given values
- Mass of the sphere, m=50g=0.05kg
- Diameter of the sphere, d=2cm (which gives a radius r=d2=1cm=0.01m)
- Velocity of the sphere, v=5cm/s=0.05m/s
Step 2: Calculate the translational kinetic energy
The translational kinetic energy (KEtrans) is given by the formula:
KEtrans=12mv2
Substituting the values:
KEtrans=12×0.05kg×(0.05m/s)2
KEtrans=12×0.05×0.0025
KEtrans=12×0.000125=0.0000625J=6.25×10−5J
Step 3: Calculate the moment of inertia of the sphere
The moment of inertia (I) for a solid sphere is given by:
I=25mr2
Substituting the values:
I=25×0.05kg×(0.01m)2
I=25×0.05×0.0001
I=2×0.000015=8×10−6kg m2
Step 4: Calculate the angular velocity (ω)
Since the sphere rolls without slipping, we can relate the linear velocity v to the angular velocity ω using the formula:
v=rω⟹ω=vr
Substituting the values:
ω=0.05m/s0.01m=5rad/s
Step 5: Calculate the rotational kinetic energy
The rotational kinetic energy (KErot) is given by:
KErot=12Iω2
Substituting the values:
KErot=12×8×10−6kg m2×(5rad/s)2
KErot=12×8×10−6×25
KErot=4×10−5J
Step 6: Calculate the total energy
The total energy (Etotal) is the sum of the translational and rotational kinetic energies:
Etotal=KEtrans+KErot
Substituting the values:
Etotal=6.25×10−5J+4×10−5J
Etotal=10.25×10−5J=1.025×10−4J
Final Answer
The total energy of the sphere is 1.025×10−4J.
---
- Mass of the sphere, m=50g=0.05kg
- Diameter of the sphere, d=2cm (which gives a radius r=d2=1cm=0.01m)
- Velocity of the sphere, v=5cm/s=0.05m/s
The translational kinetic energy (KEtrans) is given by the formula:
KEtrans=12mv2
Substituting the values:
KEtrans=12×0.05kg×(0.05m/s)2
KEtrans=12×0.05×0.0025
KEtrans=12×0.000125=0.0000625J=6.25×10−5J
The moment of inertia (I) for a solid sphere is given by:
I=25mr2
Substituting the values:
I=25×0.05kg×(0.01m)2
I=25×0.05×0.0001
I=2×0.000015=8×10−6kg m2
Since the sphere rolls without slipping, we can relate the linear velocity v to the angular velocity ω using the formula:
v=rω⟹ω=vr
Substituting the values:
ω=0.05m/s0.01m=5rad/s
The rotational kinetic energy (KErot) is given by:
KErot=12Iω2
Substituting the values:
KErot=12×8×10−6kg m2×(5rad/s)2
KErot=12×8×10−6×25
KErot=4×10−5J
The total energy (Etotal) is the sum of the translational and rotational kinetic energies:
Etotal=KEtrans+KErot
Substituting the values:
Etotal=6.25×10−5J+4×10−5J
Etotal=10.25×10−5J=1.025×10−4J
The total energy of the sphere is 1.025×10−4J.
Topper's Solved these Questions
- CIRCULAR MOTION Book:ICSEChapter:CIRCULAR MOTION Exercise:MODULE 1 (CONCEPTUAL SHORT ANSWERS QUESTIONS WITH ANSWERS )
Explore 11 Videos
- CIRCULAR MOTION Book:ICSEChapter:CIRCULAR MOTION Exercise:MODULE 1 (LONG ANSWER QUESTIONS)
Explore 8 Videos
- COMPETITION CARE UNITBook:ICSEChapter:COMPETITION CARE UNITExercise:OBJECTIVE QUESTIONS FROM PREVIOUS IAS EXAMINATIONS
Explore 50 Videos
Similar Questions
If a solid sphere of mass 1 kg and radius 0.1 m rolls without slipping at a uniform velocity of 1 m/s along a straight line on a horizontal floor, the kinetic energy is
View SolutionA circular disc of mass 2 kg and radius 10 cm rolls without slipping with a speed 2 m/s. The total kinetic energy of disc is
View SolutionA hollow sphere of mass m starting from rest rolls without slipping, on an inclined plane of inclination What is the total energy of the sphere after 10−5s if after 10−5isv?
View SolutionA uniform sphere of mass m and radius R rolls without slipping down an inclined plane set at an angle θ to the horizontal. Find
(a) the friction coefficient at which slipping is absent,
(b) the kinetic energy of the sphere t seconds after the beginning of motion.
View SolutionA loop and a disc have same mass and roll without slipping with the same linear velocity v. If the total kinetic energy of the loop is 8J, the kinetic energy of the disc must be.
View SolutionA uniform thin ring of mass 0.4kg rolls without slipping on a horizontal surface with a linear velocity of 10 cm/s. The kinetic energy of the ring is
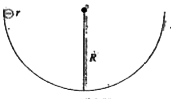
View SolutionThe radius of a large hemisphere whose" axis of symmetry is vertical is R = 50 cm. A small sphere of radius r= 5cm rolls without slipping with a speed of 2cm/s. The mass of the sphere is 100 gm. If it start's at the top from rest (i) what is the kinetic energy at the bottom? (ii) What fraction is rotational ? (iii) What fraction is translational?
View SolutionA sphere of mass m and radius r rolls on a horizontal plane without slipping with a speed u. Now it rolls up vertically, then maximum height it would be attain will be
View Solution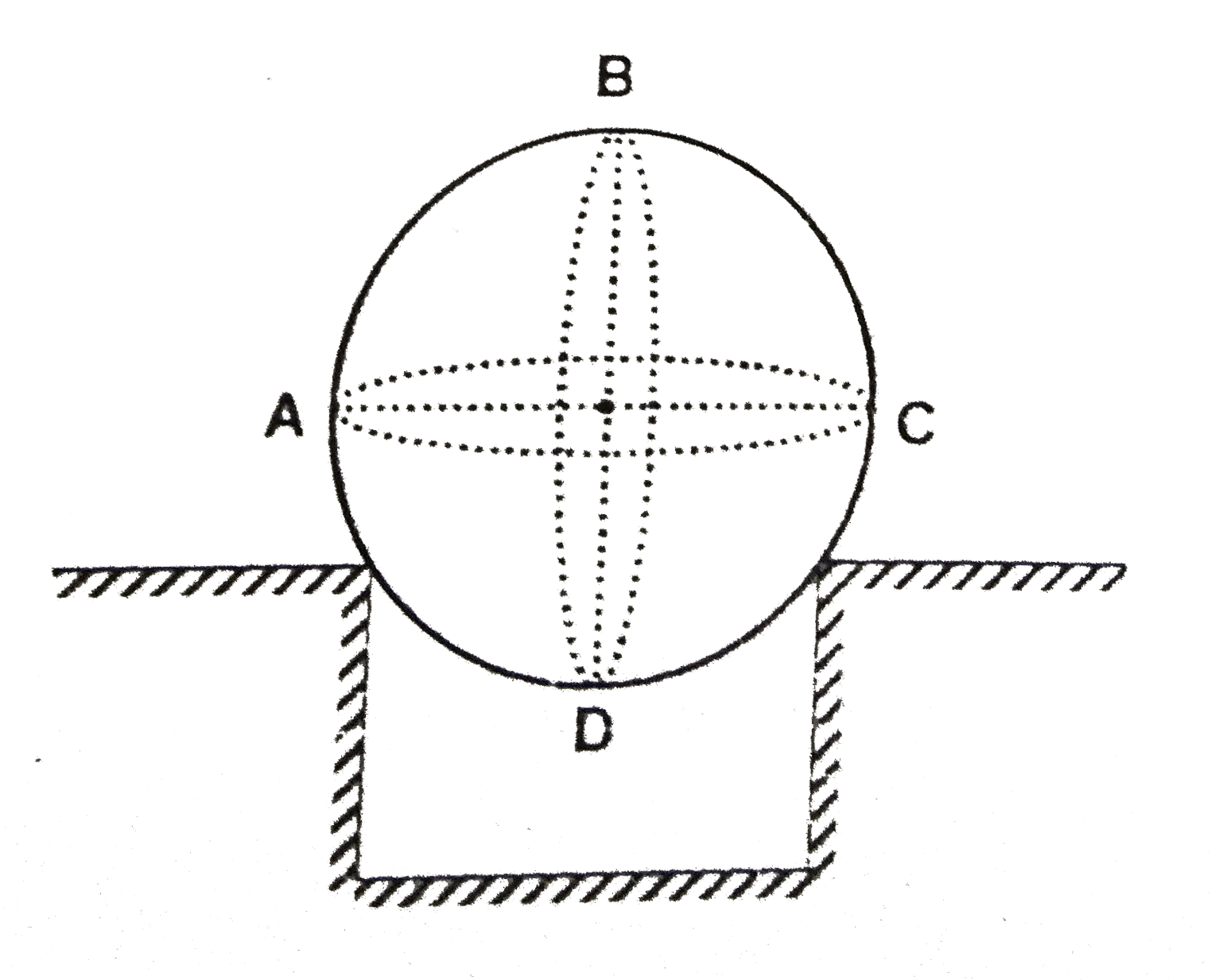
A sphere of mass m and radius r rolls without slipping over a tunnel of width d=8r5 as shown in the figure. (in the figure the sphere rolls perpendicular to the plane of the page) the velocity of centre of mass of sphere is v directed into the plane of the page. the maximum speed of a point on the sphere is
View SolutionA disc of mass 5 kg and radius 50 cm rolls on the ground at the rate of 10ms−1. Calculate the K.E. of the disc.
View Solution

