The midpoints of alternating sides of a regular octagon are joined to form a square. If each side of the octagon is a, find each side of the square.
(2+√2)a2
(4+√2)a2
2(1+√2)a√2
(2+√2)a
The correct Answer is:A
To find the side of the square formed by joining the midpoints of alternating sides of a regular octagon, we can follow these steps:
Step 1: Understand the Geometry of the Octagon
A regular octagon has 8 equal sides. Let's denote the length of each side as a.
Step 2: Identify the Midpoints
The midpoints of the alternating sides of the octagon will be selected. For an octagon with vertices labeled A1,A2,A3,…,A8, we will take the midpoints of sides A1A2, A3A4, A5A6, and A7A8.
Step 3: Calculate the Length of the Midpoints
Since the octagon is regular, the distance between two midpoints of alternating sides can be calculated. The distance between two midpoints (say M1 and M2) can be determined using the properties of right triangles.
Step 4: Form a Right Triangle
Consider one of the triangles formed by the midpoints. The angle between the sides of the octagon at the vertices is 45∘ (since 360∘/8=45∘). The line connecting the midpoints will form a right triangle with the sides of the octagon.
Step 5: Use Pythagorean Theorem
Let’s denote the distance between two adjacent midpoints as PQ. In triangle PQR:
- PR (the distance between two midpoints) is a2.
- The height from the midpoint to the base is also a2.
Using the Pythagorean theorem:
PQ2+PR2=QR2
Substituting the values:
PQ2+(a2)2=(a√2)2
This simplifies to:
PQ2+a24=a22
Thus,
PQ2=a22−a24=a24
Step 6: Solve for PQ
Taking the square root gives us:
PQ=a2√2=a√24
Step 7: Find the Side of the Square
The side of the square formed by the midpoints is equal to a+2PQ:
Side of the square=a+2(a√24)=a+a√22
Factoring out a:
Side of the square=a(1+√22)
Final Result
Thus, the side of the square formed by joining the midpoints of alternating sides of a regular octagon is:
Side of the square=a(1+√22)
A regular octagon has 8 equal sides. Let's denote the length of each side as a.
The midpoints of the alternating sides of the octagon will be selected. For an octagon with vertices labeled A1,A2,A3,…,A8, we will take the midpoints of sides A1A2, A3A4, A5A6, and A7A8.
Since the octagon is regular, the distance between two midpoints of alternating sides can be calculated. The distance between two midpoints (say M1 and M2) can be determined using the properties of right triangles.
Consider one of the triangles formed by the midpoints. The angle between the sides of the octagon at the vertices is 45∘ (since 360∘/8=45∘). The line connecting the midpoints will form a right triangle with the sides of the octagon.
Let’s denote the distance between two adjacent midpoints as PQ. In triangle PQR:
- PR (the distance between two midpoints) is a2.
- The height from the midpoint to the base is also a2.
PQ2+PR2=QR2
Substituting the values:
PQ2+(a2)2=(a√2)2
This simplifies to:
PQ2+a24=a22
Thus,
PQ2=a22−a24=a24
Taking the square root gives us:
PQ=a2√2=a√24
The side of the square formed by the midpoints is equal to a+2PQ:
Side of the square=a+2(a√24)=a+a√22
Factoring out a:
Side of the square=a(1+√22)
Thus, the side of the square formed by joining the midpoints of alternating sides of a regular octagon is:
Side of the square=a(1+√22)
Topper's Solved these Questions
Similar Questions
Knowledge Check
If each side of the octagon is a, find the area of the octagon.
A2(√2−1)a2B4(1+√2)a2C2(2+√2)a2D2(1+√2)a2The measure of each interior angle of a regular octagon is
A135∘B125∘C115∘D120∘If the apothem of a regular hexagon is a, find each side of the hexagon.
AA)3a√2BB)√3aCC)0.67aDD)2√3a
The side of a given square is 10 cm. The midpoints of its sides are joined to form a new square. Again, the midpoints of the sides of this new aquare are joined to form another square. The process is continued indefinitely. Find (i) the sum of the areas and (ii) the sum of the perimeters of the squares.
View SolutionIn the given figure a quadrilateral is formed by joining the alternate vertices of a regular octagon. If the area of the octagon be 2(√2−1)sq cm, find the area of the square.

View SolutionIf each side of the octagon be a, then find the longest diagonal of the octagon.
View SolutionIf each side of the octagon be a, then find the shortest diagonal of the octagon.
View SolutionFind the area of shaded portion if each side of the square is 14 cm.
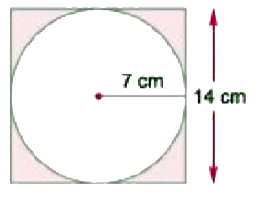
View Solution
