If each side of the octagon is a, find the area of the octagon.
2(√2−1)a2
4(1+√2)a2
2(2+√2)a2
2(1+√2)a2
The correct Answer is:D
To find the area of a regular octagon where each side is of length a, we can use the formula for the area of a regular octagon:
Area=2(1+√2)a2
1. Identify the formula for the area of a regular octagon:
The area A of a regular octagon can be expressed as:
A=2(1+√2)a2
2. Substitute the value of a:
Since each side of the octagon is given as a, we can directly substitute a into the formula:
A=2(1+√2)a2
3. Simplify the expression:
The expression 1+√2 is a constant, so we can keep it as is. The area in terms of a is:
A=2(1+√2)a2
4. Final expression:
Thus, the area of the octagon in terms of side length a is:
A=2(1+√2)a2
The area A of a regular octagon can be expressed as:
A=2(1+√2)a2
Since each side of the octagon is given as a, we can directly substitute a into the formula:
A=2(1+√2)a2
The expression 1+√2 is a constant, so we can keep it as is. The area in terms of a is:
A=2(1+√2)a2
Thus, the area of the octagon in terms of side length a is:
A=2(1+√2)a2
Topper's Solved these Questions
Similar Questions
In the given figure a quadrilateral is formed by joining the alternate vertices of a regular octagon. If the area of the octagon be 2(√2−1)sq cm, find the area of the square.

View SolutionThe corners of a square of side 'a' are cut away so as to form a regular octagon. What is the side of the octagon ?
View Solution
Knowledge Check
Neither it's the longest one nor it's the shortest one of the lengths of the diagonal of an octagon you know is d and each side of the same octagon is s, find the area of the octagon in terms of the side and the known diagonal of the regular octagon.
A3d2−√3s2Bd2−s2C2dsDBOTH (B) AND (C)The midpoints of alternating sides of a regular octagon are joined to form a square. If each side of the octagon is a, find each side of the square.
A(2+√2)a2B(4+√2)a2C2(1+√2)a√2D(2+√2)aIf each side of the octagon be a, then find the shortest diagonal of the octagon.
AA)(√2+√2)aBB)(1+√2)aCC)2(1+√2)aDD)(√4+2√2)a
Inside a unit square, all isosceles triangles whose base is a side of the square and whose vertex is the midpoint of the opposite side are drawn. If the area of the octagon determined by the intersection of these four triangles is 1λ (where λ∈N) then find the value of λ
View SolutionTop surface of a raised platform is in the shape of a regular octagon as shown in the figure. Find the area of the octagonal surface.
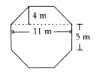
View SolutionIf each side of the octagon be a, then find the longest diagonal of the octagon.
View SolutionIf the side of an square is a, then find the side of the regular octagon that can be inscribed in this square.
View SolutionTop surface of a raised plateform is in the shape of a regular octagon as shown in the figure.
Find the area of the octagonal surface.
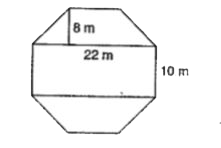
View Solution
