Triangle ABC inscribes a circle with centre O and inradius √6cm. The inradius OD divides side BC at D, such that BD=2 cm and DC=8 cm. Find the ratio AB:AC.
4:7
5:7
4:5
cannot be determined
The correct Answer is:A
Step by step video, text & image solution for Triangle ABC inscribes a circle with centre O and inradius sqrt6 cm. The inradius OD divides side BC at D, such that BD=2 cm and DC=8 cm. Find the ratio AB:AC. by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
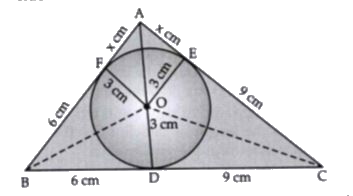
In figure , a triangle ABC is drawn to circumscribe a circle of radius 3 cm , such that segments BD and DC are of length 6 cm and 9 cm .If the area of △ABC=54cm2, then find the lengths of the side AB and AC.
View SolutionIn a triangle ABC the angle A is twice the angle C, the side BC is 2 cm longer than the side AB, and AC=5 cm. Find AB and BC.
View Solution
Knowledge Check
A ABC is inscribed in a circle with centre o and radius 5 cm and AC is a diameter of the circle. If AB = 8 cm, then BC = ......... cm.
A10B8C6D15A circle of radius 4 cm is inscribed in ΔABC, which touches side BC at D. If BD = 6 cm, DC = 8 cm then
Athe triangle is necessarily acute angledBtan.A2=47Cperimeter of the triangle ABC is 42 cmDarea of ΔABC is 84cm2In the triangle ABC, the internal bisector of angle A meets the side BC at D. If BD=7.5 cm and BC=9 cm. Then calculate the value of AB:AC.
A2 :1B1 :2C5 :1D1 :3
Perimeter of a Δ is 32 cm & inradius is 3 cm. Find the area of Δ.
View SolutionThe sides of a Δ are consecutive intergers and inradius is 4 cm. Find the area of the Δ .
View SolutionIn a ΔABC,AB=5,AC=6cm,BC=8cm . Find the length of median AD.
View Solution△ABC is an isosceles triangle with AB=AC=15cm and altitude from A to BC is 12 cm. The length of sides BC is :
View SolutionIn Δ ABC, AB = 6 cms, BC = 10 cms, AC = 8cm and ADI_BC. Find the value of the ratio of BD:DC.
View Solution
