Answer the following questions based on the information given below.
A circle with centre O and radius 2 cm inscribes a triangle ABC. Two tangents AD and BD are drawn from a point D outside the circle anf .
Find the area of , in .
4
none of these
The correct Answer is:A
To find the area of the quadrilateral OADB, we will break down the problem step by step.
Step 1: Understand the Geometry
We have a circle with center O and radius 2 cm. The tangents AD and BD are drawn from point D outside the circle, and we know that angle ABD = 60 degrees.
Step 2: Identify Key Angles
Since AD and BD are tangents to the circle from point D, the angles between the radius and the tangent at points A and B are both 90 degrees. Therefore:
- Angle OAD = 90 degrees
- Angle OBD = 90 degrees
Step 3: Calculate Angle AOB
Using the angle sum property in triangle ABD:
- Angle ADB = 180 - (Angle ABD + Angle BAD)
- Since AD = BD (tangents from the same point), Angle BAD = Angle ABD = 60 degrees.
- Therefore, Angle ADB = 180 - (60 + 60) = 60 degrees.
Now, we can find Angle AOB:
- Angle AOB = Angle AOD + Angle BOD = 60 + 60 = 120 degrees.
Step 4: Use the Law of Cosines in Triangle AOB
We can use the Law of Cosines to find the length of AB:
- AB² = OA² + OB² - 2 * OA * OB * cos(Angle AOB)
- Since OA = OB = 2 cm (the radius), we have:
AB²=2²+2²−2∗2∗2∗cos(120∘)
- cos(120 degrees) = -1/2, so:
AB²=4+4+4=12⟹AB=2√3 cm
Step 5: Calculate the Area of Triangle ADB
Since triangle ADB is isosceles with AB = 2√3 cm and angle ADB = 60 degrees, we can find the area using the formula:
Area=12×base×height
To find the height, we can drop a perpendicular from D to AB, which bisects AB since triangle ADB is isosceles. The height can be calculated as:
- Height = AB⋅sin(60∘)=2√3⋅√32=3 cm
Thus, the area of triangle ADB is:
AreaADB=12×AB×height=12×2√3×3=3√3 cm2
Step 6: Calculate the Area of Triangle OAB
Now we calculate the area of triangle OAB:
AreaOAB=12×OA×OB×sin(AngleAOB)
- OA = OB = 2 cm and Angle AOB = 120 degrees:
AreaOAB=12×2×2×sin(120∘)=12×4×√32=√3 cm2
Step 7: Calculate the Area of Quadrilateral OADB
Finally, we can find the area of quadrilateral OADB by adding the areas of triangles ADB and OAB:
AreaOADB=AreaADB+AreaOAB=3√3+√3=4√3 cm2
Final Answer
The area of quadrilateral OADB is 4√3 cm2.
---
We have a circle with center O and radius 2 cm. The tangents AD and BD are drawn from point D outside the circle, and we know that angle ABD = 60 degrees.
Since AD and BD are tangents to the circle from point D, the angles between the radius and the tangent at points A and B are both 90 degrees. Therefore:
- Angle OAD = 90 degrees
- Angle OBD = 90 degrees
Using the angle sum property in triangle ABD:
- Angle ADB = 180 - (Angle ABD + Angle BAD)
- Since AD = BD (tangents from the same point), Angle BAD = Angle ABD = 60 degrees.
- Therefore, Angle ADB = 180 - (60 + 60) = 60 degrees.
- Angle AOB = Angle AOD + Angle BOD = 60 + 60 = 120 degrees.
We can use the Law of Cosines to find the length of AB:
- AB² = OA² + OB² - 2 * OA * OB * cos(Angle AOB)
- Since OA = OB = 2 cm (the radius), we have:
AB²=2²+2²−2∗2∗2∗cos(120∘)
- cos(120 degrees) = -1/2, so:
AB²=4+4+4=12⟹AB=2√3 cm
Since triangle ADB is isosceles with AB = 2√3 cm and angle ADB = 60 degrees, we can find the area using the formula:
Area=12×base×height
To find the height, we can drop a perpendicular from D to AB, which bisects AB since triangle ADB is isosceles. The height can be calculated as:
- Height = AB⋅sin(60∘)=2√3⋅√32=3 cm
AreaADB=12×AB×height=12×2√3×3=3√3 cm2
Now we calculate the area of triangle OAB:
AreaOAB=12×OA×OB×sin(AngleAOB)
- OA = OB = 2 cm and Angle AOB = 120 degrees:
AreaOAB=12×2×2×sin(120∘)=12×4×√32=√3 cm2
Finally, we can find the area of quadrilateral OADB by adding the areas of triangles ADB and OAB:
AreaOADB=AreaADB+AreaOAB=3√3+√3=4√3 cm2
The area of quadrilateral OADB is 4√3 cm2.
Topper's Solved these Questions
Similar Questions
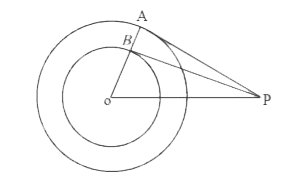
In the given figure two concentric circles with centre O are of radii 5 cm and 3 cm. From an external point P, tangents PA and PB are drawn to these circles. If AP =12 cm find BP.

View SolutionFind the length of the tangent to a circle with centre O and radius 6cm from a point P such that OP=10cm?
View Solution
Knowledge Check
Answer the following questions based on the information given below.
A circle with centre O and radius 2 cm inscribes a triangle ABC. Two tangents AD and BD are drawn from a point D outside the circle anf ∠ABD=60∘.
Find the area of □OADB, in cm2.A6√3B8√3C14√3Dnone of theseTwo tangents are drawn from a point P to a circle at A and B. O is the centre of the circle. If ∠AOP=60∘, then ∠APB is
A120∘B90∘C60∘D30∘Triangle ABC inscribes a circle with centre O and inradius √6cm. The inradius OD divides side BC at D, such that BD=2 cm and DC=8 cm. Find the ratio AB:AC.
A4:7B5:7C4:5Dcannot be determined
Two concentric circle with centre O are of radii 6 cm and 3 cm. From an external point P, tangents PA and PB are drawn to these circle as shown in the figure. If AP = 10 cm. Find BP
View SolutionTwo tangents are drawn from a point P on the circle at point A and B. O is the centre of the circle. If ∠AOP=60∘ then find ∠APB.
View SolutionFrom a point P which is at a distance of 13 cm from the centre O of a circle of radius 5 cm, the pair of tangents PQ and PR to the circle are drawn. Find the area of quadrilateral PQOR,
View SolutionA point P is at a distance of 29cm from the centre of a circle of radius 20cm. Find the length of the tangent drawn from P to the circle.
View SolutionA point P is 13 xm from the centre of a circle . Radius of the circle is 5 cm . A tangent is drawn from point P to the circle , then the length of the tangent is :
View Solution
