A point P is 13 xm from the centre of a circle . Radius of the circle is 5 cm . A tangent is drawn from point P to the circle , then the length of the tangent is :
10
11
12
13
The correct Answer is:C
To find the length of the tangent drawn from point P to the circle, we can use the following steps:
Step 1: Identify the given values
- Distance from point P to the center of the circle (OP) = 13 cm
- Radius of the circle (r) = 5 cm
Step 2: Use the tangent-segment theorem
According to the tangent-segment theorem, the length of the tangent (PT) from point P to the circle can be calculated using the formula:
PT=√OP2−r2
where:
- OP is the distance from point P to the center of the circle,
- r is the radius of the circle.
Step 3: Substitute the values into the formula
Substituting the known values into the formula:
PT=√(13)2−(5)2
Step 4: Calculate the squares
Calculating the squares:
PT=√169−25
Step 5: Perform the subtraction
Now, perform the subtraction:
PT=√144
Step 6: Calculate the square root
Finally, calculate the square root:
PT=12cm
Thus, the length of the tangent from point P to the circle is 12 cm.
---
- Distance from point P to the center of the circle (OP) = 13 cm
- Radius of the circle (r) = 5 cm
According to the tangent-segment theorem, the length of the tangent (PT) from point P to the circle can be calculated using the formula:
PT=√OP2−r2
where:
- OP is the distance from point P to the center of the circle,
- r is the radius of the circle.
Substituting the known values into the formula:
PT=√(13)2−(5)2
Calculating the squares:
PT=√169−25
Now, perform the subtraction:
PT=√144
Finally, calculate the square root:
PT=12cm
Topper's Solved these Questions
- DIKSHA QUESTIONS Book:OSWAL PUBLICATIONChapter:DIKSHA QUESTIONS Exercise:Unit -IV: Geometry (Circles) (Very short Answer type questions)
Explore 6 Videos
- DIKSHA QUESTIONS Book:OSWAL PUBLICATIONChapter:DIKSHA QUESTIONS Exercise:Unit -IV: Geometry (Circles) (Short Answer type questions)
Explore 22 Videos
- DIKSHA QUESTIONS Book:OSWAL PUBLICATIONChapter:DIKSHA QUESTIONS Exercise:Unit -IV: Geometry (Triangles) (Long Answer Type Questions)
Explore 4 Videos
- COORDINATE GEOMETRYBook:OSWAL PUBLICATIONChapter:COORDINATE GEOMETRYExercise:SELF ASSESSMENT
Explore 20 Videos
- INTRODUCTION TO TRIGONOMETRY Book:OSWAL PUBLICATIONChapter:INTRODUCTION TO TRIGONOMETRY Exercise:Self - Assessment
Explore 15 Videos
Similar Questions
A point P is 13cm from the centre of the circle. The length of the tangent drawn from P to the circle is 12 cm. Find the radius of the circle.
View SolutionFrom a point P which is at a distance of 13 cm form the centre of the circle of radius 5 cm, a tangent is drawn to the circle . The length of the tangent is ____________
View Solution
Knowledge Check
A point P is 25 cm from the centre of the circle. The length of the tangent drawn from P to the circle is 24 cm. Find the radius of the circle.
A5 cmB7 cmC6 cmD8 cm
A point P is 25cm away from the centre of a circle and the lens of tangent drawn from P to the circle is 24cm. Find the radius.
View SolutionIf a point P is 17 cm from the centre of a circle of radius 8 cm, then find the length of the tangent drawn to the circle from point P.
View SolutionA point is 26 cm away from the centre O of a circle and the length PT of the tangent drawn from P to the circle is 10 cm. Find the radius of the circle.
View SolutionA point P is at a distance of 29cm from the centre of a circle of radius 20cm. Find the length of the tangent drawn from P to the circle.
View SolutionType I: A point P is 13cm from the center of the circle. The length of the tangent drawn from P to the circle is 12 cm . Find the radius of the circle ?
View Solution
A point P is 13 cm from the centre of the circle. The two tangent PQ and PR are drawn from the point P, The length of the tangent drawn from P to the circle is 12 cm.
Find the radius of the circle.
View Solution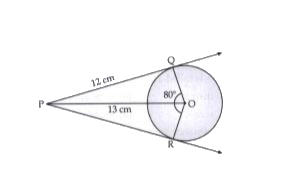
A point P is 13 cm from the centre of the circle. The two tangent PQ and PR are drawn from the point P, The length of the tangent drawn from P to the circle is 12 cm.
Find the length of OR.
View Solution

