In the measurement of the angle of a prism using a spectrometer, the readings of first reflected image are vernier I : , vernier II : and those of the second reflected image are vernier I : , vernier II : 24'. Then, the angle of the prism is
The correct Answer is:A
To find the angle of the prism using the given readings from a spectrometer, we can follow these steps:
1. Identify the Readings:
- For the first reflected image:
- Vernier I: 320∘40′
- Vernier II: 140∘30′
- For the second reflected image:
- Vernier I: 80∘38′
- Vernier II: 260∘24′
2. Calculate the Angles (φ1 and φ2):
- For φ1:
φ1=x2−x1
Where:
- x2=80∘38′ (from the second reflected image)
- x1=320∘40′ (from the first reflected image)
Performing the subtraction:
φ1=80∘38′−320∘40′
To perform this subtraction, we can convert the angles into minutes:
- 80∘38′=80×60+38=4820 minutes
- 320∘40′=320×60+40=19240 minutes
Now, subtract:
φ1=4820−19240=−14420 minutes
Since we are dealing with angles, we can add 360∘ (or 21600 minutes) to get a positive angle:
φ1=−14420+21600=7180 minutes=119∘58′
- For φ2:
φ2=y2−y1
Where:
- y2=260∘24′ (from the second reflected image)
- y1=140∘30′ (from the first reflected image)
Performing the subtraction:
φ2=260∘24′−140∘30′
Converting to minutes:
- 260∘24′=15624 minutes
- 140∘30′=8430 minutes
Now, subtract:
φ2=15624−8430=7194 minutes
Converting back to degrees:
φ2=119∘54′
3. Calculate the Total Angle (φ):
φ=φ1+φ2=119∘58′+119∘54′
Converting to minutes:
φ=(119×60+58)+(119×60+54)=7198+7174=14372 minutes
Converting back to degrees:
φ=239∘52′
4. Calculate the Angle of the Prism (A):
A=φ2=239∘52′2
Converting to minutes:
A=143722=7186 minutes
Converting back to degrees:
A=59∘58′
Final Answer:
The angle of the prism is 59∘58′.
---
- For the first reflected image:
- Vernier I: 320∘40′
- Vernier II: 140∘30′
- For the second reflected image:
- Vernier I: 80∘38′
- Vernier II: 260∘24′
- For φ1:
φ1=x2−x1
Where:
- x2=80∘38′ (from the second reflected image)
- x1=320∘40′ (from the first reflected image)
Performing the subtraction:
φ1=80∘38′−320∘40′
To perform this subtraction, we can convert the angles into minutes:
- 80∘38′=80×60+38=4820 minutes
- 320∘40′=320×60+40=19240 minutes
Now, subtract:
φ1=4820−19240=−14420 minutes
Since we are dealing with angles, we can add 360∘ (or 21600 minutes) to get a positive angle:
φ1=−14420+21600=7180 minutes=119∘58′
φ2=y2−y1
Where:
- y2=260∘24′ (from the second reflected image)
- y1=140∘30′ (from the first reflected image)
Performing the subtraction:
φ2=260∘24′−140∘30′
Converting to minutes:
- 260∘24′=15624 minutes
- 140∘30′=8430 minutes
Now, subtract:
φ2=15624−8430=7194 minutes
Converting back to degrees:
φ2=119∘54′
φ=φ1+φ2=119∘58′+119∘54′
Converting to minutes:
φ=(119×60+58)+(119×60+54)=7198+7174=14372 minutes
Converting back to degrees:
φ=239∘52′
A=φ2=239∘52′2
Converting to minutes:
A=143722=7186 minutes
Converting back to degrees:
A=59∘58′
The angle of the prism is 59∘58′.
Topper's Solved these Questions
- RAY OPTICSBook:DC PANDEY ENGLISHChapter:RAY OPTICSExercise:medical entrance special format question
Explore 23 Videos
- RAY OPTICSBook:DC PANDEY ENGLISHChapter:RAY OPTICSExercise:Medical entrance gallary
Explore 76 Videos
- RAY OPTICSBook:DC PANDEY ENGLISHChapter:RAY OPTICSExercise:Checkpoint 9.7
Explore 10 Videos
- NUCLEIBook:DC PANDEY ENGLISHChapter:NUCLEIExercise:C MADICAL ENTRANCES GALLERY
Explore 46 Videos
- REFLECTION OF LIGHTBook:DC PANDEY ENGLISHChapter:REFLECTION OF LIGHTExercise:Subjective
Explore 9 Videos
Similar Questions
A spectrometer gives the following reading when used to measure the angle of a prism.
Main scale reading : 58.5degree
Vernier scale reading : 09 divisions
Given that 1 division on main scale correspods to 0.5 degree. Total divisions on the vernier scale is 30 and match with 29 divisions of the main scale. the angle of the prism from the above data:
View SolutionA parallel beam of light falls normally on the first face of a prism of small angle .At the second face it is partly reflected,the reflected beam striking at the first face again, and emerging from it in a direction making an angle 6∘ 30' with the reversed direction of the incident beam. The refracted beam is found to have undergone a deviation of 1∘15' from the original direction.Find the refractive index of the glass and the angle of the prism.
View SolutionThe figure shows the path of a ray passing through an equiangular prism PQR. It is incident on face PR at angle slightly greater than the critical angle for total internal reflection . If the angle α shown in the figure is 30∘ . Calculate the R.I. of the material of the prism.
_E01_145_Q01.png)
View SolutionThe refractive indices of the crown glass for violet and red lights are1.51and 1.49respectively and those of the flint glass are1.77and1.73respectively A prism of angle 6∘is made of crown glass .A beam of white light is incident at a small angle on this prism.The other thin flint glass prism is combined white the crown glass prism such that te net mean deviation is1.5∘anticlockwise.
(i)Determine the angle of the flint glass prism.
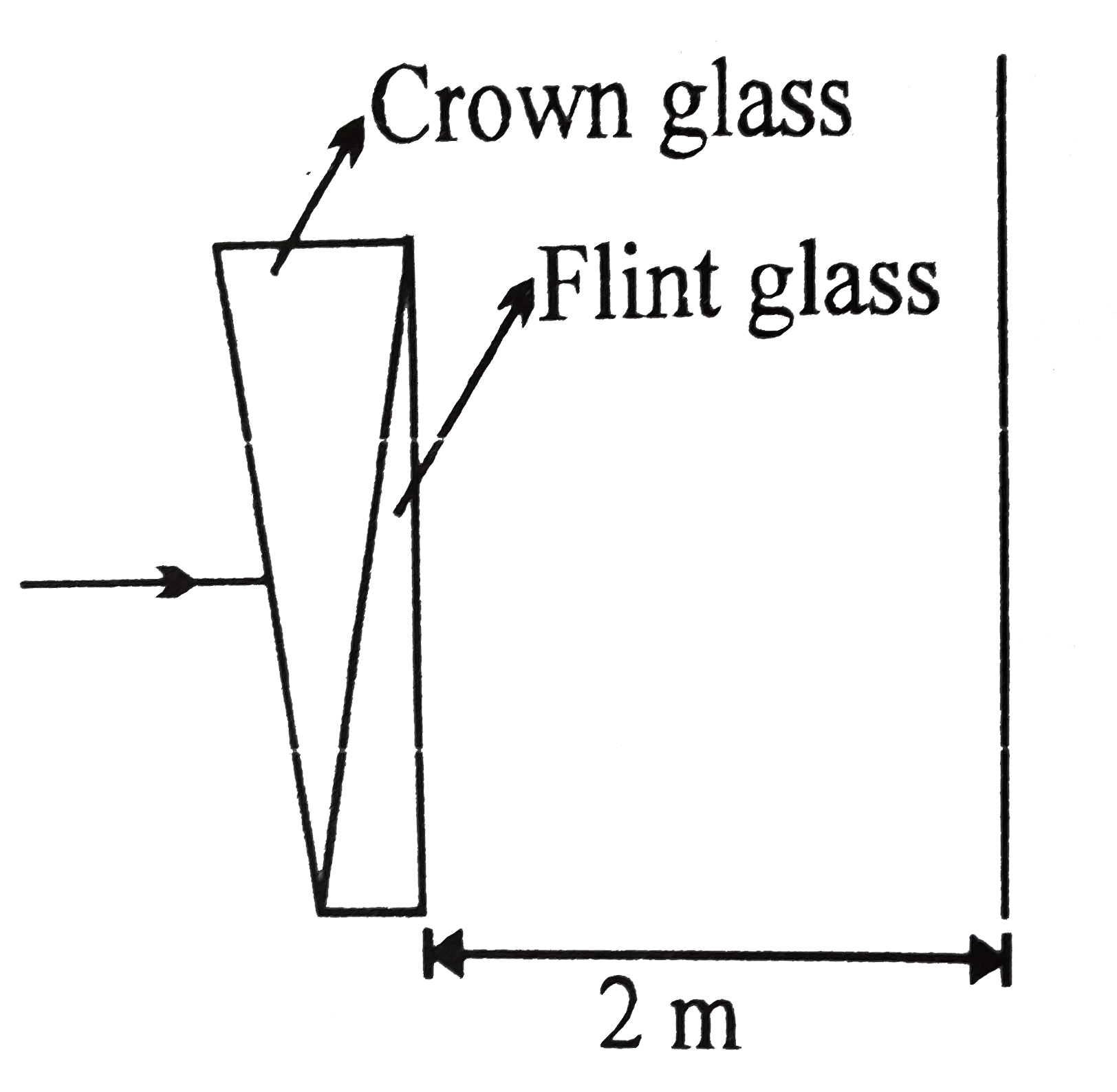
(ii)A screen is placed normal to the emerging beam at a distance of2mfrom the prism combination.find the distance between red and violet spot on the screen Which is the topmost colour on screen.
View SolutionA light ray of yellow colour is incident on an equilateral glass prism at an angle of incidence equal to 48∘ and suffers minimum deviation by an angle of 36∘. (i) What will be the angle of emergence ?
(ii) If the angle of incidence is changed to (a) 30∘
(b) 60∘, state in each case whether the angle of deviatioin will be equal to, less than or more than 36∘. ?
View SolutionFind the slope of a line i. which bisects the first quadrant angle ii. which makes an angle of 300 with the positive direction of y-axis measured anticlockwise.
View SolutionA ball is projected on a very long floor. There may be two conditions (i) floor is smooth &(ii) the collision is elastic
If both the considered then the path of ball is as follows.

Now if collision is inelastic and surface is rough then the path is as follows.

Successive range is decreasing .
Roughness of surface decreases the horizontal component of ball during collision and inelastic nature of collision decreases the vertical component of velocity of ball. In first case both components remain unchanged in magnitude and in second case both the components of the velocity will change.
Let us consider a third case here surface is rough but the collision of ball with floor is elastic. A ball is projected withe speed u at an angle 30∘ with horizontal and it is known that after collision with the floor its speed becomes u√3 . Then answer the following questions.
The angle made by the resultant velocity vector of the ball with horizontal after first collision with floor is :
View SolutionIn a Young's double slit experiment, a parallel beam containing wavelengths λ1=4000Å and λ2=5600Å is incident at an angle ϕ=30∘ on a diaphragm having narrow slits at separation d=2mm. The screen is placed at a distance D =40 cm from the slits. a mica slab of thickness t=5mm is placed in front of one of the slits and whole of the apparatus is submerged in water. if the central bright fringe is observed at C, determine.

(i) The refractive index of the slab
(ii) The distance of first black line from C
both wavelength are in air. take μw=43
View SolutionA ball is projected on a very long floor. There may be two conditions (i) floor is smooth &(ii) the collision is elastic
If both the considered then the path of ball is as follows.

Now if collision is inelastic and surface is rough then the path is as follows.

Successive range is decreasing .
Roughness of surface decreases the horizontal component of ball during collision and inelastic nature of collision decreases the vertical component of velocity of ball. In first case both components remain unchanged in magnitude and in second case both the components of the velocity will change.
Let us consider a third case here surface is rough but the collision of ball with floor is elastic. A ball is projected withe speed u at an angle 30∘ with horizontal and it is known that after collision with the floor its speed becomes u√3 . Then answer the following questions.
If the ball after first collision with the floor has rebounded vertically then the speed of the ball just after the collision with the floor would have been :
View SolutionA student performs an experiment to determine how the range of a ball depends on the velocity with which it is projected. The "range" is the distance between the points where the ball lends and from where it was projected, assuming it lands at the same height from which it was projected. It each trial, the student uses the same baseball, and launches it at the same angle. Table shows the experimental results.
∣∣ ∣ ∣ ∣ ∣ ∣∣TrailLaunch speed(m/s)Range(m)110822031.833070.7440122.5∣∣ ∣ ∣ ∣ ∣ ∣∣
Based on this data, the student then hypothesizes that the range, R, depends on the initial speed v0 according to the following equation : R=Cvn0, where C is a constant and n is another constant.
The student speculates that the constant C depends on :-
(i) The angle at which the ball was launched (ii) The ball's mass (iii) The ball's diameter
If we neglect air resistance, then C actually depends on :-
View Solution