A ray of light makes an angle of 10∘ with the horizontal and strikes a plane mirror which is inclined at an angle θ to the horizontal. The angle θ for which the reflected ray becomes vertical, is
40∘
50∘
80∘
100∘
The correct Answer is:A
To solve the problem, we need to find the angle θ at which the plane mirror must be inclined so that the reflected ray becomes vertical. Let's break down the solution step by step.
Step 1: Understand the given angles
The ray of light makes an angle of 10∘ with the horizontal. This means that the angle of incidence i with respect to the normal to the mirror is:
i=90∘−10∘=80∘
Hint: Remember that the angle of incidence is measured from the normal, not the horizontal.
Step 2: Relate the angle of incidence and reflection
According to the law of reflection, the angle of incidence is equal to the angle of reflection. Therefore, the angle of reflection r is:
r=i=80∘
Hint: The law of reflection states that the angle of incidence equals the angle of reflection.
Step 3: Determine the angle of the reflected ray with respect to the mirror
The angle between the reflected ray and the plane of the mirror is given by:
Angle with mirror=90∘−r=90∘−80∘=10∘
Hint: The angle with the mirror is complementary to the angle of reflection.
Step 4: Find the angle of the reflected ray with respect to the horizontal
Since the mirror is inclined at an angle θ to the horizontal, the angle of the reflected ray with respect to the horizontal will be:
Angle with horizontal=θ+10∘
Hint: When adding angles, ensure you account for the inclination of the mirror.
Step 5: Set the angle of the reflected ray to be vertical
For the reflected ray to be vertical, its angle with the horizontal must be 90∘. Therefore, we set up the equation:
θ+10∘=90∘
Hint: A vertical ray has an angle of 90∘ with the horizontal.
Step 6: Solve for θ
Now, we can solve for θ:
θ=90∘−10∘=80∘
Final Answer
Thus, the angle θ for which the reflected ray becomes vertical is:
θ=80∘
---
The ray of light makes an angle of 10∘ with the horizontal. This means that the angle of incidence i with respect to the normal to the mirror is:
i=90∘−10∘=80∘
According to the law of reflection, the angle of incidence is equal to the angle of reflection. Therefore, the angle of reflection r is:
r=i=80∘
The angle between the reflected ray and the plane of the mirror is given by:
Angle with mirror=90∘−r=90∘−80∘=10∘
Since the mirror is inclined at an angle θ to the horizontal, the angle of the reflected ray with respect to the horizontal will be:
Angle with horizontal=θ+10∘
For the reflected ray to be vertical, its angle with the horizontal must be 90∘. Therefore, we set up the equation:
θ+10∘=90∘
Now, we can solve for θ:
θ=90∘−10∘=80∘
Thus, the angle θ for which the reflected ray becomes vertical is:
θ=80∘
Topper's Solved these Questions
- RAY OPTICSBook:DC PANDEY ENGLISHChapter:RAY OPTICSExercise:medical entrance special format question
Explore 23 Videos
- RAY OPTICSBook:DC PANDEY ENGLISHChapter:RAY OPTICSExercise:Medical entrance gallary
Explore 76 Videos
- RAY OPTICSBook:DC PANDEY ENGLISHChapter:RAY OPTICSExercise:Checkpoint 9.7
Explore 10 Videos
- NUCLEIBook:DC PANDEY ENGLISHChapter:NUCLEIExercise:C MADICAL ENTRANCES GALLERY
Explore 46 Videos
- REFLECTION OF LIGHTBook:DC PANDEY ENGLISHChapter:REFLECTION OF LIGHTExercise:Subjective
Explore 9 Videos
Similar Questions
A ray of light is incident at an angle of 30∘ with the plane of a plane mirror. Find the angle of reflection.
View SolutionA light ray strikes a horizontal plane mirror and gets deviated by π/3. By what angle should the mirror be tilted so that the reflected ray becomes vertical?
View SolutionA mirror is inclined at an angle of θ with the horizontal. If a ray light is incident at an angle θ as shown , then the angle made by reflected ray with the horizontal is
_E01_002_Q01.png)
View SolutionA ray of light is incident at an ∠ of 30∘ on a plane mirror M1. Another mirror M2 is inclined at angle θ to M1. What is the value of angle θ so light reflected from M2 is parallel to M1.
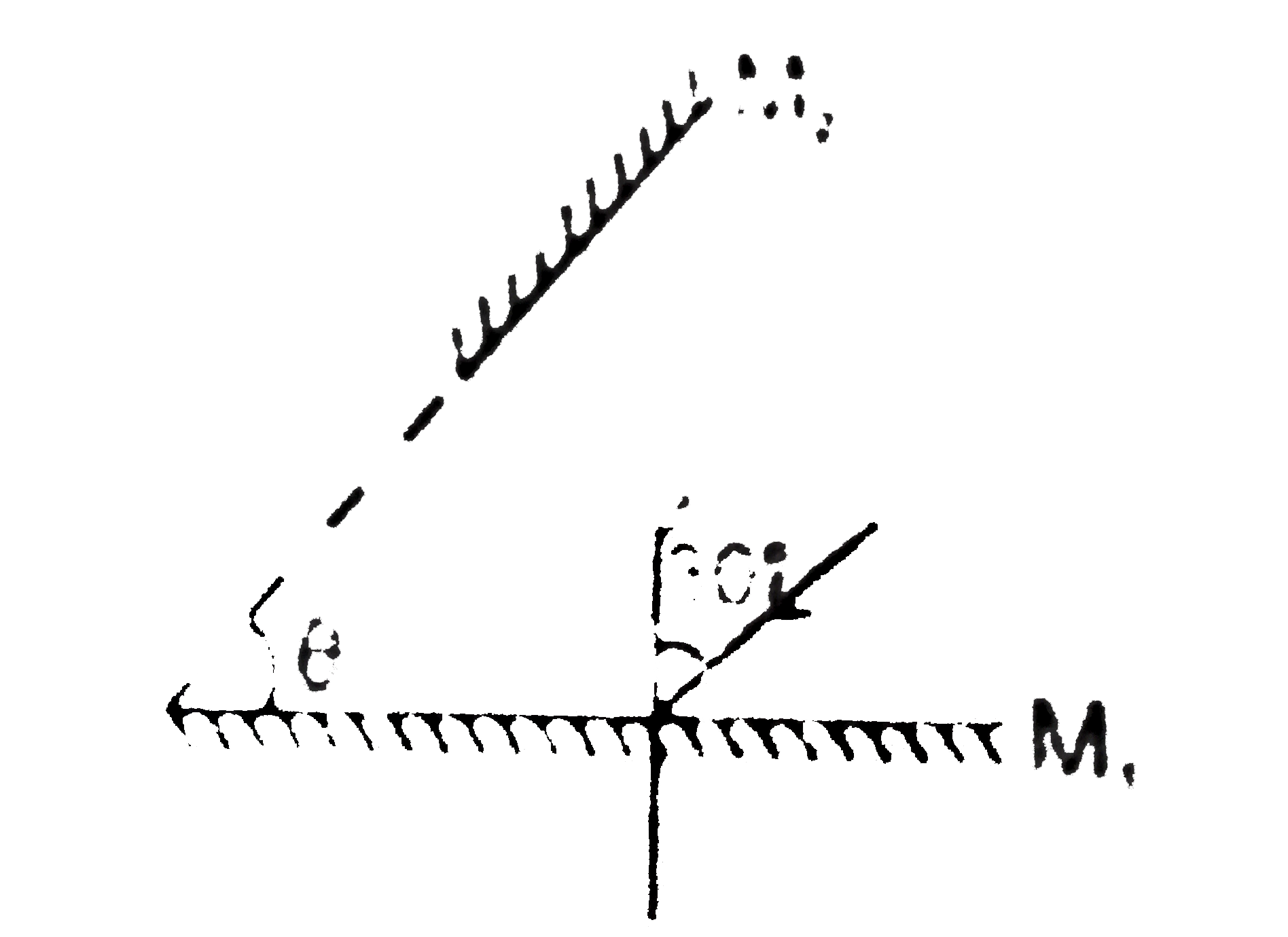 .
.
View SolutionA particle is thrown at time t = 0 with a velocity of 10ms−1 at an angle 60∘ with the horizontal from a point on an inclined plane, making an angle of 30∘ with the horizontal. The time when the velocity of the projectile becomes parallel to the incline is

View SolutionA particle is thrown at time t = 0 with a velocity of 10ms−1 at an angle 60∘ with the horizontal from a point on an inclined plane, making an angle of 30∘ with the horizontal. The time when the velocity of the projectile becomes parallel to the incline is

View SolutionA particle is thrown at time t = 0 with a velocity of 10ms−1 at an angle 60∘ with the horizontal from a point on an inclined plane, making an angle of 30∘ with the horizontal. The time when the velocity of the projectile becomes parallel to the incline is

View SolutionA projectile is fired with a velocity v at right angle to the slope inclined at an angle θ with the horizontal. The range of the projectile along the inclined plane is

View SolutionA plane mirrorr makes an angle of 30∘ with horizontal. If a vertical ray strikes mirrorr, find the angle between mirrorr and reflected ray
View SolutionWhen a plane mirror is rotated through an angle θ then the reflected ray turns through the angle 2θ then the size of the image
View Solution

