Question

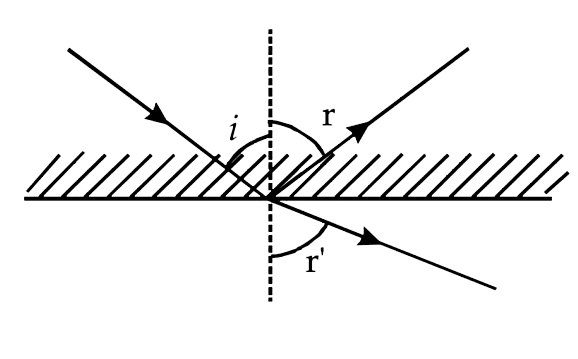
If a ray of light in a denser medium strikes a rarer medium at an angle of incidence i, the angles of reflection and refraction are respectively, r and r' If the reflected and refraction rays are at right angles to each other, the critical angle for the given pair of media is

Options

A. `sin^(-1)(tanr')`
B. `sin^(-1)(tanr)`
C. `tan^(-1)(sini)`
D. `cot^(-1)(tani)`

Answer

B

Explanation

To solve the problem, we need to find the critical angle (θc) for a ray of light transitioning from a denser medium to a rarer medium, given that the reflected and refracted rays are at right angles to each other.

1. Understanding the Situation:
- We have a ray of light moving from a denser medium (n1) to a rarer medium (n2).
- The angle of incidence is denoted as \(i\), the angle of reflection as \(r\), and the angle of refraction as \(r'\).
- According to the problem, the reflected ray and the refracted ray are at right angles to each other, meaning \(r + r' = 90^\circ\).

2. Using Snell's Law:
- Snell's Law states that:
\( n_1 \sin(i) = n_2 \sin(r') \)
- Since we are moving from a denser medium (n1) to a rarer medium (n2), we can express \(n_2\) in terms of \(n_1\):
\( n_2 = \frac{n_1}{n} \)
- Rearranging gives us:
\( \sin(i) = \frac{n_2}{n_1} \sin(r') \)

3. Relating Angles:
- Since \(r' = 90^\circ - r\), we can substitute this into our equation:
\( \sin(i) = \frac{n_2}{n_1} \sin(90^\circ - r) = \frac{n_2}{n_1} \cos(r) \)

4. Expressing n2 in terms of n1:
- From Snell's Law, we can express \(n_2\) as:
\( n_2 = n_1 \sin(i) / \cos(r) \)
- This can be simplified to:
\( n_2 = n_1 \tan(i) \)

5. Finding the Critical Angle:
- The critical angle \(θ_c\) occurs when \(r' = 90^\circ\). Thus:
\( n_1 \sin(θ_c) = n_2 \)
- Substituting \(n_2\) gives:
\( n_1 \sin(θ_c) = n_1 \tan(i) \)
- Dividing both sides by \(n_1\) (assuming \(n_1 \neq 0\)):
\( \sin(θ_c) = \tan(i) \)

6. Final Expression for Critical Angle:
- The critical angle can be expressed as:
\( θ_c = \sin^{-1}(\tan(i)) \)

Conclusion:
Thus, the critical angle for the given pair of media is:
\( θ_c = \sin^{-1}(\tan(i)) \)