An object is placed at 21 cm in front of a concave mirror of radius of a curvature 10 cm. A glass slab of thickness 3 cm and u 15 is then placed close to the mirror in the space between the object and the mirror. The position of final image formed is
−3.94cm
4.3 cm
−4.93
3.94 cm
The correct Answer is:C
To solve the problem step-by-step, we will follow the outlined approach to find the position of the final image formed by the concave mirror after placing the glass slab.
Step 1: Determine the focal length of the concave mirror
The radius of curvature (R) of the concave mirror is given as 10 cm. The focal length (f) is related to the radius of curvature by the formula:
f=R2
Substituting the value of R:
f=10cm2=5cm
Step 2: Calculate the increase in path due to the glass slab
The thickness (T) of the glass slab is given as 3 cm, and the refractive index (μ) is 1.5. The increase in path length (Δ) due to the glass slab is calculated using the formula:
Δ=(μ−1)⋅T
Substituting the values:
Δ=(1.5−1)⋅3cm=0.5⋅3cm=1.5cm
Step 3: Calculate the new object distance (u')
The object is initially placed at 21 cm in front of the mirror. However, due to the glass slab, the effective object distance (u') will be modified by the increase in path length:
u′=−(21cm+1.5cm)=−22.5cm
Step 4: Apply the mirror formula to find the image distance (v)
The mirror formula is given by:
1f=1u′+1v
Rearranging the formula to find v:
1v=1f−1u′
Substituting the known values (f = 5 cm and u' = -22.5 cm):
1v=15−1−22.5
Calculating the right side:
1v=15+122.5
Finding a common denominator (which is 22.5 * 5 = 112.5):
1v=22.5+5112.5=27.5112.5
Calculating v:
v=112.527.5≈4.09cm
Step 5: Calculate the geometrical distance
Since the image distance is positive, it indicates that the image is formed on the same side as the object. However, we need to account for the thickness of the glass slab when determining the final geometrical distance from the mirror:
Geometrical distance=v−Δ=4.09cm−1.5cm=2.59cm
Final Answer
The position of the final image formed is approximately 2.59 cm in front of the mirror.
---
The radius of curvature (R) of the concave mirror is given as 10 cm. The focal length (f) is related to the radius of curvature by the formula:
The thickness (T) of the glass slab is given as 3 cm, and the refractive index (μ) is 1.5. The increase in path length (Δ) due to the glass slab is calculated using the formula:
The object is initially placed at 21 cm in front of the mirror. However, due to the glass slab, the effective object distance (u') will be modified by the increase in path length:
The mirror formula is given by:
Since the image distance is positive, it indicates that the image is formed on the same side as the object. However, we need to account for the thickness of the glass slab when determining the final geometrical distance from the mirror:
The position of the final image formed is approximately 2.59 cm in front of the mirror.
Topper's Solved these Questions
- RAY OPTICSBook:DC PANDEY ENGLISHChapter:RAY OPTICSExercise:medical entrance special format question
Explore 23 Videos
- RAY OPTICSBook:DC PANDEY ENGLISHChapter:RAY OPTICSExercise:Medical entrance gallary
Explore 76 Videos
- RAY OPTICSBook:DC PANDEY ENGLISHChapter:RAY OPTICSExercise:Checkpoint 9.7
Explore 10 Videos
- NUCLEIBook:DC PANDEY ENGLISHChapter:NUCLEIExercise:C MADICAL ENTRANCES GALLERY
Explore 46 Videos
- REFLECTION OF LIGHTBook:DC PANDEY ENGLISHChapter:REFLECTION OF LIGHTExercise:Subjective
Explore 9 Videos
Similar Questions
An object is placed 21 cm in front of a concave mirror of radius of curvature 10cm. A glass slabe of thickness 3cm and refractive index 1.5 is then placed close to the irror in the space between the object and the mirror. The distance of the near surface of the slabe from the mirror is 1cm. The final image from the mirror will be formed at
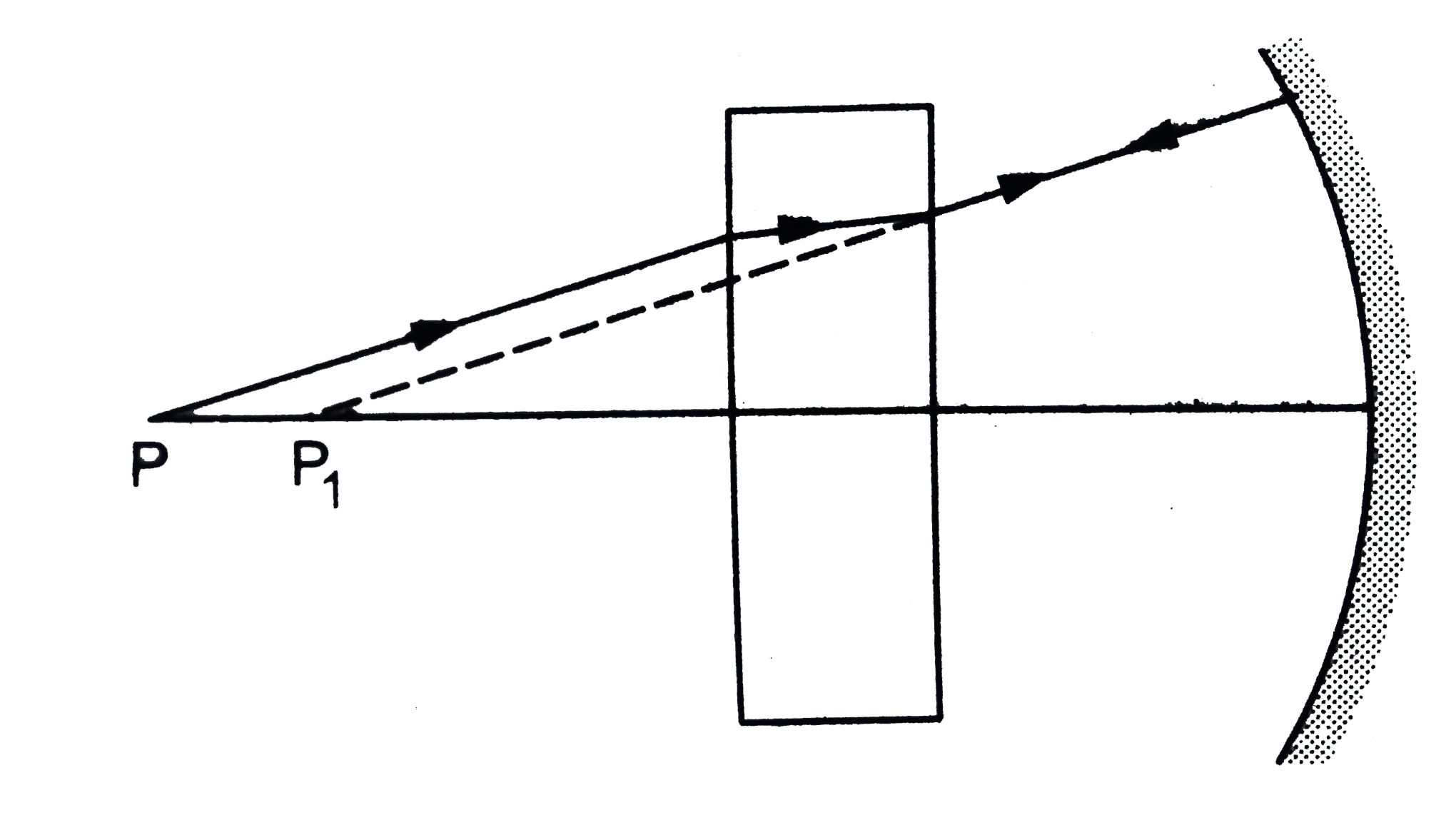
View SolutionAn object is placed 21 cm in fron of a concave mirror of radius of curvature 20 cm.A glass slab of thicknes 3 cm and refractive index 1.5 is palced close to the mirror in the space between the object and the mirror. Find the position of the final image fromed. The distance of the nearer surface of the slab from the mirror is 10 cm.
View SolutionAn object is placed at 4 cm distance in front of a concave mirror of radius of curvature 24 cm. Find the position of image. Is the image magnified?
View SolutionAn object 2.5 cm high is placed at a distance of 10 cm from a concave mirror of radius of curvature 30 cm The size of the image is
View SolutionA point object is placed 33cm from a convex mirror of curvature radius =40cm A glass plate of thickness 6cm and refractive index 2.0 placed between the object and mirror,close to the mirror,find the distance of final image form the object?
View SolutionAn object of size 7.5 cm is placed in front of a convex mirror of radius of curvature 25 cm at a distance of 40 cm. The size of the image should be
View SolutionA point object O is placed in front of a concave mirror of focal length 10cm. A glass slab of refractive index μ=3/2 and thickness 6cm is inserted between the object and mirror.
Find the position of final image when the distance x shown in Fig... is, (a) 5cm and (b) 20 cm.
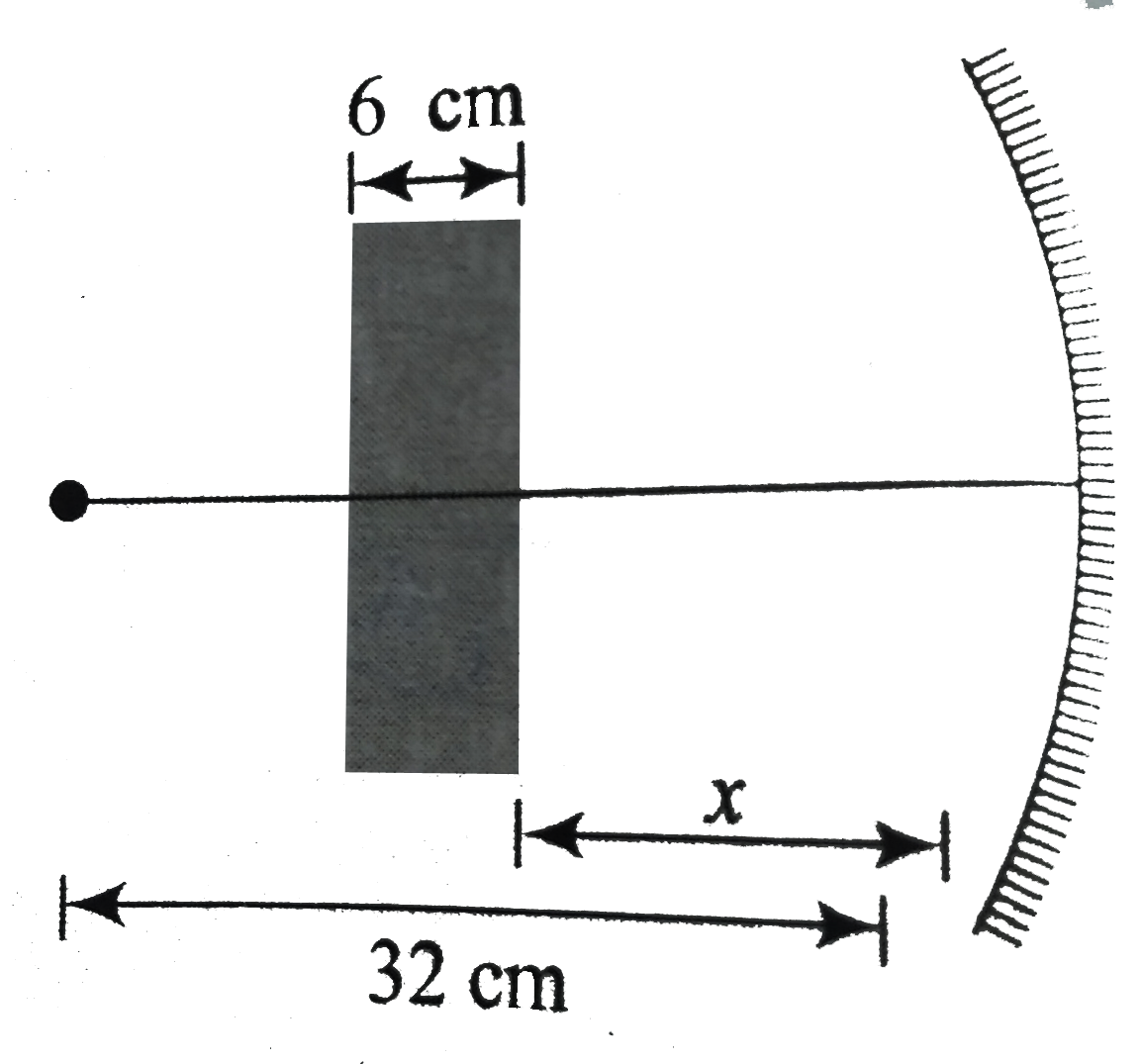
View SolutionA point object O is placed in front of a concave mirror of focal length 10cm. A glass slab of refractive index μ=3/2 and thickness 6cm is inserted between the object and mirror.

Q. Find the position and nature of the final image when the distance x shown in figure, is 5cm.
View SolutionA linear object of heigth 10 cm is kept in front of concave mirror of radius of curvature 15 cm, at distance of 10 cm. The image formed is
View SolutionAn object is placed at 6 cm distance in front of a concave mirror of focal length 4 cm.
Find the position of the image period.
View Solution