A point object is placed 33cm from a convex mirror of curvature radius =40cm A glass plate of thickness 6cm and refractive index 2.0 placed between the object and mirror,close to the mirror,find the distance of final image form the object?
The correct Answer is:sin−1(1)√3
To solve the problem step by step, we will follow the outlined procedure:
Step 1: Determine the Shift Due to the Glass Plate
The shift caused by the glass plate can be calculated using the formula:
Shift=Thickness×(1−1Refractive Index)
Given:
- Thickness of the glass plate = 6cm
- Refractive index of the glass plate = 2.0
Calculating the shift:
Shift=6×(1−12)=6×(1−0.5)=6×0.5=3cm
Step 2: Adjust the Object Distance
The object distance U is given as 33cm. Since the shift is in the direction of light travel, we subtract the shift from the object distance:
U=−(33−3)=−30cm
Step 3: Calculate the Focal Length of the Convex Mirror
The focal length F of a convex mirror is given by:
F=R2
where R is the radius of curvature.
Given:
- Radius of curvature R=40cm
Calculating the focal length:
F=402=20cm
Step 4: Use the Mirror Formula to Find the Image Distance
The mirror formula is given by:
1F=1V+1U
Rearranging gives:
1V=1F−1U
Substituting the values:
1V=120−1−30
Calculating the right side:
1V=120+130
Finding a common denominator (60):
1V=360+260=560=112
Thus,
V=12cm
Step 5: Adjust the Image Distance for the Shift
Since the shift is in the direction of light travel, we need to adjust the image distance:
V′=V−Shift=12−3=9cm
Step 6: Calculate the Distance Between the Object and the Image
The distance between the object and the image is given by:
Distance=|U|+|V′|=33+9=42cm
Final Answer
The distance of the final image from the object is 42cm.
---
The shift caused by the glass plate can be calculated using the formula:
Shift=Thickness×(1−1Refractive Index)
- Thickness of the glass plate = 6cm
- Refractive index of the glass plate = 2.0
Shift=6×(1−12)=6×(1−0.5)=6×0.5=3cm
The object distance U is given as 33cm. Since the shift is in the direction of light travel, we subtract the shift from the object distance:
U=−(33−3)=−30cm
The focal length F of a convex mirror is given by:
F=R2
where R is the radius of curvature.
- Radius of curvature R=40cm
F=402=20cm
The mirror formula is given by:
1F=1V+1U
Rearranging gives:
1V=1F−1U
1V=120−1−30
Calculating the right side:
1V=120+130
Finding a common denominator (60):
1V=360+260=560=112
Thus,
V=12cm
Since the shift is in the direction of light travel, we need to adjust the image distance:
V′=V−Shift=12−3=9cm
The distance between the object and the image is given by:
Distance=|U|+|V′|=33+9=42cm
The distance of the final image from the object is 42cm.
Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE-04[B]
18 Videos
- GEOMETRICAL OPTICSBOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE-05 (A)
35 Videos
- GEOMETRICAL OPTICSBOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE-3
12 Videos
- CURRENT ELECTRICITYBOOK - ALLENCHAPTER - CURRENT ELECTRICITYEXERCISE - EX.II
66 Videos
- GRAVITATIONBOOK - ALLENCHAPTER - GRAVITATIONEXERCISE - EXERCISE 4
9 Videos
Similar Questions
An object is placed 21 cm in front of a concave mirror of radius of curvature 10cm. A glass slabe of thickness 3cm and refractive index 1.5 is then placed close to the irror in the space between the object and the mirror. The distance of the near surface of the slabe from the mirror is 1cm. The final image from the mirror will be formed at
View SolutionAn object is placed 21 cm in fron of a concave mirror of radius of curvature 20 cm.A glass slab of thicknes 3 cm and refractive index 1.5 is palced close to the mirror in the space between the object and the mirror. Find the position of the final image fromed. The distance of the nearer surface of the slab from the mirror is 10 cm.
View SolutionAn object is placed at 21 cm in front of a concave mirror of radius of a curvature 10 cm. A glass slab of thickness 3 cm and u 15 is then placed close to the mirror in the space between the object and the mirror. The position of final image formed is
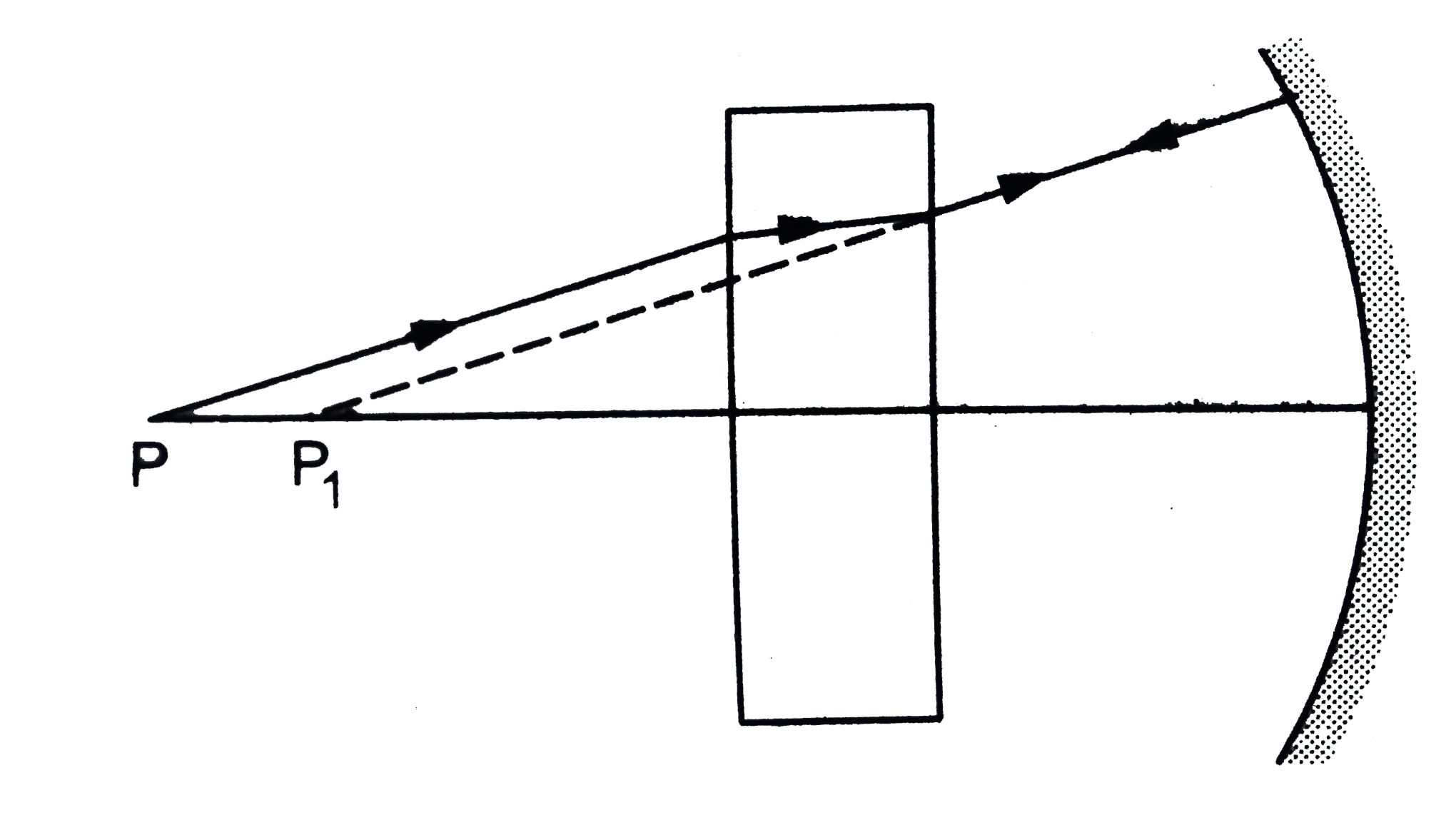
View SolutionA point object is placed on principal axis of a concave mirror of radius of curvature 20cm at a distance 31cm from poll of the mirror. A glass slab of thikness 3cm and refractive index 1.5 is placed between object and mirror as shown in the figure. Find the distance (in cm) of final image formed by the system from the mirror.
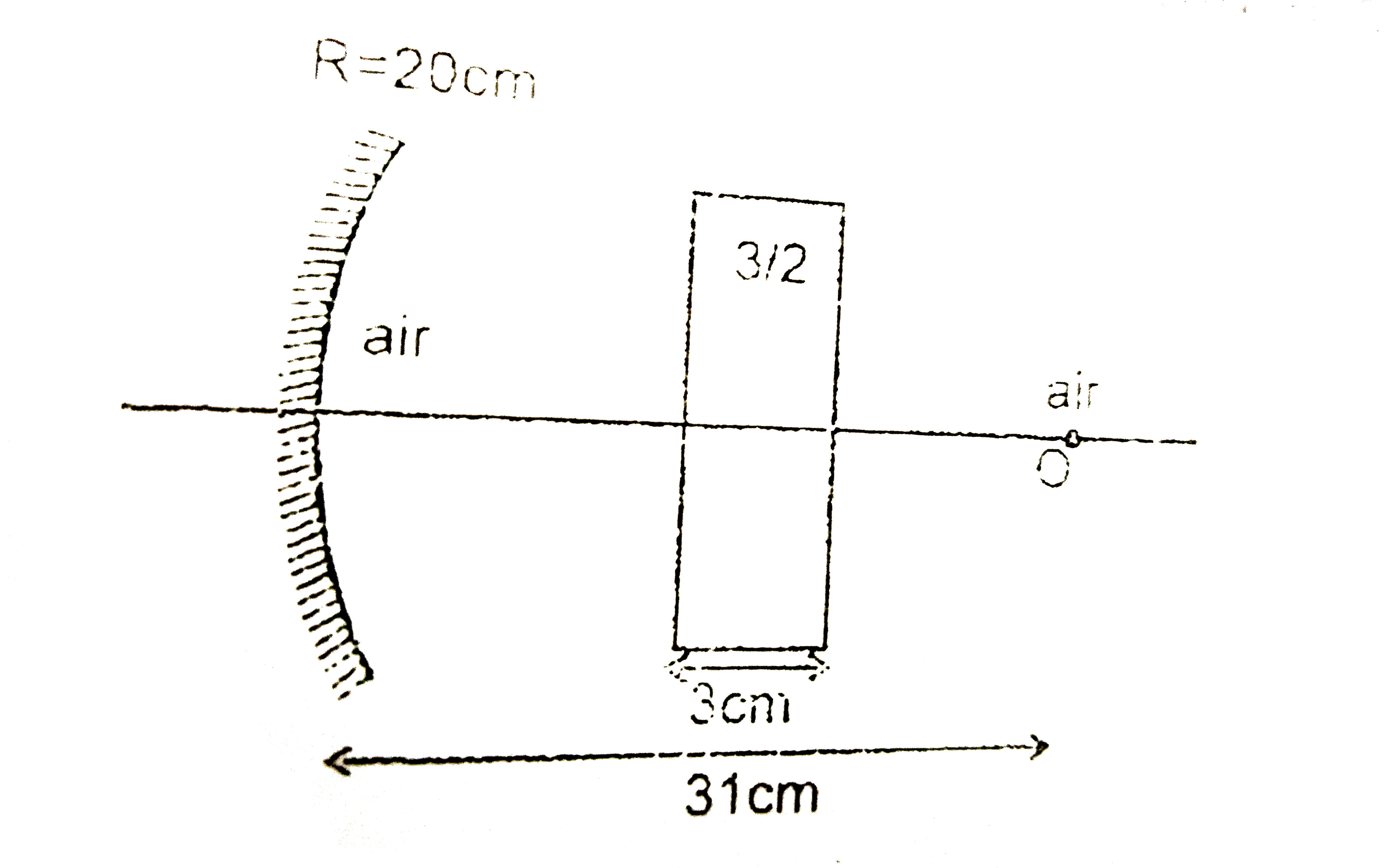
View SolutionA point object O is placed in front of a concave mirror of focal length 10cm. A glass slab of refractive index μ=3/2 and thickness 6cm is inserted between the object and mirror.

Q. Find the position and nature of the final image when the distance x shown in figure, is 5cm.
View SolutionAn object is placed 40 cm from a concave mirror of focal length 20 cm. The image formed is
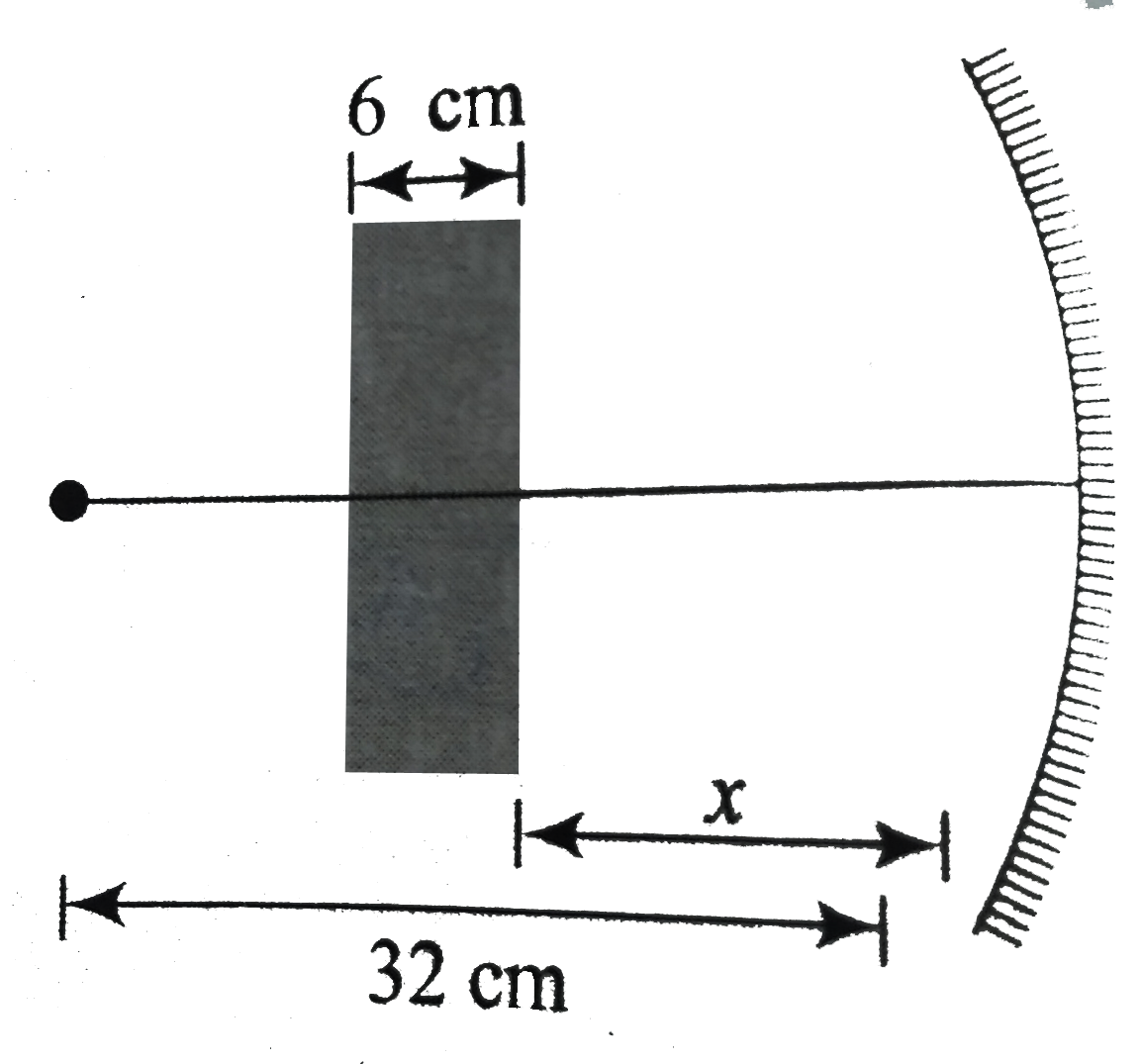
View SolutionA point object O is placed in front of a concave mirror of focal length 10cm. A glass slab of refractive index μ=3/2 and thickness 6cm is inserted between the object and mirror.
Find the position of final image when the distance x shown in Fig... is, (a) 5cm and (b) 20 cm.
View SolutionAn object is placed at 20 cm from a convex mirror of focal length 10 cm. The image formed by a mirror is
View SolutionA glass slab of thickness 3cm and refractive index 1.5 is placed in front of a concave mirror of focal length 20cm. Where should a point object be placed if it is to image on to itself?
View SolutionAn object is placed on the principle axis of a concave mirror of focal length 10cm at a distance of 21cm from it. A glass slab is placed between the mirror and the object as shown in figure.
Find the distance of final image formed by the mirror.

View Solution
