Light from a luminious point on the lower face of a rectangular glass slab , 2 cm thick, strikes the upper face and the totally reflected rays outline a circle of 3.2 cm radius on the lower face. Find the refractive index of the glass.
The correct Answer is:1.17
To solve the problem, we need to find the refractive index of the glass slab given the thickness of the slab and the radius of the circle outlined by the totally reflected rays on the lower face.
1. Understand the Geometry:
- We have a rectangular glass slab with a thickness (t) of 2 cm.
- A luminous point is located on the lower face of the slab.
- The rays of light strike the upper face and undergo total internal reflection, outlining a circle of radius (r) = 3.2 cm on the lower face.
2. Identify the Angles:
- Let’s denote the angle of incidence at the upper face as C.
- The angle of refraction at the upper face is 90∘ since the rays are totally internally reflected.
3. Apply Snell's Law:
- According to Snell's Law:
μ1sinC=μ2sin90∘
- Here, μ2 (the refractive index of air) is 1, and sin90∘=1.
- Therefore, we can simplify this to:
μ1sinC=1
- Rearranging gives:
μ1=1sinC
4. Determine the Geometry of the Circle:
- The radius of the circle (r) formed on the lower face is 3.2 cm.
- The distance from the luminous point to the upper face is the thickness of the slab (t = 2 cm).
- We can visualize a right triangle where:
- The opposite side is the radius (r = 3.2 cm).
- The adjacent side is the thickness of the slab (t = 2 cm).
- Using the Pythagorean theorem, we can find the hypotenuse (h):
h=√r2+t2=√(3.2)2+(2)2
h=√10.24+4=√14.24≈3.77 cm
5. Calculate sinC:
- From the triangle, we can find sinC:
sinC=oppositehypotenuse=rh=3.23.77≈0.847
6. Find the Refractive Index:
- Now, substituting sinC back into the equation for μ1:
μ1=1sinC=10.847≈1.18
Final Answer:
The refractive index of the glass slab is approximately 1.18.
- We have a rectangular glass slab with a thickness (t) of 2 cm.
- A luminous point is located on the lower face of the slab.
- The rays of light strike the upper face and undergo total internal reflection, outlining a circle of radius (r) = 3.2 cm on the lower face.
- Let’s denote the angle of incidence at the upper face as C.
- The angle of refraction at the upper face is 90∘ since the rays are totally internally reflected.
- According to Snell's Law:
μ1sinC=μ2sin90∘
- Here, μ2 (the refractive index of air) is 1, and sin90∘=1.
- Therefore, we can simplify this to:
μ1sinC=1
- Rearranging gives:
μ1=1sinC
- The radius of the circle (r) formed on the lower face is 3.2 cm.
- The distance from the luminous point to the upper face is the thickness of the slab (t = 2 cm).
- We can visualize a right triangle where:
- The opposite side is the radius (r = 3.2 cm).
- The adjacent side is the thickness of the slab (t = 2 cm).
- Using the Pythagorean theorem, we can find the hypotenuse (h):
h=√r2+t2=√(3.2)2+(2)2
h=√10.24+4=√14.24≈3.77 cm
- From the triangle, we can find sinC:
sinC=oppositehypotenuse=rh=3.23.77≈0.847
- Now, substituting sinC back into the equation for μ1:
μ1=1sinC=10.847≈1.18
The refractive index of the glass slab is approximately 1.18.
Topper's Solved these Questions
- GEOMETRICAL OPTICSBook:ALLENChapter:GEOMETRICAL OPTICSExercise:EXERCISE-04[B]
Explore 18 Videos
- GEOMETRICAL OPTICSBook:ALLENChapter:GEOMETRICAL OPTICSExercise:EXERCISE-05 (A)
Explore 35 Videos
- GEOMETRICAL OPTICSBook:ALLENChapter:GEOMETRICAL OPTICSExercise:EXERCISE-3
Explore 12 Videos
- CURRENT ELECTRICITYBook:ALLENChapter:CURRENT ELECTRICITYExercise:EX.II
Explore 66 Videos
- GRAVITATIONBook:ALLENChapter:GRAVITATIONExercise:EXERCISE 4
Explore 9 Videos
Similar Questions
Onc face of a rectangular glass plate 6 cm thick is silcerd. An object held 8 cm in front of the first face, froms an image 12 cm behind the silvered face. The refractive index of the glass is
View SolutionOne face of a rectangular glass plate 6 cm thick is silvered. An object held 8 cm in front of the first face, forms an image 12 cm behind the silvered face. The refractive index of the glass is
View SolutionOne face of a rectangular glass plate 6 cm thick is silvered. An object held 8 cm in front of the first face, forms an image 12 cm behind the silvered face. The refractive index of the glass is
View SolutionOne face of a rectangular glass plate 6cm thick is silvered. An object held 8cm in front of the unsilvered face forms an image 10cm behind the silvered face.Find the refractive index of glass. Consider all the three steps.
View SolutionA narrow beam of monochromatic light, PQ, is incident normally on one face of an equiangular glass prism of refractive index 1.45. When the prism is immersed in a certain liquid, the ray makes a grazing emergence along the other face (figure). Find the refractive index of this liquid .
View SolutionA small object is placed 20 cm in front of a block of glass 10 cm thick and its farther side silvered. The image is formed 22 cm behind the silvered face. Find the refractive index of glass.
View SolutionA narrow beam of monochromatic light, pe, is incident normally on one face of an equiangular glass prism of refractive inder 1-45. When the prism is immersed in a certain liquid, the ray makes a grazing emergence along the other face (See below figure). Find the refractive index of this liquid.

View SolutionA light ray falls on a rectangular glass slab as shown. The index of refraction of the glass, if total internal reflection is to occur at the vertical face, is

View SolutionA ray of light is incident on one face of a transparent glass slab of thickness 9cm at an angle of incidence 60∘. Lateral displacement of the ray on emerging from the opposite parallel face is 3√3cm. Refractive index of the material of slab is:
View SolutionAn object O is placed at 8cm in front of a glass slab, whose one face is silvered as shown in Figure. The thickness of the slab is 6cm. If the image formed 10 cm behind the silvered face, find the refractive index of glass.
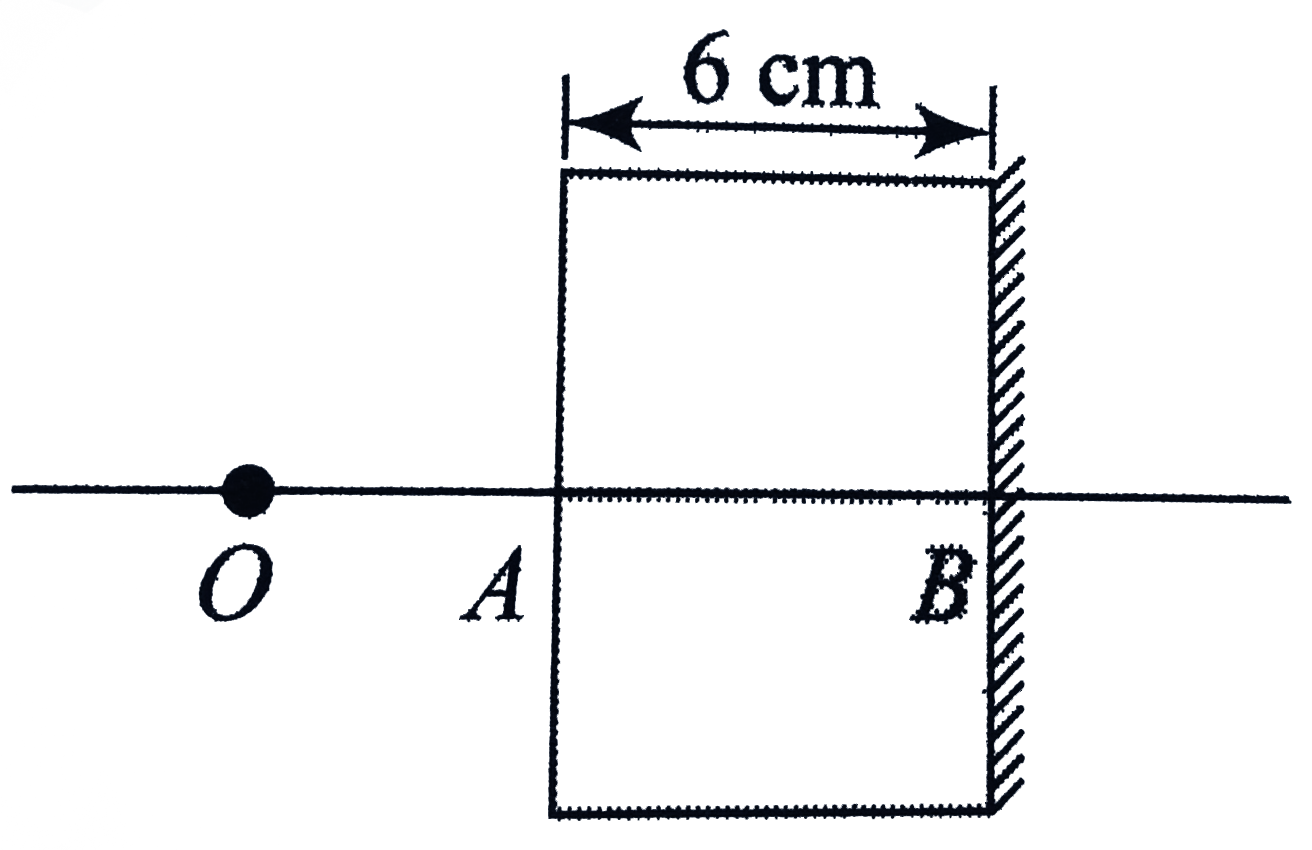
View Solution

