A circular beam of light (diameter d) falls on a plane surface of a liquid. The angle of incidence is and refractive index of the liquid is . The diameter of the refracted beam is
d
The correct Answer is:C
To solve the problem of finding the diameter of the refracted beam when a circular beam of light with diameter d falls on a plane surface of a liquid at an angle of incidence of 45∘, we can follow these steps:
Step 1: Understand the Geometry
We have a circular beam of light with diameter d incident on the surface of a liquid. The angle of incidence I is given as 45∘. The refractive index of the liquid is μ.
Step 2: Apply Snell's Law
Using Snell's Law at the interface of air and liquid:
μairsinI=μliquidsinR
Since μair=1 and I=45∘, we have:
sin45∘=μsinR
This simplifies to:
1√2=μsinR
Thus,
sinR=1μ√2
Step 3: Calculate cosR
Using the identity cos2R+sin2R=1:
cos2R=1−sin2R=1−(1μ√2)2
This gives:
cosR=√1−12μ2=√2μ2−12μ2
Step 4: Relate the Diameters Before and After Refraction
From the geometry of the situation, we can relate the diameters before and after refraction using the triangles formed:
1. For the incident beam:
AC=dcosI=dcos45∘=d1√2=d√2
2. For the refracted beam:
AC=D′cosR
Setting these equal gives:
d√2=D′cosR
Thus,
D′=d√2cosR
Step 5: Substitute cosR
Substituting the expression for cosR:
D′=d√2⋅√2μ2−12μ2=d⋅√2⋅√2μ2−1μ
Step 6: Final Expression for Diameter of Refracted Beam
Thus, the diameter of the refracted beam D′ is:
D′=d√2(2μ2−1)μ
Final Answer
The diameter of the refracted beam is:
D′=dμ√2μ2−1
We have a circular beam of light with diameter d incident on the surface of a liquid. The angle of incidence I is given as 45∘. The refractive index of the liquid is μ.
Using Snell's Law at the interface of air and liquid:
μairsinI=μliquidsinR
Since μair=1 and I=45∘, we have:
sin45∘=μsinR
This simplifies to:
1√2=μsinR
Thus,
sinR=1μ√2
Using the identity cos2R+sin2R=1:
cos2R=1−sin2R=1−(1μ√2)2
This gives:
cosR=√1−12μ2=√2μ2−12μ2
From the geometry of the situation, we can relate the diameters before and after refraction using the triangles formed:
1. For the incident beam:
AC=dcosI=dcos45∘=d1√2=d√2
2. For the refracted beam:
AC=D′cosR
d√2=D′cosR
Thus,
D′=d√2cosR
Substituting the expression for cosR:
D′=d√2⋅√2μ2−12μ2=d⋅√2⋅√2μ2−1μ
Thus, the diameter of the refracted beam D′ is:
D′=d√2(2μ2−1)μ
The diameter of the refracted beam is:
D′=dμ√2μ2−1
Topper's Solved these Questions
- RAY OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - medical entrance special format question
23 Videos
- RAY OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - Medical entrance gallary
76 Videos
- RAY OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - Checkpoint 9.7
10 Videos
- NUCLEIBOOK - DC PANDEY ENGLISHCHAPTER - NUCLEIEXERCISE - C MADICAL ENTRANCES GALLERY
46 Videos
- REFLECTION OF LIGHTBOOK - DC PANDEY ENGLISHCHAPTER - REFLECTION OF LIGHTEXERCISE - Subjective
9 Videos
Similar Questions
A circular beam of light of diameter d=2cm falls on a plane refractive of glass. The angle of incidence is 60∘ and refractive index of glass is μ=3/2. The diameter of the refracted beam is
View SolutionA circular beam of light of diameter (width) falls on a plane surface of glass. The angle of incidence is .I., angle of refraction is .r. and refractive index of glass is μ. Then the diameter of the refracted beam d. is…….
View Solution
Knowledge Check
A beam of light is incident at the polarizing angle of 35∘ on a certain glass plate. The refractive index of the glass plate is:
Asin35∘Btan35∘Ctan55∘Dsin55∘
A ray of light incidents on a refracting surface at 30∘ with the surface . If the angle of refraction is 45∘ refractive index of the medium is
View SolutionA light of wavelength fall on a plane surface at an angle of incidence 53. The refractive index of surface material, if the reflected light is completely plane polarised is
View SolutionA beam of light strikes a surface at angle of incidence of 60∘ and reflected beam becomes completely polarised . The refractive index of glass surface is -
View SolutionA parallel narrow beam of light is incident on the surface of a transparent hemisphere of radius R and refractive index μ=1.5 as shown. The position of the image formed by refraction at the image formed by refraction at the spherical surface only as
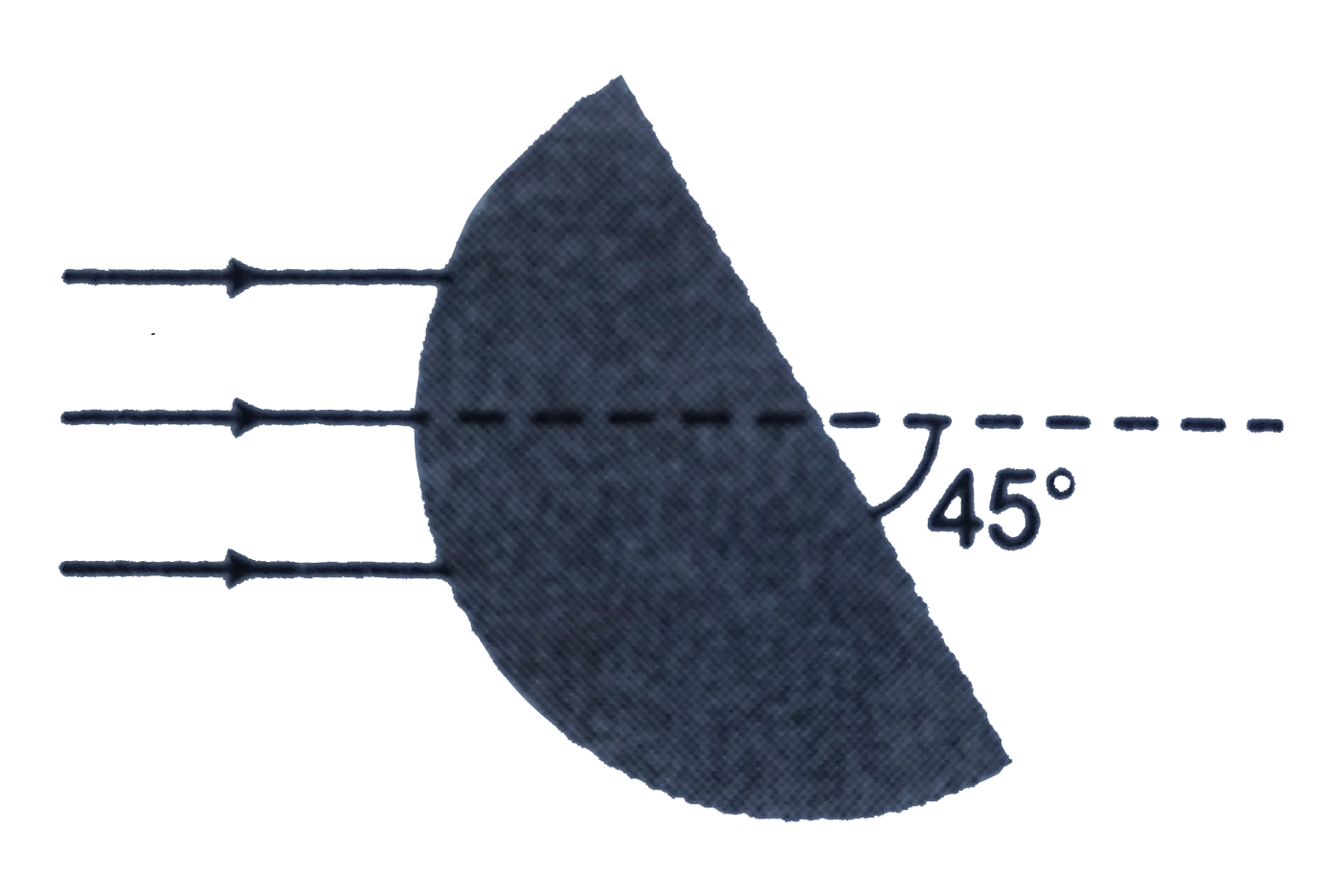
View SolutionWhen light of particular wavelength falls on a plane surface at an angle of incidence 60∘ then the reflected light becomes completely plane polarized Find the refractive index of surface material and the angle of refraction through it.
View SolutionA parallel beam of light falls on a solid tranparent sphere.
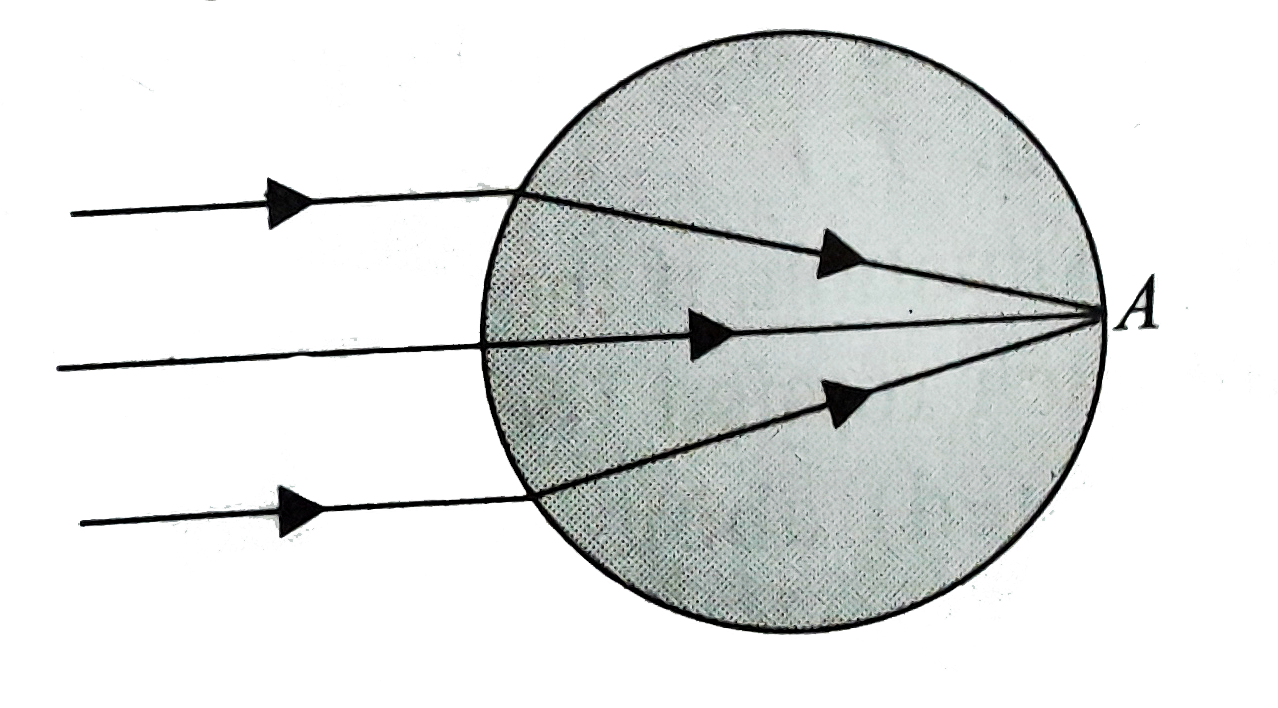
Q. If however thin beam is focussed at A, then find the refractive index of the sphere,
View SolutionUnpolarized light is incident on a plane glass surface having refractive index . The angle of incidence at which reflected and refracted rays would become perpendicular to each other is :
View Solution
