A symmetric double convex lens is cut in two equal parts by a plane perpendiculr to the pricipal axis. If the power of the original lens was 4D, the power of a cut lens will be
a.2D b.3D c.4D d.5D
2D
3D
4D
5D
The correct Answer is:A
To solve the problem step by step, we will analyze the situation of cutting a symmetric double convex lens and how it affects the power of the lens.
1. Understand the Given Data:
- The original lens is a symmetric double convex lens with a power of P=4D.
- The lens is cut into two equal parts by a plane perpendicular to the principal axis.
2. Recall the Formula for Power:
- The power P of a lens is given by the formula:
P=1f
where f is the focal length of the lens.
3. Determine the Focal Length of the Original Lens:
- From the power of the original lens:
4=1f⟹f=14 meters=0.25 meters
4. Understand the Effect of Cutting the Lens:
- When the lens is cut in half, the focal length of each half changes. The new focal length f′ of each half can be derived from the original focal length:
- The focal length of the cut lens is given by:
1f′=μ−1(1R−1∞)
- Since 1∞=0, we have:
1f′=μ−1⋅1R
5. Relate the Focal Lengths:
- For the original lens, we had:
1f=(μ−1)(1R−(−1R))=(μ−1)⋅2R
- Therefore, when the lens is cut, the new focal length f′ becomes:
f′=2f
6. Calculate the Power of the Cut Lens:
- The power of the cut lens P′ can now be calculated as:
P′=1f′=12f
- Since we know f=0.25 meters, we have:
P′=12×0.25=10.5=2D
7. Final Answer:
- The power of the cut lens is 2D.
Conclusion:
The power of the cut lens will be 2D.
- The original lens is a symmetric double convex lens with a power of P=4D.
- The lens is cut into two equal parts by a plane perpendicular to the principal axis.
- The power P of a lens is given by the formula:
P=1f
where f is the focal length of the lens.
- From the power of the original lens:
4=1f⟹f=14 meters=0.25 meters
- When the lens is cut in half, the focal length of each half changes. The new focal length f′ of each half can be derived from the original focal length:
- The focal length of the cut lens is given by:
1f′=μ−1(1R−1∞)
- Since 1∞=0, we have:
1f′=μ−1⋅1R
- For the original lens, we had:
1f=(μ−1)(1R−(−1R))=(μ−1)⋅2R
- Therefore, when the lens is cut, the new focal length f′ becomes:
f′=2f
- The power of the cut lens P′ can now be calculated as:
P′=1f′=12f
- Since we know f=0.25 meters, we have:
P′=12×0.25=10.5=2D
- The power of the cut lens is 2D.
The power of the cut lens will be 2D.
Topper's Solved these Questions
- RAY OPTICSBook:DC PANDEY ENGLISHChapter:RAY OPTICSExercise:medical entrance special format question
Explore 23 Videos
- RAY OPTICSBook:DC PANDEY ENGLISHChapter:RAY OPTICSExercise:Medical entrance gallary
Explore 76 Videos
- RAY OPTICSBook:DC PANDEY ENGLISHChapter:RAY OPTICSExercise:Checkpoint 9.7
Explore 10 Videos
- NUCLEIBook:DC PANDEY ENGLISHChapter:NUCLEIExercise:C MADICAL ENTRANCES GALLERY
Explore 46 Videos
- REFLECTION OF LIGHTBook:DC PANDEY ENGLISHChapter:REFLECTION OF LIGHTExercise:Subjective
Explore 9 Videos
Similar Questions
A symmetric double convex lens is cut in two equal parts by a plane perpendicular to the principal axis. If the power of the original lens was 4D, the power of a cut lens will be
View SolutionThe power of a lens is -5 D.
Name the type of lens.
View SolutionA thin double convex lens is cut into two equal pieces A and B by a plane containing principal axis. The piece B is further cut into two more pieces pieces C and D by another plane perpendicular to the principal axis. If the focal power of the original lens is P, then thos of A and C are
View SolutionA thin, symmetric double convex lens of power P is cut into three parts A, B, and C as shown in Figure. The power of
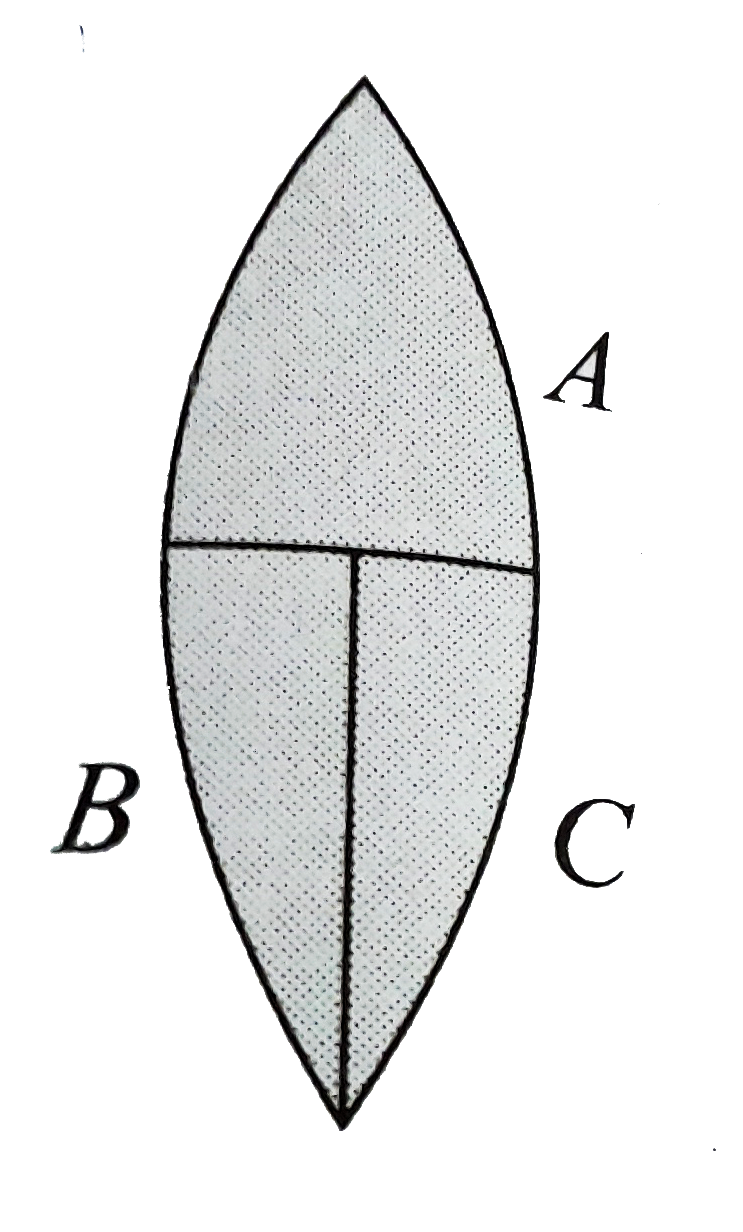
View SolutionA thin symmetrical double convex lens of power P is cut into three parts, as shown in the figure. Power of A is

View SolutionThe two surfaces of a biconvex lens has same radii of curvatures . This lens is made of glass of refractive index 1.5 and has a focal length of 10 cm in air. The lens is cut into two equal halves along a plane perpendicular to its principal axis to yield two plane - convex lenses. The two pieces are glued such that the convex surfaces touch each other. If this combination lens is immersed in water (refractive index =43 ), its focal length (in cm ) is
View SolutionThe power of a lens is -5 D.
Find its focal length.
View SolutionTwo convex lenses of power 2 D and 3 D are separated by a distance 13m. The power of the optical system formed is
View SolutionThe source is placed 30 cm from a convex lens which has a focal length of 20cm. The source is initially located on the axis of the lens. The lens is then cut into two halves in a plane along the principal axis. The two halves are separated by a distance of 4mm. What will be the locations of the image of the source?
View SolutionA convex lens of power 4D is kept in contact with a concave lens of power 3D, the effective power of combination will be
View Solution