A ball is thrown vertically upwards with a velocity of from the top of a multistore building of 25 m high. How high will the ball rise? (Take g = )
Let us take the Y-axis in the vertically upwards direction with zero at the ground.
Now,
If the ball rises to height y from the point of launch, then using the eqution
We get
Solving, we get,
There are two ways of solving the problem
Method I - We split two parts the upwards motion (A to B) and the dowanward motion (B to C) and calculate the corresponding time taken and .
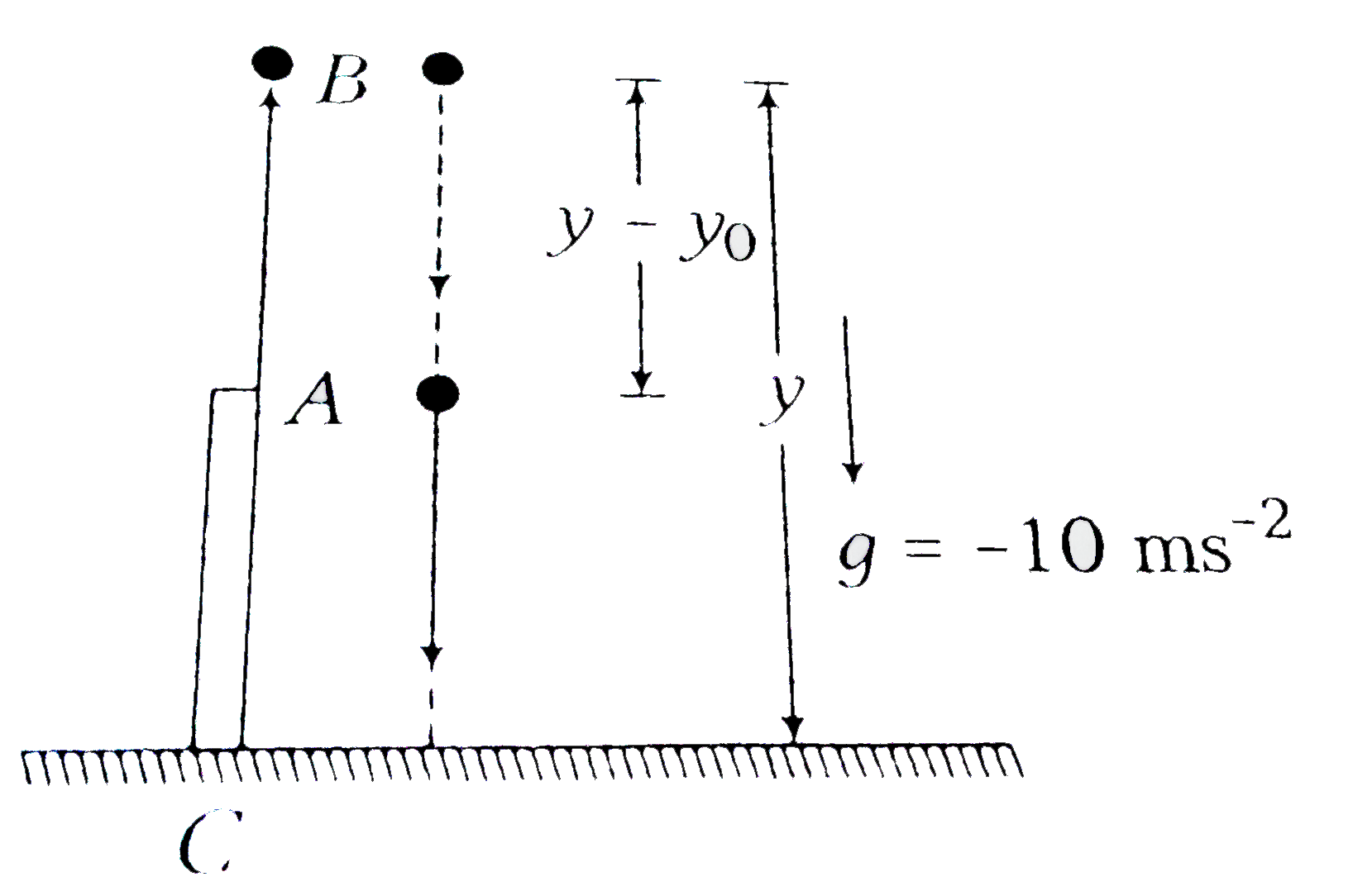
Since, the velocity at B is zero, we have
This is the time in in going from A to B. From B or the point of the maximum height, the ball falls freely under the y-direction . We use equation
We have,
Total time taken by the ball before it hits the ground
Method II- The total time taken can also be calculated by noting the coordinates of initial and final positions of the ball with respect to the origin chosen and using equation
Now,
Solving this quadratic equation for t, we get
t = 5 s
Note - The second method is better since we do not have to worry about the path of the motion as the motion is under constant acceleration.
Topper's Solved these Questions
- MOTION IN A PLANEBook:DC PANDEY ENGLISHChapter:MOTION IN A PLANEExercise:Check point 3.1
Explore 10 Videos
- MOTION IN A PLANEBook:DC PANDEY ENGLISHChapter:MOTION IN A PLANEExercise:Check point 3.2
Explore 10 Videos
- MOTIONBook:DC PANDEY ENGLISHChapter:MOTIONExercise:Medical entrances gallery
Explore 19 Videos
- PROJECTILE MOTIONBook:DC PANDEY ENGLISHChapter:PROJECTILE MOTIONExercise:Level - 2 Subjective
Explore 10 Videos
Similar Questions
A ball is thrown vertically upwards with a velocity of 20ms−1 from the top of a multistorey building. The height of the point from where the ball is thrown is 25.0 m from the ground. (a) How high will the ball rise ? and (b) how long will it be before the ball hits the ground ? Take g=10ms−2.
View SolutionA ball is thrown vertically upwards with a velcotiy of 20ms−1 from the top of a multi-storey building. The height of the point fromwher the ball is thrown if 25m from the ground. (a) How high the ball will rise ? And (b) how long will it be before the ball hits the ground ? Take. g=10ms−2.
View Solution
Knowledge Check
A ball is thrown vertically upwards with a velcotiy of 20ms−1 from the top of a multi-storey building. The height of the point fromwher the ball is thrown if 25m from the ground. (a) How high the ball will rise ? And (b) how long will it be before the ball hits the ground ? Take. g=10ms−2.
A10 mB15 mC45 mD25 m
A ball is projected horizontally with a velocity of 5ms−1 from the top of a building 19.6m high. How long will the ball take to hit the ground ?
View SolutionA ball is thrown downwards with a speed of 20ms−1, from the top of a building 150m high and simultaneously another ball is thrown vertically upwards with a speed of 30ms−1 from the foot to the building . Find the time after which both the balls will meet. (g=10 m s^(-2))
 .
.
View SolutionA ball is thrown vertically upward with a velocity of 20 m/s. Calculate the maximum height attain by the ball.
View SolutionA ball is throw vertically upward. It has a speed of 10m/s when it has reached on half of its maximum height. How high does the ball rise ? (Taking g=10m/s2).
View SolutionA ball thrown vertically upwards with an initial velocity of 1.4m/s. The total displcement of the ball is
View SolutionA ball is throuwn with a speed of 20 m//s from top of a buling 150 m high and simultaneously another ball is thrown vertically upward witn a speed of 30 m/s from the foot of the builing . Find the time when both the balls will meet (g=10m/s2)
View SolutionA pebble is thrown vertically upwards with a speed of 20 m s−1. How high will it be after 2 s? (Take g = 10 m s−2)
View Solution