A ball is throw vertically upward. It has a speed of 10m/s when it has reached on half of its maximum height. How high does the ball rise ? (Taking g=10m/s2).
5m
15m
10m
20m
The correct Answer is:C
To solve the problem of how high the ball rises when thrown vertically upward with an initial speed of 10ms at half of its maximum height, we can follow these steps:
1. Understanding the Problem:
- The ball is thrown vertically upward.
- It reaches a speed of 10ms at half of its maximum height (H2).
- We need to find the maximum height H.
2. Using the Third Equation of Motion:
- At the maximum height, the final velocity (v) is 0ms.
- The initial velocity (u) at half the maximum height is 10ms.
- The acceleration due to gravity (g) is 10ms² (acting downwards).
3. Applying the Equation:
- We can use the third equation of motion:
\(
v^2 = u^2 - 2gH
\)
- For the maximum height, we can set this up as:
\(
0 = u^2 - 2gH
\)
- Rearranging gives:
\(
u^2 = 2gH \quad \text{(Equation 1)}
\)
4. Finding the Velocity at Half the Maximum Height:
- Now, we consider the motion when the ball is at half the maximum height (H2).
- Here, the initial velocity (u) is 10ms and the final velocity (v) is also 10ms (the speed when it reaches H2).
- We use the same equation:
\(
v^2 = u^2 - 2g\left(\frac{H}{2}\right)
\)
- Plugging in the values gives:
\(
10^2 = u^2 - gH
\)
- This simplifies to:
\(
100 = u^2 - gH \quad \text{(Equation 2)}
\)
5. Substituting Equation 1 into Equation 2:
- From Equation 1, we know:
\(
u^2 = 2gH
\)
- Substitute this into Equation 2:
\(
100 = 2gH - gH
\)
- This simplifies to:
\(
100 = gH
\)
6. Solving for Maximum Height (H):
- Now, substituting the value of g:
\(
100 = 10H
\)
- Dividing both sides by 10 gives:
\(
H = 10 \text{ meters}
\)
Final Answer:
The maximum height to which the ball rises is 10 meters.
- The ball is thrown vertically upward.
- It reaches a speed of 10ms at half of its maximum height (H2).
- We need to find the maximum height H.
- At the maximum height, the final velocity (v) is 0ms.
- The initial velocity (u) at half the maximum height is 10ms.
- The acceleration due to gravity (g) is 10ms² (acting downwards).
- We can use the third equation of motion:
\(
v^2 = u^2 - 2gH
\)
- For the maximum height, we can set this up as:
\(
0 = u^2 - 2gH
\)
- Rearranging gives:
\(
u^2 = 2gH \quad \text{(Equation 1)}
\)
- Now, we consider the motion when the ball is at half the maximum height (H2).
- Here, the initial velocity (u) is 10ms and the final velocity (v) is also 10ms (the speed when it reaches H2).
- We use the same equation:
\(
v^2 = u^2 - 2g\left(\frac{H}{2}\right)
\)
- Plugging in the values gives:
\(
10^2 = u^2 - gH
\)
- This simplifies to:
\(
100 = u^2 - gH \quad \text{(Equation 2)}
\)
- From Equation 1, we know:
\(
u^2 = 2gH
\)
- Substitute this into Equation 2:
\(
100 = 2gH - gH
\)
- This simplifies to:
\(
100 = gH
\)
- Now, substituting the value of g:
\(
100 = 10H
\)
- Dividing both sides by 10 gives:
\(
H = 10 \text{ meters}
\)
The maximum height to which the ball rises is 10 meters.
Similar Questions
An object is thrown vertically upward with a speed of 30 m/s. The velocity of the object half-a-second before it reaches the maximum height is
View SolutionA ball is projected vertically up with speed 20 m/s. Take g=10m/s2
View SolutionA ball is thrown vertically upwards from the ground with a speed of 25.2ms−1. How long does it take to reach its highest point and how high does it rise ? (Take g=9.8ms−2)
View SolutionA ball is projected vertically up wards with a velocity of 100 m/s. Find the speed of the ball at half the maximum height. (g=10m/s2)
View SolutionA ball is throuwn with a speed of 20 m//s from top of a buling 150 m high and simultaneously another ball is thrown vertically upward witn a speed of 30 m/s from the foot of the builing . Find the time when both the balls will meet (g=10m/s2)
View SolutionA ball is thrown downwards with a speed of 20ms−1, from the top of a building 150m high and simultaneously another ball is thrown vertically upwards with a speed of 30ms−1 from the foot to the building . Find the time after which both the balls will meet. (g=10 m s^(-2))
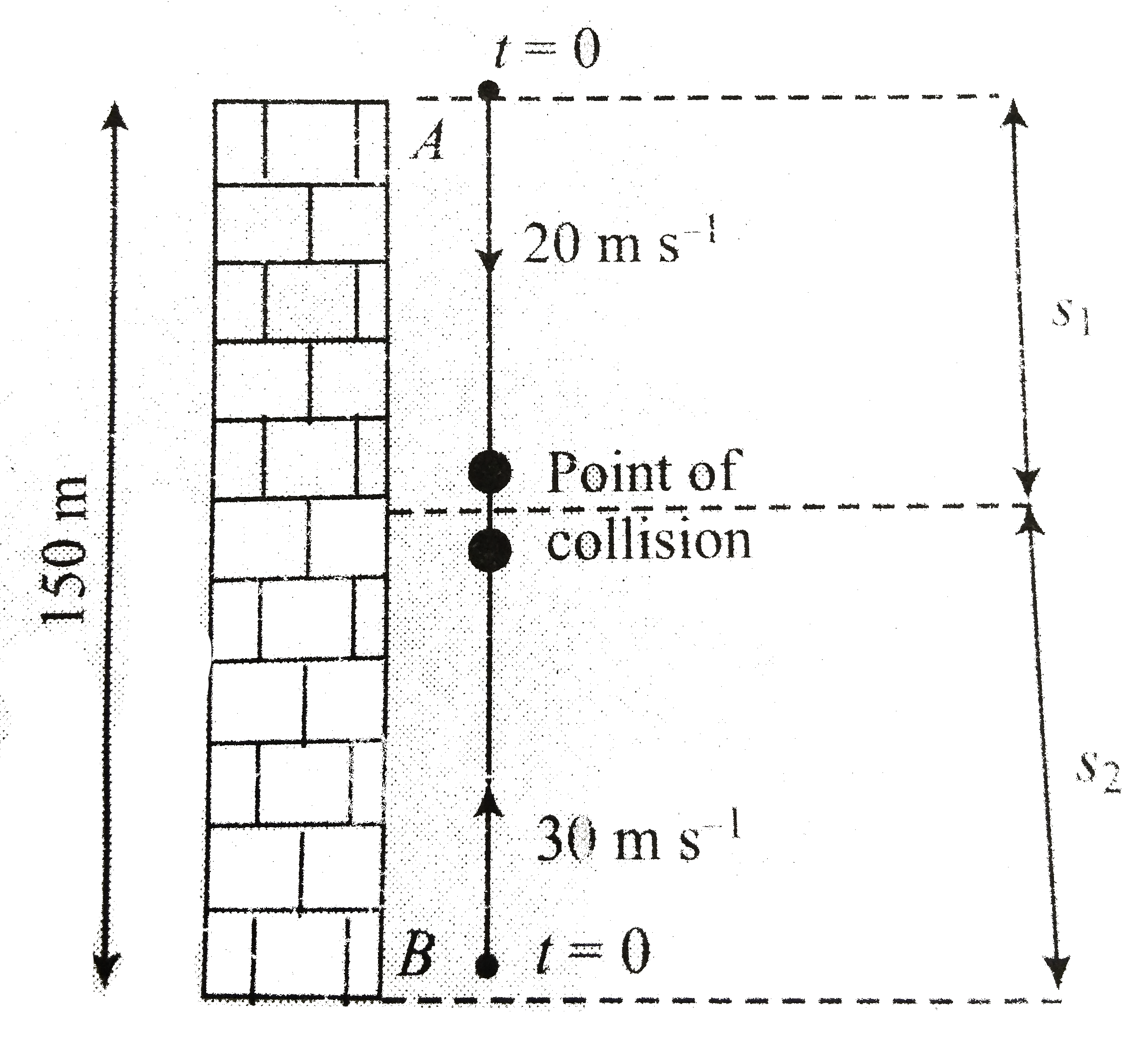 .
.
View SolutionA ball is thrown vertically upward with a velocity of 20 m/s. Calculate the maximum height attain by the ball.
View SolutionA ball is thrown vertically upwards. It returns 6 s later. Calculate the greatest height reached by the ball
View SolutionA ball is thrown at a speed of 20 m/s at an angle of 30∘ with the horizontal . The maximum height reached by the ball is
(Use g=10m/s2)
View SolutionA ball of mas 2gm is thrown vertically upwards with a speed of 30m/s from a tower of height 35m. (Given g=10m/s2)
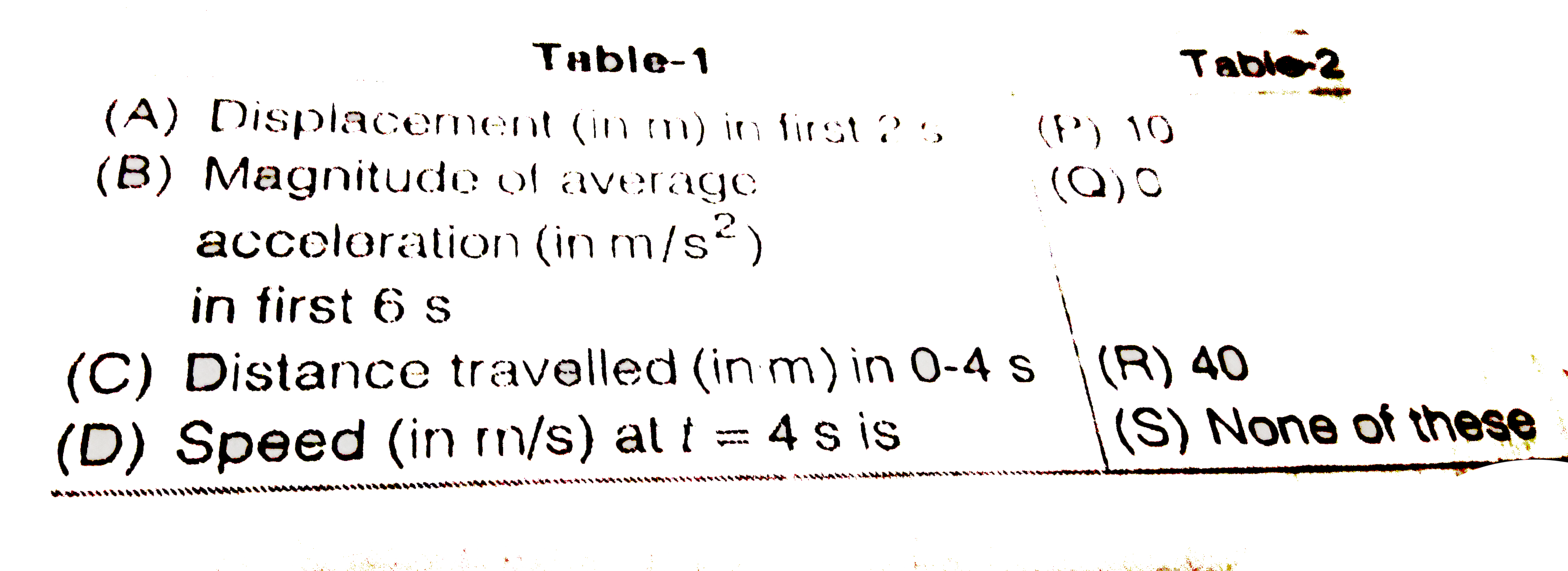
View Solution
