If a disc of mass m and radius r is reshaped into a ring of radius, the mass remining the same, the radius of gyration about centrodal axis perpendicular to plane goes up by a factor of
2
4
The correct Answer is:C
To solve the problem, we need to determine the radius of gyration of both the disc and the ring and then find the factor by which the radius of gyration increases when the disc is reshaped into a ring.
Step 1: Calculate the Radius of Gyration for the Disc
The formula for the radius of gyration kd of a disc about an axis perpendicular to its plane through its center is given by:
kd=√Idm
where Id is the moment of inertia of the disc and m is its mass.
The moment of inertia Id of a disc is given by:
Id=12mr2
Substituting this into the equation for kd:
kd=√12mr2m=√12r2=r√12=r√2
Step 2: Calculate the Radius of Gyration for the Ring
Now, we need to find the radius of gyration kr of the ring. The ring has a radius of 2r and the mass m remains the same.
The moment of inertia Ir of a ring about an axis perpendicular to its plane through its center is given by:
Ir=mR2
For our ring, R=2r:
Ir=m(2r)2=4mr2
Now, substituting this into the equation for kr:
kr=√Irm=√4mr2m=√4r2=2r
Step 3: Find the Factor by which the Radius of Gyration Increases
Now, we need to find the factor by which the radius of gyration increases when the disc is reshaped into a ring:
Factor=krkd=2rr√2
Simplifying this:
Factor=2r⋅√2r=2√2
Conclusion
The radius of gyration about the centroidal axis perpendicular to the plane goes up by a factor of 2√2.
---
Topper's Solved these Questions
- ROTATIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONEXERCISE - (B) Chapter Exercises
25 Videos
- ROTATIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONEXERCISE - (C) Chapter Exercises
39 Videos
- ROTATIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONEXERCISE - Check point 9.3
15 Videos
- RAY OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - Integer type q.
14 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Subjective Questions
2 Videos
Similar Questions
If a disc of mass m and radius r is reshaped into a ring a radius 2r,the mass remaining the same, the radius of gyration about centroidal axis perpendicular to plane goes up by a factor of √x . Find the value of x.
View SolutionIf a disc of moment of inertia I and radius r is reshaped into a ring of radius nr, keeping its mass same, its moment of inertia becomes
View Solution
Knowledge Check
Two thin discs each of mass M and radius r metre are attached to form a rigid body as shown in figure. The rotational inertia of this body about an axis perpendicular to the plane of disc B and passing through its centre is
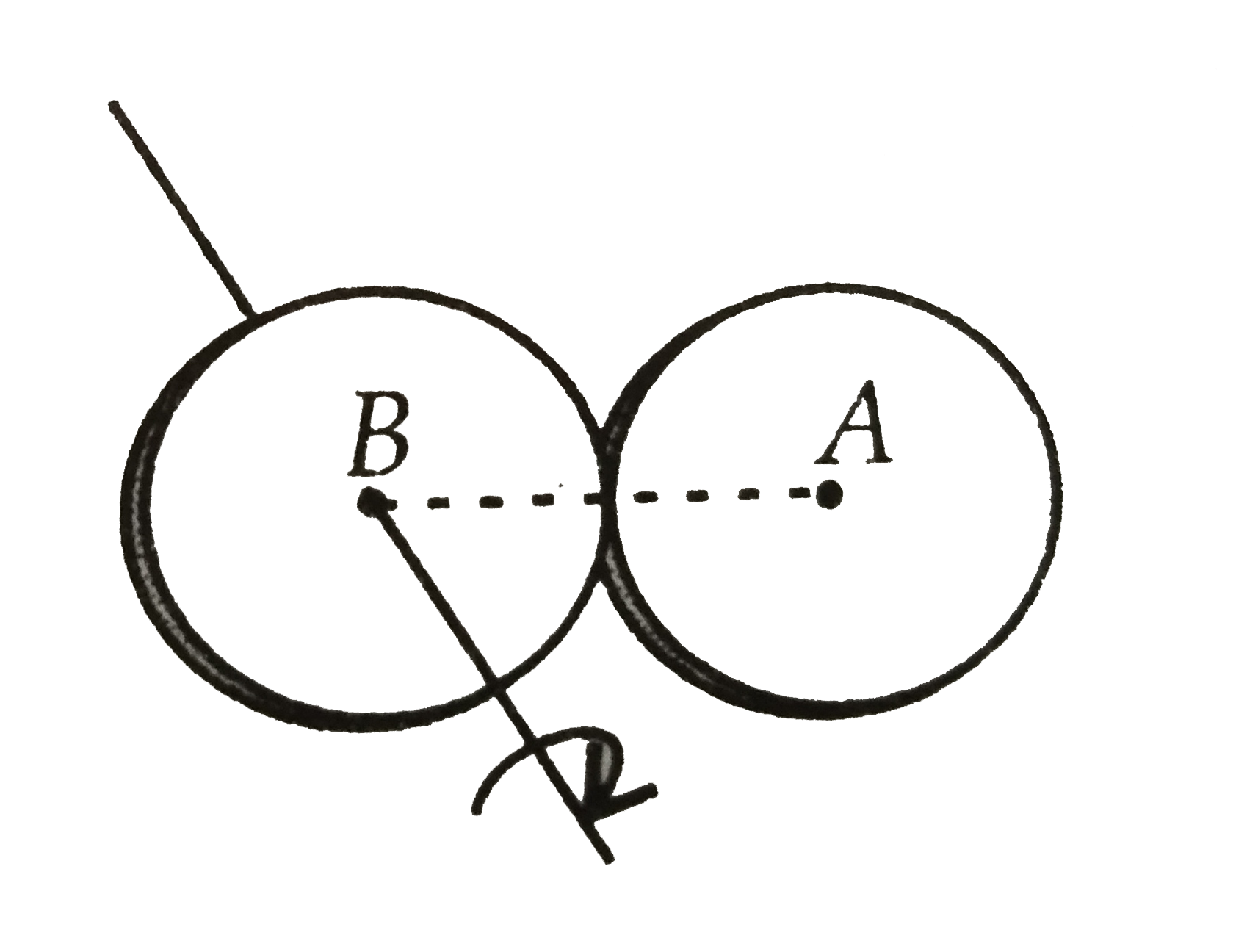 A2Mr2B3Mr2C4Mr2D5Mr2
A2Mr2B3Mr2C4Mr2D5Mr2
The M.I. of a ring of mass M and radius R about a tangential axis perpendicular to its plane is :
View SolutionA disc of mass m and radius R has a concentric hole of radius r. Its moment of inertia about an axis through its center and perpendicular to its plane is
View SolutionA disc of radius R is pivoted at its rim. The period for small oscillations about an axis perpendicular to the plane of disc is
View SolutionA disc of radius R has a concentric hole of radius R /2 and its mass is M. Its moment of inertia about an axis through its centre and perpendicular to its plane, is
View SolutionThe ratio of the radii of gyration of a circular disc and a circular ring of the same radii about a tangential axis perpendicular to plane of disc or ring is
View SolutionSurface mass density of disc of mass m and radius R is Kr2. Then its moment of inertia w.r.t. axis of rotation passing through center and perpendicular to the plane of disc is :
View SolutionMoment of inertia of a ring of mass M and radius R about an axis passing through the centre and perpendicular to the plane is
View Solution
