Consider three solid spheres, sphere (i) has radius r and mass m, sphere (ii) has radius r and mass 3 m, sphere (iii) has radius 3r and mass m, All can be placed at the same point on the same inclined plane, where they will roll without slipping to the bottom, If allowed to roll down the incline, then at the bottom of the incline
sphere (i) will have the largest speed
sphere (ii) will havethe largest speed
sphere (iii) will have the largest kinetic energy
all the sphere will have equal speeds.
The correct Answer is:D
To solve the problem, we will analyze the motion of the three solid spheres as they roll down an inclined plane using the principle of conservation of energy.
1. Identify the Initial Potential Energy:
Each sphere starts from the same height h on the inclined plane. The potential energy (PE) at the top for each sphere can be expressed as:
PE=mgh
For sphere (i), it is mgh; for sphere (ii), it is 3mgh; and for sphere (iii), it is mgh.
2. Set Up the Energy Conservation Equation:
As the spheres roll down the incline, their potential energy converts into kinetic energy (KE). The total kinetic energy at the bottom consists of translational kinetic energy and rotational kinetic energy:
KE=12mv2+12Iω2
where I is the moment of inertia and ω is the angular velocity. For a solid sphere, the moment of inertia I is given by:
I=25mr2
and the relationship between linear velocity v and angular velocity ω is:
ω=vr
3. Calculate for Each Sphere:
- Sphere (i): Mass m, Radius r
mgh=12mv2+12(25mr2)(vr)2
Simplifying gives:
mgh=12mv2+15mv2
mgh=710mv2
Cancel m:
gh=710v2⟹v2=10gh7⟹v=√10gh7
- Sphere (ii): Mass 3m, Radius r
3mgh=12(3m)v2+12(25(3m)r2)(vr)2
Simplifying gives:
3mgh=32mv2+35mv2
3mgh=2110mv2
Cancel 3m:
gh=710v2⟹v2=10gh7⟹v=√10gh7
- Sphere (iii): Mass m, Radius 3r
mgh=12mv2+12(25m(3r)2)(v3r)2
Simplifying gives:
mgh=12mv2+65mv2
mgh=710mv2
Cancel m:
gh=710v2⟹v2=10gh7⟹v=√10gh7
4. Conclusion:
From the calculations, we find that all three spheres have the same final speed at the bottom of the incline:
v=√10gh7
Thus, the answer is that all spheres will have equal speed at the bottom of the incline.
Each sphere starts from the same height h on the inclined plane. The potential energy (PE) at the top for each sphere can be expressed as:
PE=mgh
For sphere (i), it is mgh; for sphere (ii), it is 3mgh; and for sphere (iii), it is mgh.
As the spheres roll down the incline, their potential energy converts into kinetic energy (KE). The total kinetic energy at the bottom consists of translational kinetic energy and rotational kinetic energy:
KE=12mv2+12Iω2
where I is the moment of inertia and ω is the angular velocity. For a solid sphere, the moment of inertia I is given by:
I=25mr2
and the relationship between linear velocity v and angular velocity ω is:
ω=vr
- Sphere (i): Mass m, Radius r
mgh=12mv2+12(25mr2)(vr)2
Simplifying gives:
mgh=12mv2+15mv2
mgh=710mv2
Cancel m:
gh=710v2⟹v2=10gh7⟹v=√10gh7
3mgh=12(3m)v2+12(25(3m)r2)(vr)2
Simplifying gives:
3mgh=32mv2+35mv2
3mgh=2110mv2
Cancel 3m:
gh=710v2⟹v2=10gh7⟹v=√10gh7
mgh=12mv2+12(25m(3r)2)(v3r)2
Simplifying gives:
mgh=12mv2+65mv2
mgh=710mv2
Cancel m:
gh=710v2⟹v2=10gh7⟹v=√10gh7
From the calculations, we find that all three spheres have the same final speed at the bottom of the incline:
v=√10gh7
Thus, the answer is that all spheres will have equal speed at the bottom of the incline.
Topper's Solved these Questions
- ROTATIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONEXERCISE - (B) Chapter Exercises
25 Videos
- ROTATIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONEXERCISE - (C) Chapter Exercises
39 Videos
- ROTATIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONEXERCISE - Check point 9.3
15 Videos
- RAY OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - Integer type q.
14 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Subjective Questions
2 Videos
Similar Questions
A ring of mass m and radius R is placed on a rough inclined plane so that it rolls without slipping . Match the following table.


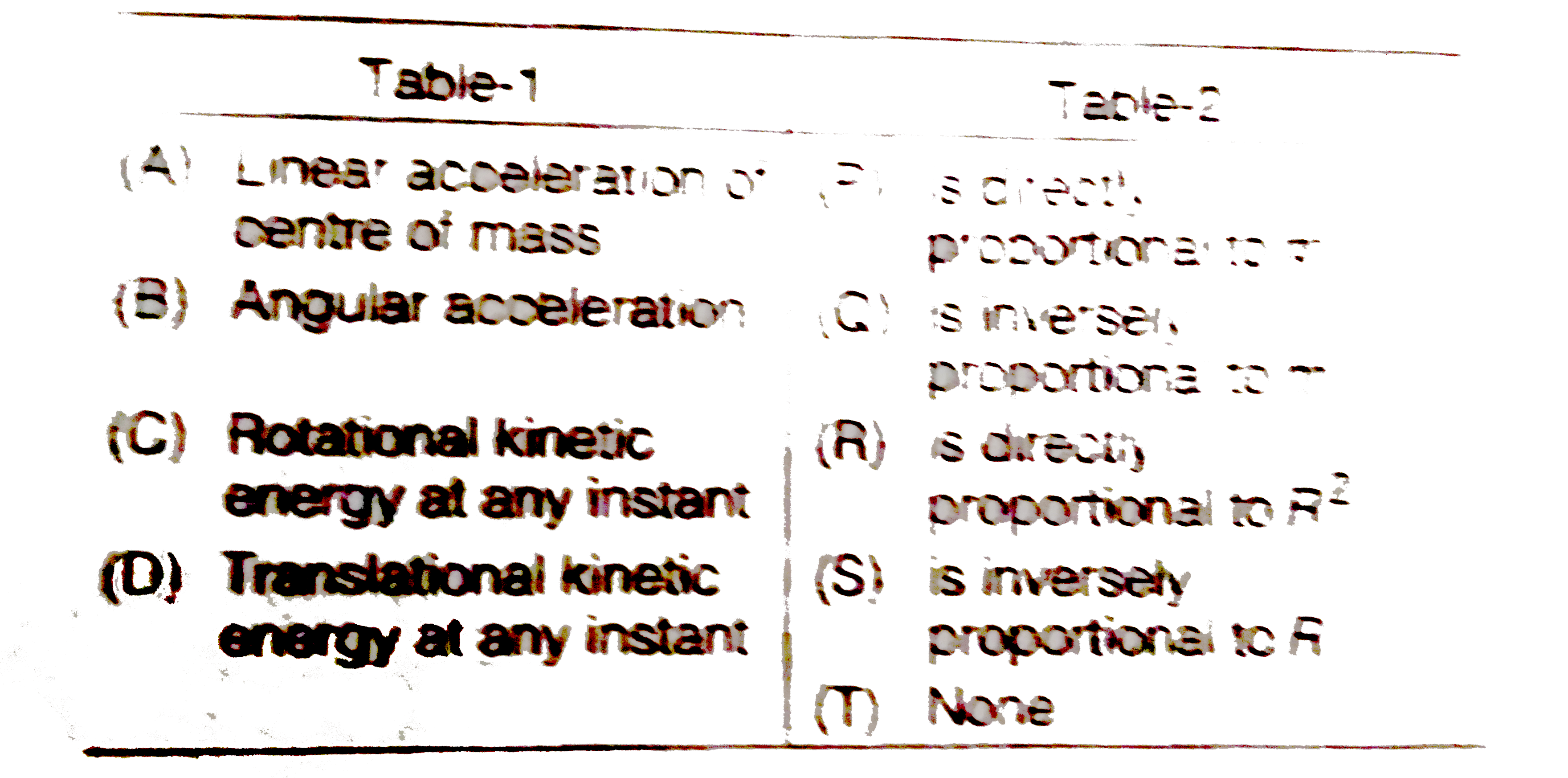
View SolutionA sphere and circular disc of same mass and radius are allowed to roll down an inclined plane from the same height without slipping. Find the ratio of times taken by these two to come to the bottom of incline :
View Solution
Knowledge Check
A hollow sphere and a solid sphere both having the same mass of 5 kg and radius 10 m are initially at rest. If they are made to roll down the same inclined plane without slipping, the ratio of their speeds when they reach the bottom of the plane VhollowVsolid, will be
A1B7√10C7√12D21√25

A solid sphere of mass M and radius R is hit by a cue at a height h above the centre C. for what value of h the sphere will rool without slipping ?
View SolutionA hollow sphere is released from top of an inclined plane of inclination 30º and length of inclined plane is /. If sphere rolls without slipping then its speed at bottom is
View SolutionA solid sphere, disc and solid cylinder, all of the same mass, are allowed to roll down (from rest) on inclined plane, them
View SolutionA drum of radius R and mass M, rolls down without slipping along an inclined plane of angle θ. The frictional force-
View SolutionA disc and a solid sphere of same radius but different masses roll off on two inclined planes of the same altitude and length. Which one of the two objects gets to the bottom of the plane first ?
View SolutionA disc and a solid sphere of same radius but different masses roll off on two inclined planes of the same altitude and length. Which one of the two objects gets to the bottom of the plane first ?
View SolutionA solid sphere is rolling down an inclined plane without slipping of height 20 m. Calculate the maximum velocity with which it will reach the bottom of the plane (g=10m/s2)
View Solution
