In the figure, a point object O is placed in air. A spherical boundry separates two media of radius of curvature 1.0m. AB is principal axis. The separation between the images formed due to refraction at spherical surface is
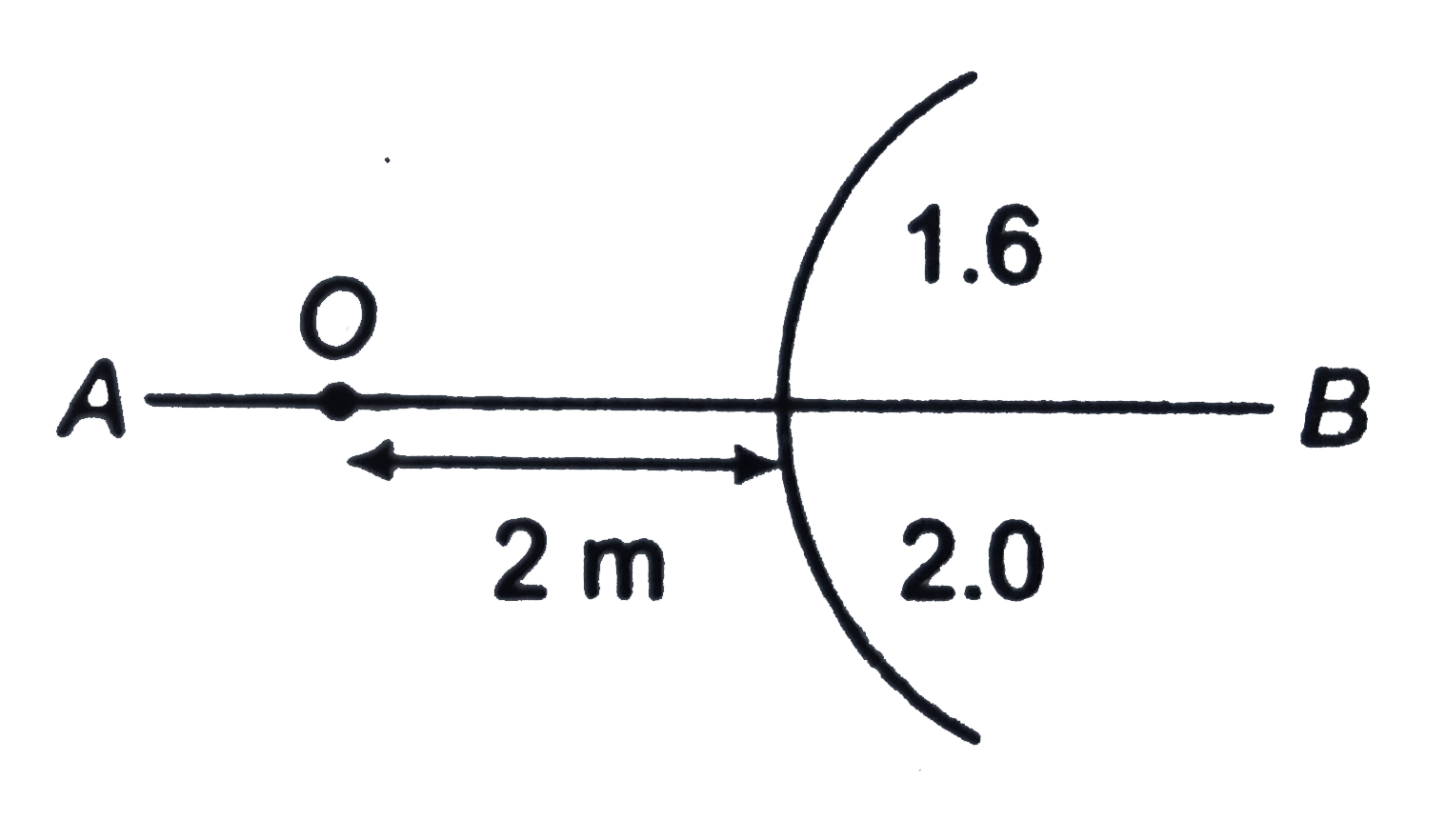
12m
20m
14m
10m
The correct Answer is:A
1.6v1−1.0−2=1.6−1.0+10
rArr v1=16cm
2.0v2−1.0−2=2.0−1.0+10
∴v2=4m
I2I2=v1−v2
=12cm
Topper's Solved these Questions
- REFRACTION OF LIGHTBook:DC PANDEY ENGLISHChapter:REFRACTION OF LIGHTExercise:Single Correct Option
Explore 3 Videos
- REFRACTION OF LIGHTBook:DC PANDEY ENGLISHChapter:REFRACTION OF LIGHTExercise:more than one correct option
Explore 1 Video
- REFRACTION OF LIGHTBook:DC PANDEY ENGLISHChapter:REFRACTION OF LIGHTExercise:Subjective Questions
Explore 8 Videos
- REFLECTION OF LIGHTBook:DC PANDEY ENGLISHChapter:REFLECTION OF LIGHTExercise:Subjective
Explore 9 Videos
- SEMICONDUCTORSBook:DC PANDEY ENGLISHChapter:SEMICONDUCTORSExercise:Subjective
Explore 12 Videos
Similar Questions
In Figure, a point object O is placed in air. A spherical boundary separates two media. Ab is the principall axis. The refractive index above AB is 1.6 and below AB is 2.0. The separation between the images formed due to refraction at a the spherical surface is (assume the radius of curvature (R) to be 1 unit)
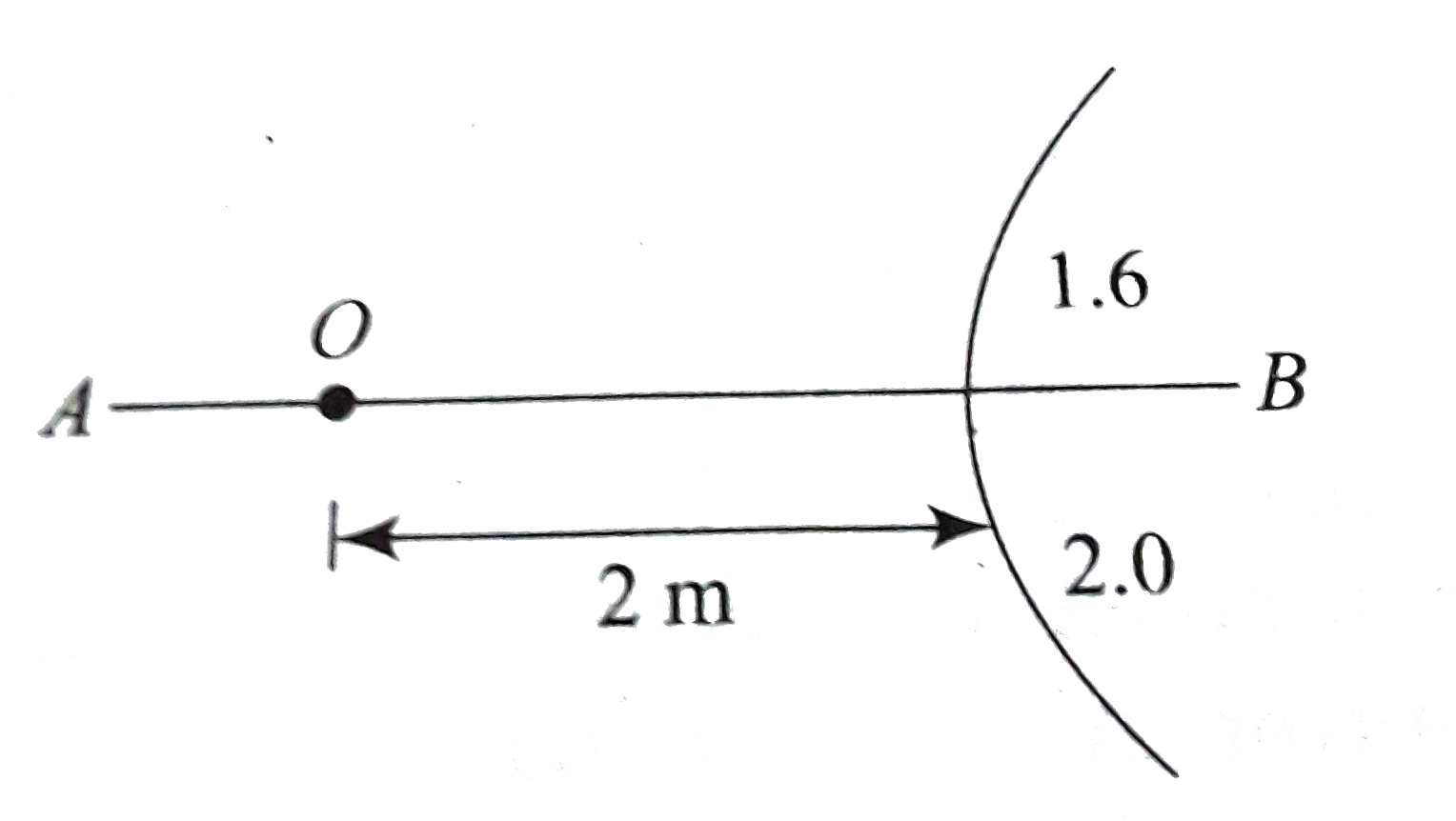
View SolutionIn the figure shown , a point object O is placed in air on the principal axis. The radius of curvature of the spherical surfaces is 60cm. I is the final image formed after all reflections and refractions.
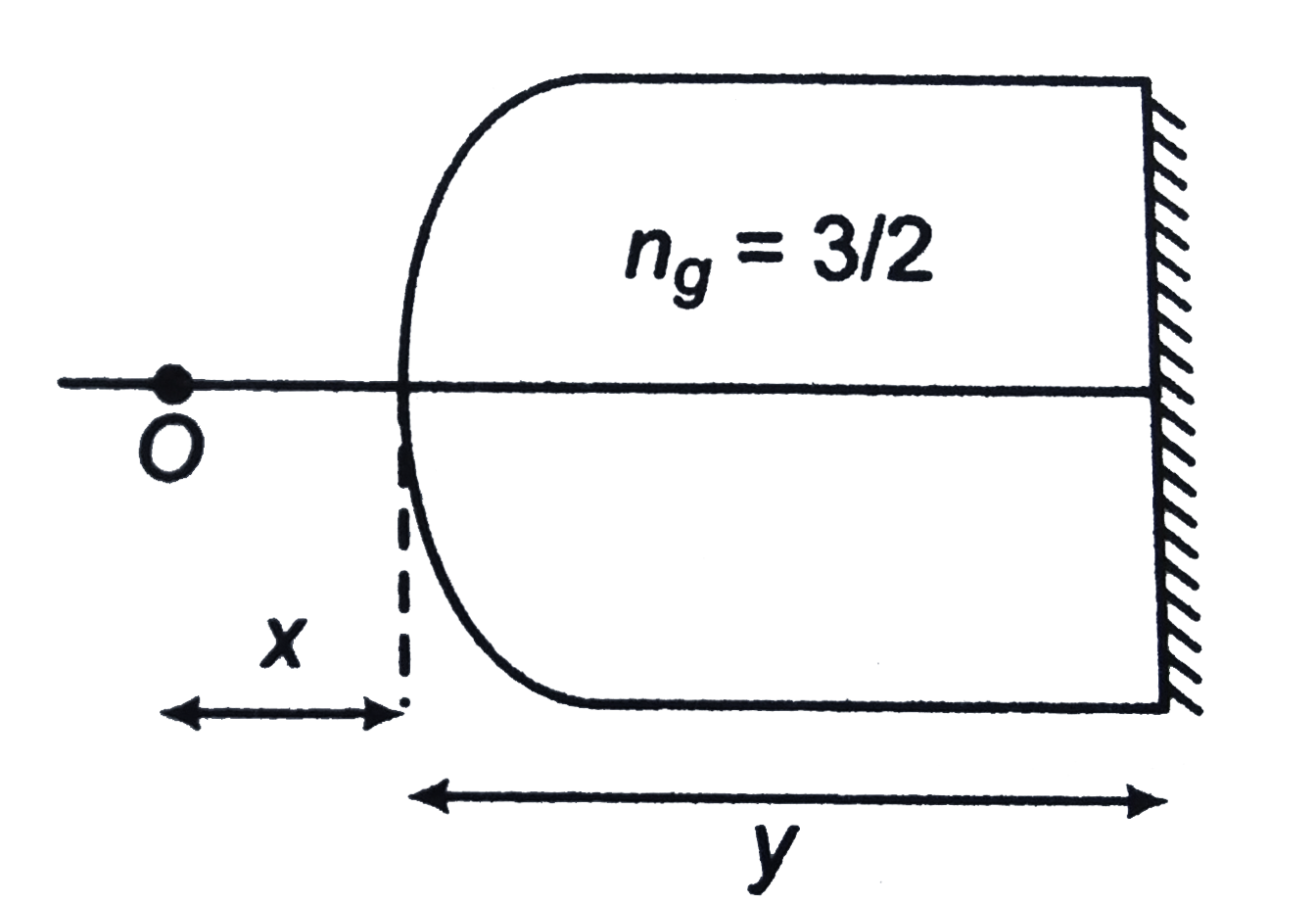
View SolutionAn object is placed 10cm away form a glass piece (n=1.5) of length 20cm bounded by spherical surfaces of radii of curvaure 10cm. Find the position of final image formed after two refractions at the spherical surfaces.
View SolutionA poinit object O is placed in front of a glass rod having spherical end of radius of curvature 30cm. The image would be formed at
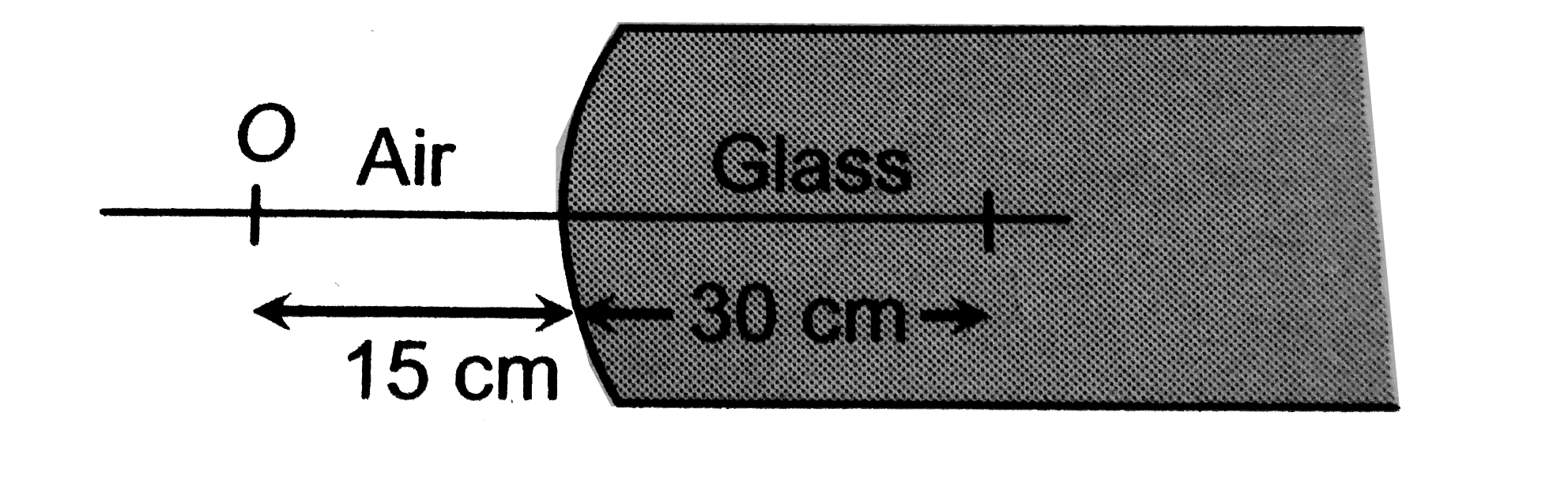
View SolutionA poinit object O is placed in front of a glass rod having spherical end of radius of curvature 30cm. The image would be formed at

View SolutionTrace the rays of light showing the formation of an image due to a point object placed on the axis of a spherical surface separating the two media of refractive indices n1andn2. Establish the relation between the distance of the object, the image and the radius of curvature from the central point of the spherical surface.
Hence derive the expression of the lens maker's formula
View SolutionAn object 5 cm tall is placed 1 m from a concave spherical mirror which has a radius of curvature of 20 cm. The size of the image is
View SolutionAn object 5 cm tall is placed 1 m from a concave spherical mirror which has a radius of curvature of 20 cm. The size of the image is
View Solution(a) A point object, O is on the principle axis of a spherical surface having a radius of curvature, R. Draw a diagram to obtain the relation between the object and image distances, the refractive indicess of the media and the radius of curvature of the spherical surface.
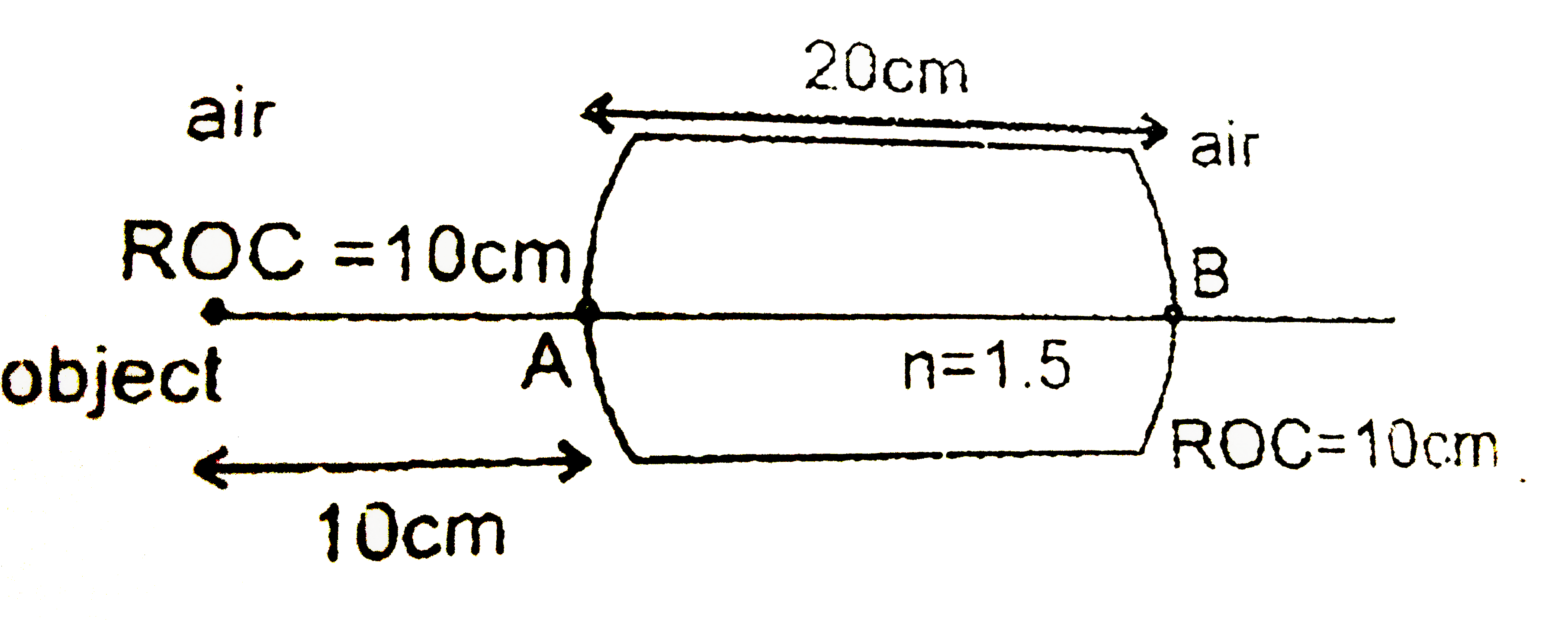
View SolutionFigure below shows a parallel beam of monochromatic light incident on a convex spherical surface, radius of curvature R = 30 cm, which separates glass (refractive index - 1 6) from air. Find the position of the image formed due to refraction of light at this single spherical surface.

View Solution