(a) A point object, O is on the principle axis of a spherical surface having a radius of curvature, R. Draw a diagram to obtain the relation between the object and image distances, the refractive indicess of the media and the radius of curvature of the spherical surface.
To solve the problem, we need to establish the relationship between the object distance (u), image distance (v), refractive indices (n1 and n2), and the radius of curvature (R) of a spherical surface. Here’s a step-by-step solution:
Step 1: Draw the Ray Diagram
1. Draw the Principal Axis: Start by drawing a horizontal line representing the principal axis.
2. Draw the Spherical Surface: Draw a spherical surface (concave or convex) with the center of curvature (C) marked. The radius of curvature (R) is the distance from the center of curvature to the surface.
3. Mark the Object: Place a point object O on the principal axis, to the left of the spherical surface.
4. Draw the Image: Indicate where the image (I) is formed on the principal axis, to the right of the spherical surface.
Step 2: Define Distances and Angles
1. Object Distance (u): Measure the distance from the object O to the pole (P) of the spherical surface. This distance is taken as negative in the sign convention (u = -|u|).
2. Image Distance (v): Measure the distance from the pole (P) to the image I. This distance is positive (v = +|v|).
3. Radius of Curvature (R): The distance from the center of curvature (C) to the pole (P) of the spherical surface is R.
Step 3: Apply Geometry to Find Angles
1. Angle of Incidence (I): Draw a normal line at the point of incidence on the spherical surface. The angle between the incoming ray and the normal is the angle of incidence (I).
2. Angle of Refraction (r): The angle between the refracted ray and the normal is the angle of refraction (r).
Step 4: Use Trigonometric Relationships
1. For the Object Side: From the geometry, we can write:
- tan(α)=Pu (where P is the height of the object).
- tan(I−α)=PR.
- For small angles, tan can be approximated as sin and cos.
2. For the Image Side: Similarly, we can write:
- tan(x)=Pv (where x is the angle related to the image).
- tan(I−α−r)=PR.
Step 5: Apply Snell's Law
1. Snell's Law states that n1sin(I)=n2sin(r).
2. For small angles, this can be approximated as:
- n1I=n2r.
Step 6: Combine the Equations
1. Substitute the expressions for I and r from the previous steps into Snell's Law.
2. Rearranging gives us a relationship involving u, v, n1, n2, and R:
- n1u+n2v=n2−n1R.
Final Relationship
The final relationship can be expressed as:
n2v−n1u=n2−n1R
1. Draw the Principal Axis: Start by drawing a horizontal line representing the principal axis.
2. Draw the Spherical Surface: Draw a spherical surface (concave or convex) with the center of curvature (C) marked. The radius of curvature (R) is the distance from the center of curvature to the surface.
3. Mark the Object: Place a point object O on the principal axis, to the left of the spherical surface.
4. Draw the Image: Indicate where the image (I) is formed on the principal axis, to the right of the spherical surface.
1. Object Distance (u): Measure the distance from the object O to the pole (P) of the spherical surface. This distance is taken as negative in the sign convention (u = -|u|).
2. Image Distance (v): Measure the distance from the pole (P) to the image I. This distance is positive (v = +|v|).
3. Radius of Curvature (R): The distance from the center of curvature (C) to the pole (P) of the spherical surface is R.
1. Angle of Incidence (I): Draw a normal line at the point of incidence on the spherical surface. The angle between the incoming ray and the normal is the angle of incidence (I).
2. Angle of Refraction (r): The angle between the refracted ray and the normal is the angle of refraction (r).
1. For the Object Side: From the geometry, we can write:
- tan(α)=Pu (where P is the height of the object).
- tan(I−α)=PR.
- For small angles, tan can be approximated as sin and cos.
- tan(x)=Pv (where x is the angle related to the image).
- tan(I−α−r)=PR.
1. Snell's Law states that n1sin(I)=n2sin(r).
2. For small angles, this can be approximated as:
- n1I=n2r.
1. Substitute the expressions for I and r from the previous steps into Snell's Law.
2. Rearranging gives us a relationship involving u, v, n1, n2, and R:
- n1u+n2v=n2−n1R.
The final relationship can be expressed as:
n2v−n1u=n2−n1R
Topper's Solved these Questions
- XII BOARDSBOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - XII BOARDSEXERCISE - C.B.S.E.CLASS-XII PHYSICS (THEORY) [SET-I]
3 Videos
- XII BOARDSBOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - XII BOARDSEXERCISE - Section -A
14 Videos
- XII BOARDSBOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - XII BOARDSEXERCISE - SECTIONS-E
4 Videos
- SAMPLE PAPER 2019BOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - SAMPLE PAPER 2019EXERCISE - SECTION D
6 Videos
Similar Questions
Trace the rays of light showing the formation of an image due to a point object placed on the axis of a spherical surface separating the two media of refractive indices n1andn2. Establish the relation between the distance of the object, the image and the radius of curvature from the central point of the spherical surface.
Hence derive the expression of the lens maker's formula
View Solution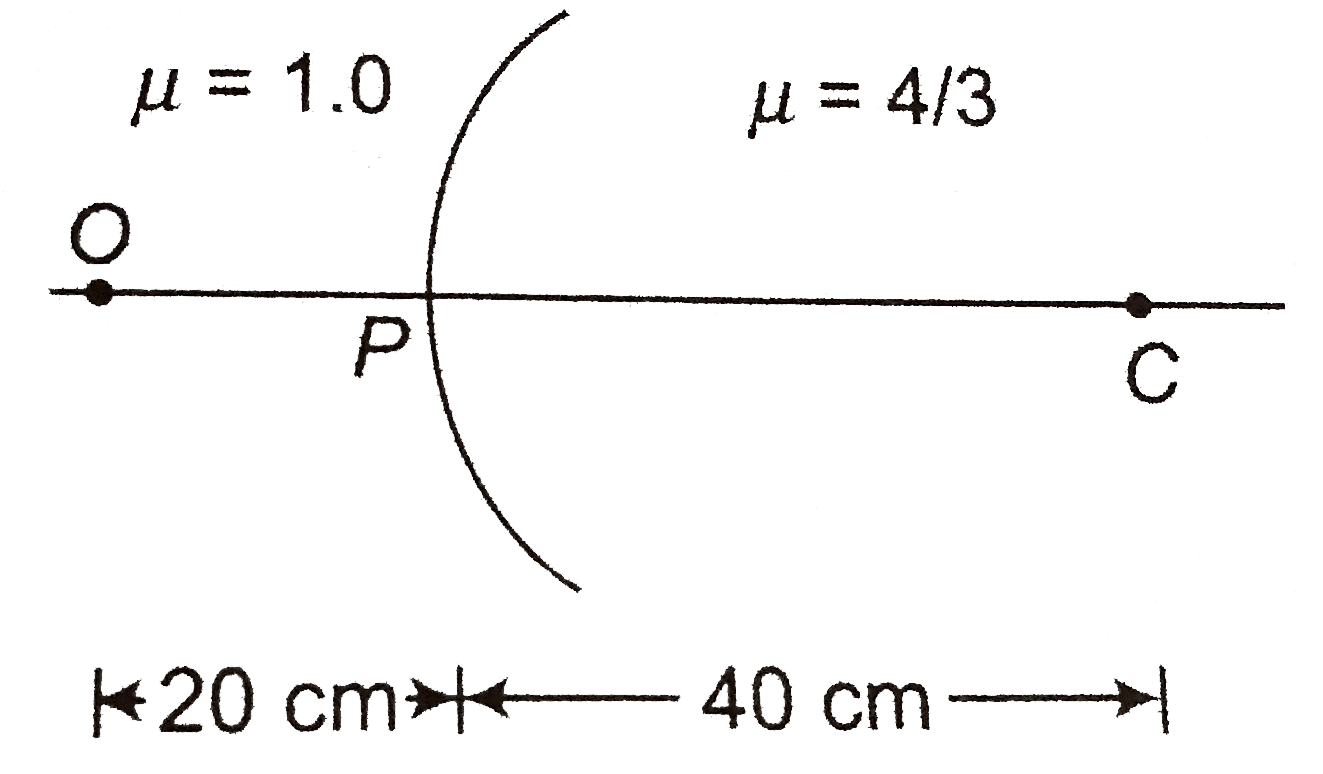
Locate the image of the point object O. The point C is centre of curvature of the spherical surface.
View SolutionHow is the focal length of a spherical mirror related to its radius of curvature?
View SolutionA spherical convex surface separates object and image space of refractive index 1.0and43. If radius of curvature of the surface is 10cm, find its power.
View SolutionA spherical convex surface separates object and image space of refractive index 1.0and43. If radius of curvature of the surface is 10cm, find its power.
View SolutionA poinit object O is placed in front of a glass rod having spherical end of radius of curvature 30cm. The image would be formed at
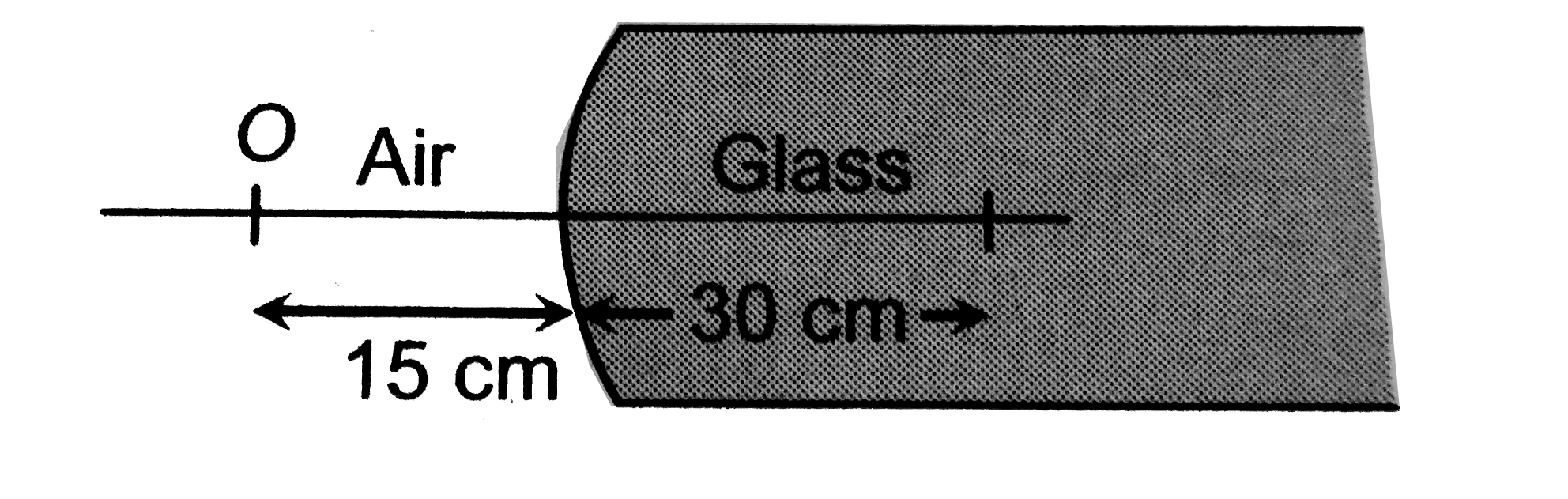
View SolutionA poinit object O is placed in front of a glass rod having spherical end of radius of curvature 30cm. The image would be formed at

View SolutionIn the figure, a point object O is placed in air. A spherical boundry separates two media of radius of curvature 1.0m. AB is principal axis. The separation between the images formed due to refraction at spherical surface is

View SolutionA point object is placed in front of a silvered plano convex lens of refractive index n radius of curvature R, so that its image is formed on itself. Then the object distance is equal to

View SolutionRadius of curvature of first surface of double convex lens is three times that of the other. If focal length of the lens is 30 cm and refractive index of the lens is 3/2, then radius of curvature of the first surface is
View Solution
