How does the electric flux due to a point charge enclosed by a spherical Gaussian surface get a affected when its radius is increased ?
To understand how the electric flux due to a point charge enclosed by a spherical Gaussian surface is affected when its radius is increased, we can follow these steps:
1. Identify the Point Charge:
- Consider a point charge Q located at the center of a spherical Gaussian surface of radius r.
2. Apply Gauss's Law:
- According to Gauss's Law, the electric flux ΦE through a closed surface is given by:
ΦE=Qencϵ0
- Here, Qenc is the charge enclosed by the Gaussian surface, and ϵ0 is the permittivity of free space.
3. Calculate the Electric Flux:
- For our spherical Gaussian surface of radius r, since the point charge Q is enclosed, the electric flux is:
ΦE=Qϵ0
4. Increase the Radius of the Gaussian Surface:
- Now, consider increasing the radius of the Gaussian surface to 2r (or any larger value). The point charge Q remains at the center.
5. Reapply Gauss's Law:
- The new Gaussian surface still encloses the same charge Q. Therefore, the electric flux through the new surface is:
ΦE=Qϵ0
6. Conclusion:
- Since the charge enclosed by the Gaussian surface has not changed, the electric flux remains the same regardless of the increase in the radius of the Gaussian surface. Thus, we conclude that:
The electric flux remains constant and is independent of the radius of the Gaussian surface.
- Consider a point charge Q located at the center of a spherical Gaussian surface of radius r.
- According to Gauss's Law, the electric flux ΦE through a closed surface is given by:
ΦE=Qencϵ0
- Here, Qenc is the charge enclosed by the Gaussian surface, and ϵ0 is the permittivity of free space.
- For our spherical Gaussian surface of radius r, since the point charge Q is enclosed, the electric flux is:
ΦE=Qϵ0
- Now, consider increasing the radius of the Gaussian surface to 2r (or any larger value). The point charge Q remains at the center.
- The new Gaussian surface still encloses the same charge Q. Therefore, the electric flux through the new surface is:
ΦE=Qϵ0
- Since the charge enclosed by the Gaussian surface has not changed, the electric flux remains the same regardless of the increase in the radius of the Gaussian surface. Thus, we conclude that:
The electric flux remains constant and is independent of the radius of the Gaussian surface.
Topper's Solved these Questions
- XII BOARDSBook:XII BOARD PREVIOUS YEAR PAPER ENGLISHChapter:XII BOARDSExercise:Section -B
Explore 11 Videos
- XII BOARDSBook:XII BOARD PREVIOUS YEAR PAPER ENGLISHChapter:XII BOARDSExercise:Section -C
Explore 7 Videos
- XII BOARDSBook:XII BOARD PREVIOUS YEAR PAPER ENGLISHChapter:XII BOARDSExercise:C.B.S.E.CLASS-XII PHYSICS (THEORY) [SET-I]
Explore 3 Videos
- SAMPLE PAPER 2019Book:XII BOARD PREVIOUS YEAR PAPER ENGLISHChapter:SAMPLE PAPER 2019Exercise:SECTION D
Explore 6 Videos
Similar Questions
A positive charge q is enclosed by a Guassian spherical surface of radius 'a' . If its radius is increased to 4a then the net outward flux will
View SolutionDefine electric flux. Write its SI unit. A charge q is enclosed by a spherical surface of radius R. If the radius is reduced to half, how would the electric flux through the surface change ?
View Solution
Knowledge Check
A point charge 4μC is at the centre of a cubic Gaussian surface 10 cm on edge. Net electric flux through the surface is
A2.5×105Nm2C−1B4.5×105Nm2C−1C4.5×106Nm2C−1D2.5×106Nm2C−1
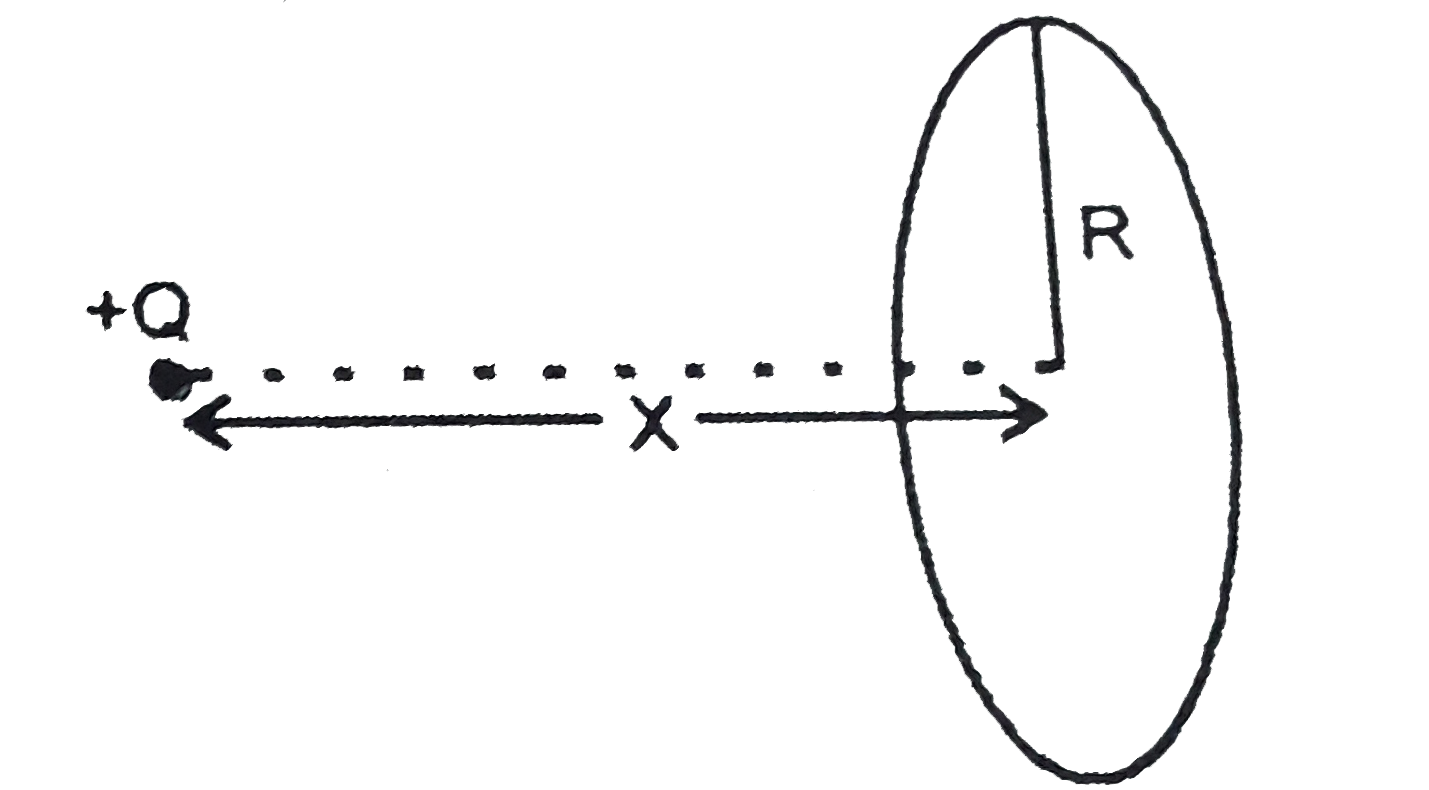
Find the electric flux due to a point charge 'Q' through the circular region of radius R if the charge is placed on the axis of ring at a distance x.
View SolutionIn a region of space having a spherically symmetric distribution of charge, the electric flux enclosed by a concentric spherical Gaussian surface, varies with radius r as
ϕ=ϕ0r3R3 for r≤R
ϕ=ϕ0 for r > R
where R and ϕ0 are constants.
The volume charge density in the region is given as
View SolutionIn a region of space having a spherical symmetic distribution of charge , the electric flux enclosed by a concentric spherical Gaussion surface, varies with radius
r as ϕ={ϕ0r2R3,r≤R<br>ϕ0, <R where R and ϕ0 are the constants.
View SolutionWhich of the following statements is/are correct?
a. Electric field calculated by Gauss law is the field due to only those charges which are enclosed inside the Gaussian surface.
b. Gauss law is applicable only when there is a symmetrical distribution of charge.
c. Electric flux through a closed surface is equal to total flux due to all the charges enclosed within that surface only.
View SolutionA solid insulating sphere of radius a carries a net positive charge 3Q, uniformly distributed throughout its volume. Concentric with this sphere is a conducting spherical shell with inner radius b and outer radius c and having a net charge -Q, as shown in figure

a. Consider a spherical Gaussian surface of radius rgtc, the net charge enclosed by this surface is .............
b. The direction of the electric field rgtc is .............
c. The electric field at rgtc is ............... .
d. The electric field in the region with radius r, which cgtrgtb, is ...............
e. Consider a spherical Gaussian surface of radius r, where c>r>b, the net charge enclosed by this surface is ................ .
f. Consider a spherical Gaussian surface of radius r, whereb>r>a, the net charge enclosed by this surface is ................. .
g. The electric field in the region b>r>a is ................ .
h. Consider a spherical Gaussian surface of radius r<a. Find an expression for the net charge Q(r) enclosed by this surface as a function of r. Note that the charge inside the surface is less than 3Q.
i. The electric field in the region r<a is ................. .
j. The charge on the inner surface of the conducting shell is .......... .
k. The charge on the outer surface of the conducting shell is .............. .
l. Make a plot of the magnitude of the electric field versus r.
View Solutionq1,q2,q3 and q4 are point charges located at point as shown in the figure and s is a spherical Gaussian surface of radius R. Which of the following is true according to the Gauss's law

View SolutionA charge Q is enclosed by a Gaussian spherical surface of radius R. If the radius is doubled, then the outward electric flux will
View Solution

