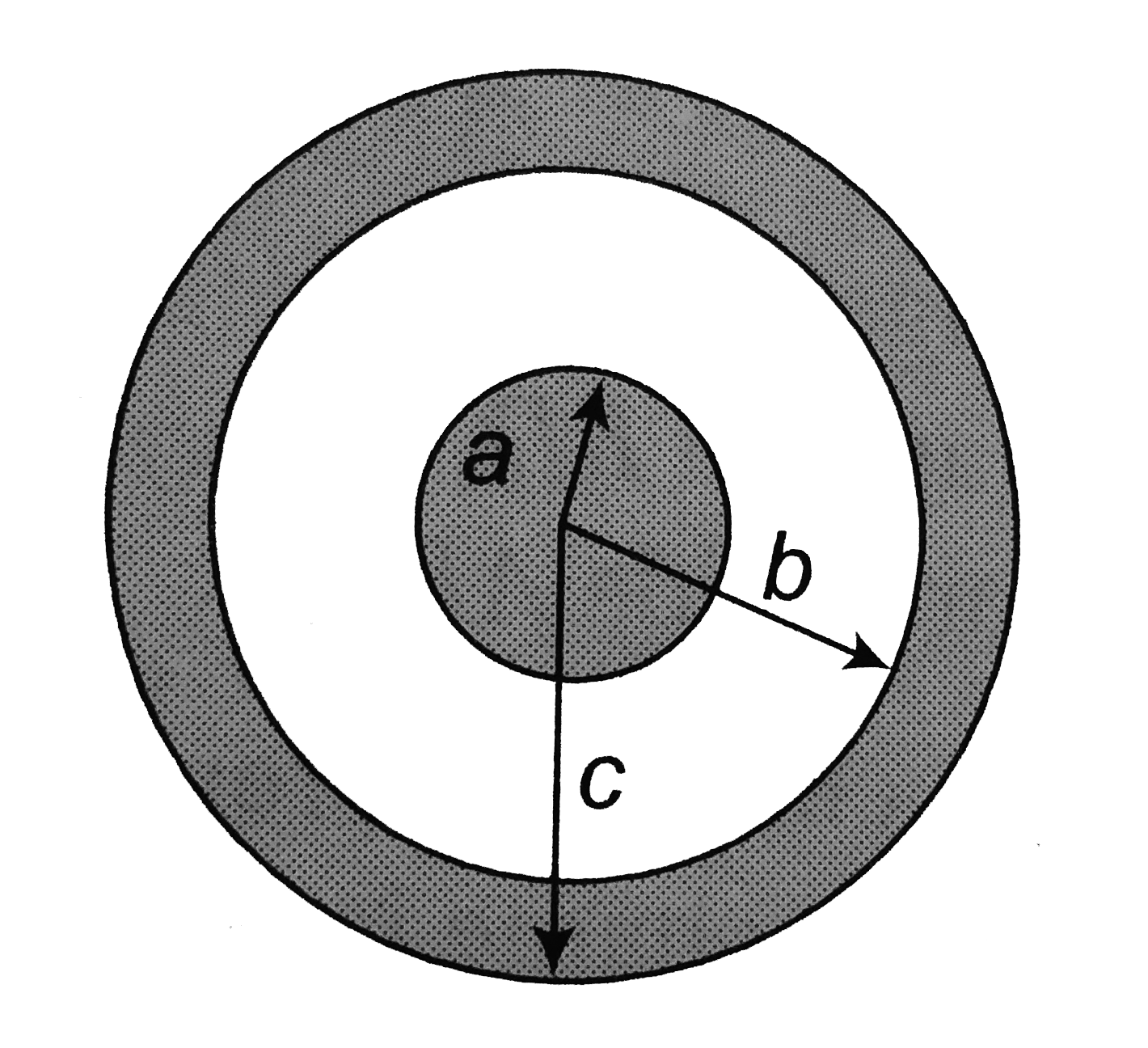
A solid insulating sphere of radius a carries a net positive charge 3Q, uniformly distributed throughout its volume. Concentric with this sphere is a conducting spherical shell with inner radius b and outer radius c and having a net charge -Q, as shown in figure

a. Consider a spherical Gaussian surface of radius rgtc, the net charge enclosed by this surface is .............
b. The direction of the electric field rgtc is .............
c. The electric field at rgtc is ............... .
d. The electric field in the region with radius r, which cgtrgtb, is ...............
e. Consider a spherical Gaussian surface of radius r, where c>r>b, the net charge enclosed by this surface is ................ .
f. Consider a spherical Gaussian surface of radius r, whereb>r>a, the net charge enclosed by this surface is ................. .
g. The electric field in the region b>r>a is ................ .
h. Consider a spherical Gaussian surface of radius r<a. Find an expression for the net charge Q(r) enclosed by this surface as a function of r. Note that the charge inside the surface is less than 3Q.
i. The electric field in the region r<a is ................. .
j. The charge on the inner surface of the conducting shell is .......... .
k. The charge on the outer surface of the conducting shell is .............. .
l. Make a plot of the magnitude of the electric field versus r.
The distribution of charge is as shown in figure.

Net charge enclosed by Gaussian surface (r>c) is 3Q
−3Q+2Q=2Q.
b. For rgtc, the direction of electric field is radially
outward as shown at point A.
c. E=kq∈r2=14πε02Qr2
d. For cltrltb, we have point B. If we draw a Gaussian
surface through B, net charge enclosed in it will be zero.
So electric field at B will be zero.
e. As explained above, net charge enclosed is zero.
f. For bgtrgta, we have point D. If we draw a Gaussian
surface through D, it will have net charge enclosed 3Q.
g. E=kq∈r2=14πε03Qr2
h. ρ=3Q43πa3 (volume charge density)
So, charge with in radius r(<a) is q=ρ43πr3=3Qr3a3
i. E=kq∈r2=14πε03Qr3a3r2=14πε03Qra3
j. As shown in the figure, the charge on the inner surface
of shell is −3Q.
k. As shown in figure, the charge on outer surface of
shell is +2Q.
l.  .
.
Topper's Solved these Questions
- ELECTRIC FLUX AND GAUSS LAWBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - Subjective
12 Videos
- ELECTRIC FLUX AND GAUSS LAWBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - Single Correct
40 Videos
- ELECTRIC FLUX AND GAUSS LAWBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - Exercise 2.1
16 Videos
- ELECTRIC CURRENT AND CIRCUITBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT AND CIRCUITEXERCISE - Interger
8 Videos
- ELECTRIC POTENTIALBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC POTENTIALEXERCISE - DPP 3.5
15 Videos
Similar Questions
A hollow conducting sphere of inner radius r and outer radius 2R is given charge Q as shown in figure, then the

View SolutionA point charge +q is placed at the centre of a conducting spherical shell of inner radius a and outer radius b. Find the charge appearing on the inner and outer surface of the shell.
View SolutionA solid conducting sphere of radius a has a net positive charge 2Q. A conducting spherical shell of inner radius b and outer radius c is concentric with the solid sphere and has a net charge −Q. The surface charge density on the inner and outer surfaces of the spherical shell will be
View SolutionA non-conducting sphere of radius R is given a charge Q. Charge is uniformly distributed in its volume. The electric potential at centre and at the surface of sphere respectively are
View SolutionShown in the figure is a shell made of a conductor. It has inner radius a and outer radius b, and carries charge Q, At its centre is a dipole as show. In this case:
View SolutionA conducting sphere of radius R and a concentric thick spherical shell of inner radius 2R and outer radius 3R is shown in figure. A charge +10Q is given to the shell and inner sphere is earthed. Then charge on inner sphere is

View SolutionA hollow non conducting sphere of radius R has a positive charge q uniformly distributed on its surface. The sphere starts rotating with a constant angular velocity 'ω' about an axis passing through center of sphere, as shown in the figure. Then the net magnetic field at center of the sphere is

View SolutionA metallic spherical shell has an inner radius R1 and outer radius R2. A charge is placed at the centre of the spherical cavity. The surface charge density on the inner surface is

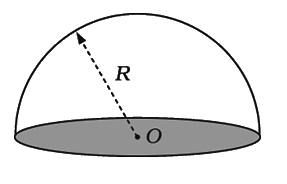
View SolutionCharge Q is uniformly distributed throughout the volume of a solid hemisphere of radius R metres. Then the potential at centre O of hemisphere in volts is:
View SolutionA solid conducting sphere of radius a having a charge q is surrounded by a concentric conducting spherical shell of inner radius 2a and outer radius 3a as shown in figure. Find the amount of heat porduced when switch is closed (k=14πε0)

View Solution
