Consider two concentric conducting spheres. The outer sphere is hollow and initially has a charge −7Q on it. The inner sphere is solid and has a charge +2Q on it.
a. How much charge is on the outer surface and inner surface of the outer sphere.
b. If a wire is connected between the inner and outer sphere, after electrostatic equilibrium is established how much total charge is on the outer sphere? How much charge is on the outer surface and inner surface of the outer sphere? Does the electric field at the surface of the inside sphere change when the wire is connected?
c. We return to original condition in (a). We now connect the outer sphere to ground with a wire and then disconnect it. How much total charge will be on the outer sphere? How much charge will be on the inner surface and outer surface of the outer sphere?
a. The charge on the inner sphere induces eqyal magnitude of charge, but opposite in sign, on the inner surface of the outer sphere. Sum of all the induced charges is always zero. Therefore, an equal amount of charge must appear on the surface. The outer and inner surface of the outer sphere have charges −5Qand−2Q, respectively.
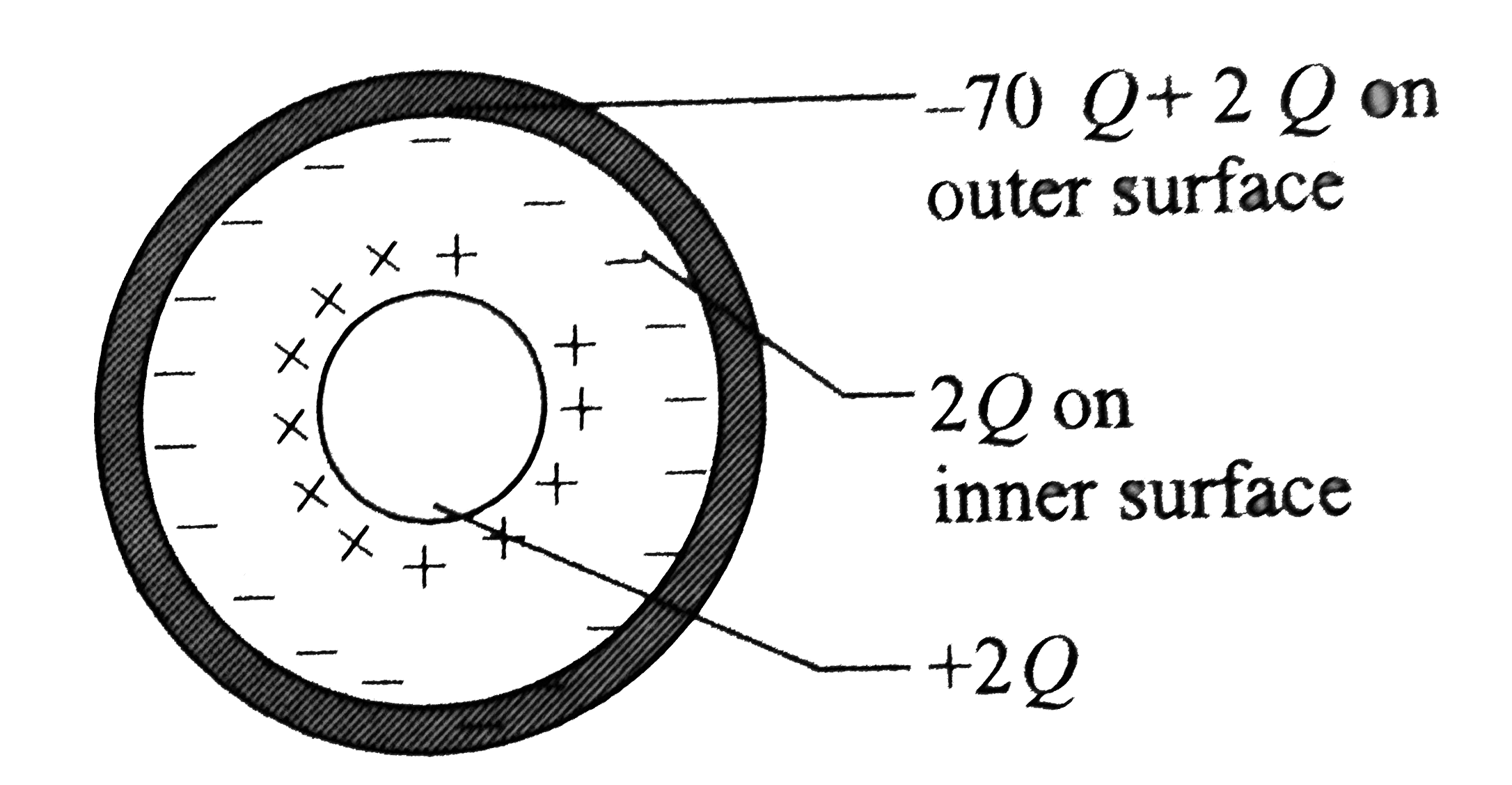
b. When outer and inner spheres are connected by a wire, the entire charge is transferred to the outer surface from the inner sphere. In electrostatic equilibrium, charge does not reside inside a conductor. Total charge on the outer surface of the outer sphere is −5Q.
Total charge on the inner surface is 0.
The electric field at the surface of the inside sphere goes to zero after connection. Consider a Gaussian surface just on the surface of the inner sphere.
ϕE=E(4πr2)=Qenclosedε0=0,asQenclosed=0
Thus, we have E = 0
c. When the outer sphere is grounded the charge on the outer surface is transferred to ground, thus charge is reduced to zero on the outer surface. The final charge distribution is shown in figure.
 .
.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - Subjective12videos
ELECTRIC FLUX AND GAUSS LAW
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - Single Correct40videos
ELECTRIC FLUX AND GAUSS LAW
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - Exercise 2.116videos
ELECTRIC FLUX AND GAUSS LAW
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT AND CIRCUITEXERCISE - Interger8videos
ELECTRIC CURRENT AND CIRCUIT
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC POTENTIALEXERCISE - DPP 3.515videos
ELECTRIC POTENTIAL
Similar Questions
Consider two concentric metal spheres. The outer sphere is given a charge Q>0, then
 ,View Solution
,View SolutionThree concentric conducting spherical shells carry charges as : +4Q on the inner shell, −2Q on the middle shell and −5Q on the outer shell. The charge on the inner surface of the outer shell is
View SolutionThree concentric conducting sphereical shells carry charges +4Q on the inner shell −2Q on the middle shel and +6Q on the outer shell. The charge on the inner surface of the outer shell is
View SolutionCharge on the outer sphere is q, and the inner sphere is grounded. Then the charge q' on the inner sphere is q', for
(r2>r1)
 View Solution
View SolutionThere are three concentric conducting spherical shells. All of them are charged. The innermost sphere is connected by a conducting wire to the outermost sphere. Prove that the final charge on the innermost sphere is independent of the initial charge of outermost sphere.
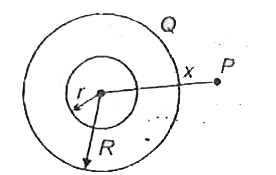
View SolutionTwo concentric hollow conducting spheres of radius r and R are shown. The charge on outer shell is Q. what charge should be given to inner sphere so that the potential at any point P outside the outer sphere is zero ?
 View Solution
View SolutionA spherical capacitor has the inner sphere of radius 2cm and the outerone of 4cm. If the inner sphere is earthed and the outer one is charged with a charge of 2μC and isolated. Calculate ltbr> (a) the potential to which the outer sphere is raised.
(b) the charge retained on the outer surface of the outer sphere.View SolutionAn electric kettle has two coils. When one of these is switched on, thje water in the kettle boils in 6 minutes. When the other coil is switched on, the water boils in 3 minutes. If the two coils are connected in series, the time taken to boil the water in the kettle is
View SolutionStatement-1 : If two concentric conducing sphere which are connected by a conducting wire. No charge can exist on inner sphere.
Statement-2: When charge on outer sphere will exist then potential of inner shell and outer shell will be same.View SolutionA charge Q is placed at the centre of an uncharged, hollow metallic sphere of radius alpha. (a) Find the surface charge density on the inner surface and on the outer surface. (b) If a charge q is put on the sphere, what would be the surface charge densities on the inner and the outer surface?
View Solution
