An object 5 cm tall is placed 1 m from a concave spherical mirror which has a radius of curvature of 20 cm. The size of the image is
0.11 cm
0.5 cm
0.55 cm
0.60 cm
The correct Answer is:C
To find the size of the image formed by a concave mirror, we can use the mirror formula and the magnification formula. Here’s a step-by-step solution:
Step 1: Identify the given values
- Height of the object (h_o) = 5 cm
- Object distance (u) = 1 m = 100 cm (since 1 m = 100 cm)
- Radius of curvature (R) = 20 cm
Step 2: Calculate the focal length (f)
The focal length (f) of a concave mirror is given by the formula:
f=R2
Substituting the value of R:
f=20cm2=10cm
Step 3: Use the sign convention
For a concave mirror:
- The focal length (f) is taken as positive: f=+10cm
- The object distance (u) is also taken as positive: u=+100cm
Step 4: Use the magnification formula
The magnification (m) is given by:
m=hiho=−ff−u
Where:
- hi = height of the image
- ho = height of the object
Step 5: Substitute the values into the magnification formula
We need to find hi:
m=hi5=−1010−100
m=hi5=−10−90
m=hi5=19
Step 6: Solve for the height of the image (h_i)
Now, we can find hi:
hi=m⋅ho
hi=19⋅5
hi=59cm
Step 7: Determine the sign of the image height
Since the magnification is positive, the image is upright. However, in the context of concave mirrors, we typically consider the image to be inverted. Thus:
hi=−59cm
Final Result
The size of the image is approximately:
hi≈−0.55cm
This indicates that the image is inverted and smaller than the object.
---
- Height of the object (h_o) = 5 cm
- Object distance (u) = 1 m = 100 cm (since 1 m = 100 cm)
- Radius of curvature (R) = 20 cm
The focal length (f) of a concave mirror is given by the formula:
f=R2
Substituting the value of R:
f=20cm2=10cm
For a concave mirror:
- The focal length (f) is taken as positive: f=+10cm
- The object distance (u) is also taken as positive: u=+100cm
The magnification (m) is given by:
m=hiho=−ff−u
Where:
- hi = height of the image
- ho = height of the object
We need to find hi:
m=hi5=−1010−100
m=hi5=−10−90
m=hi5=19
Now, we can find hi:
hi=m⋅ho
hi=19⋅5
hi=59cm
Since the magnification is positive, the image is upright. However, in the context of concave mirrors, we typically consider the image to be inverted. Thus:
hi=−59cm
The size of the image is approximately:
hi≈−0.55cm
This indicates that the image is inverted and smaller than the object.
Topper's Solved these Questions
- RAY OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - medical entrance special format question
23 Videos
- RAY OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - Medical entrance gallary
76 Videos
- RAY OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - Checkpoint 9.7
10 Videos
- NUCLEIBOOK - DC PANDEY ENGLISHCHAPTER - NUCLEIEXERCISE - C MADICAL ENTRANCES GALLERY
46 Videos
- REFLECTION OF LIGHTBOOK - DC PANDEY ENGLISHCHAPTER - REFLECTION OF LIGHTEXERCISE - Subjective
9 Videos
Similar Questions
An object 2.5 cm high is placed at a distance of 10 cm from a concave mirror of radius of curvature 30 cm The size of the image is
View SolutionAn object 9.0 mm tall is placed 12.0 cm to the left of the vertex of a convex spherical mirror
whose radius of curvature has a magnitude of 20.0 cm.
(a) Draw a principal ray diagram showing formation of the image.
(b) Determine the position, size, orientation, and nature (real or vertual) of the image.
View SolutionAn object 6.0 mm is placed 16.5 cm to the left of the vertex of a concave spherical mirror having
a radius of curvature of 22.0 cm.
(a) Draw principal ray diagram showing formation of the image.
(b) Determine the position, size, orientation, and nature (real or virtual) of the image.
View SolutionAn object of size 7.5 cm is placed in front of a convex mirror of radius of curvature 25 cm at a distance of 40 cm. The size of the image should be
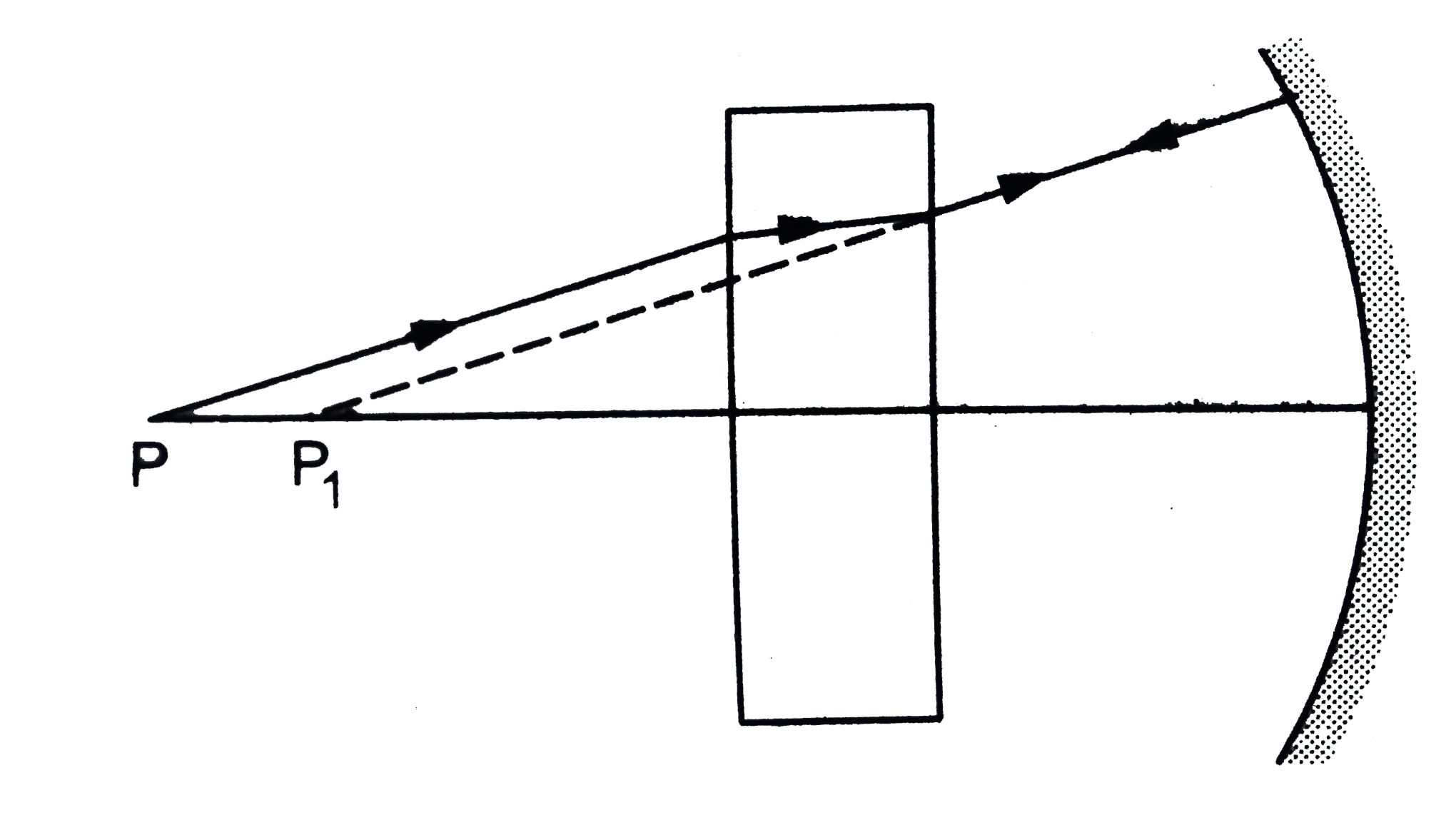
View SolutionAn object is placed 21 cm in fron of a concave mirror of radius of curvature 20 cm.A glass slab of thicknes 3 cm and refractive index 1.5 is palced close to the mirror in the space between the object and the mirror. Find the position of the final image fromed. The distance of the nearer surface of the slab from the mirror is 10 cm.
View SolutionAn object is placed at 4 cm distance in front of a concave mirror of radius of curvature 24 cm. Find the position of image. Is the image magnified?
View SolutionAn object is placed at 21 cm in front of a concave mirror of radius of a curvature 10 cm. A glass slab of thickness 3 cm and u 15 is then placed close to the mirror in the space between the object and the mirror. The position of final image formed is
View SolutionA point object is placed at a distance 20 cm from the focus of a concave mirror of radius of curvature 20 cm. Find the distance (in cm) of the image from the focus.
View SolutionAn object is placed 21 cm in front of a concave mirror of radius of curvature 10cm. A glass slabe of thickness 3cm and refractive index 1.5 is then placed close to the irror in the space between the object and the mirror. The distance of the near surface of the slabe from the mirror is 1cm. The final image from the mirror will be formed at
View SolutionAn object 5.0cm in length is placed at a distance of 20cm in front of a convex mirror of radius of curvature 30cm. Find the position of image, its nature and size.
View Solution
