An object is moving towards a converging lens on its axis. The image is also found to be moving towards the lens. Then, the object distance u must satisfy
2f<u<4f
f<u<2f
u>4f
u<f
The correct Answer is:D
To solve the problem, we need to analyze the behavior of a converging lens when an object is moving towards it, and how this affects the image formation.
1. Understanding the Lens System:
- We have a converging lens, which has a focal point (F) and a pole (P). The distance from the pole to the focus is called the focal length (f).
2. Object Movement:
- The object is moving towards the lens along its axis. As the object approaches the lens, we need to determine how the image behaves.
3. Image Formation:
- According to the lens formula:
1f=1v−1u
where v is the image distance and u is the object distance. For a converging lens, both u and v are negative when measured from the lens.
4. Condition for Image Movement:
- The problem states that as the object moves towards the lens, the image also moves towards the lens. This implies that the image distance v must be decreasing (becoming less negative).
5. Position of the Object:
- If the object is placed at the focal point (F), the image is formed at infinity. As the object moves from the focal point towards the lens (P), the image moves from infinity towards the lens.
- Therefore, when the object is between the focus (F) and the pole (P), the image will be formed between the focus and the lens.
6. Conclusion:
- For the image to move towards the lens as the object moves towards it, the object distance u must be less than the focal length f. Thus, we conclude:
u<f
Final Answer:
The object distance u must satisfy u<f.
---
- We have a converging lens, which has a focal point (F) and a pole (P). The distance from the pole to the focus is called the focal length (f).
- The object is moving towards the lens along its axis. As the object approaches the lens, we need to determine how the image behaves.
- According to the lens formula:
1f=1v−1u
where v is the image distance and u is the object distance. For a converging lens, both u and v are negative when measured from the lens.
- The problem states that as the object moves towards the lens, the image also moves towards the lens. This implies that the image distance v must be decreasing (becoming less negative).
- If the object is placed at the focal point (F), the image is formed at infinity. As the object moves from the focal point towards the lens (P), the image moves from infinity towards the lens.
- Therefore, when the object is between the focus (F) and the pole (P), the image will be formed between the focus and the lens.
- For the image to move towards the lens as the object moves towards it, the object distance u must be less than the focal length f. Thus, we conclude:
u<f
The object distance u must satisfy u<f.
Topper's Solved these Questions
- REFRACTION OF LIGHTBOOK - DC PANDEY ENGLISHCHAPTER - REFRACTION OF LIGHTEXERCISE - Single Correct Option
3 Videos
- REFRACTION OF LIGHTBOOK - DC PANDEY ENGLISHCHAPTER - REFRACTION OF LIGHTEXERCISE - more than one correct option
1 Video
- REFRACTION OF LIGHTBOOK - DC PANDEY ENGLISHCHAPTER - REFRACTION OF LIGHTEXERCISE - Subjective Questions
8 Videos
- REFLECTION OF LIGHTBOOK - DC PANDEY ENGLISHCHAPTER - REFLECTION OF LIGHTEXERCISE - Subjective
9 Videos
- SEMICONDUCTORSBOOK - DC PANDEY ENGLISHCHAPTER - SEMICONDUCTORSEXERCISE - Subjective
12 Videos
Similar Questions
A real object is moving toward a fixed spherical mirror. The image
View SolutionAn illuminated object is placed on the principal axis of a converging lens so that real image is formed on the other side of the lens. If the object is shifted a little,
View SolutionAn object is moving towards a moving mirror as shown in the figure. Find speed of image with respect to ground in m/sec.

View SolutionWhat will be the image speed if
(i) Object is moving towards the plane mirror with speed v ?
(ii) The plane mirror is moving towards the object with speed v ?
View SolutionAn object is moving towards a stationary plane mirror with a speed of 2 m/s. Velocity of the image w.r.t. the object is
View SolutionAn object is placed at a distance of f/2 from a convex lens. The image will be
View SolutionFigure shows a point object and a converging lens. Find the final image formed.

View SolutionAn object is placed in front of a concave lens. A virtual image of the object is formed on the same side of the lens as the object but is closer to the lens. Will rays form this image refract once again at the lens to form a second image?
View SolutionA point object O moves from the principal axis of a converging lens in a direction OP. I is the image of O, will move initially in the direction
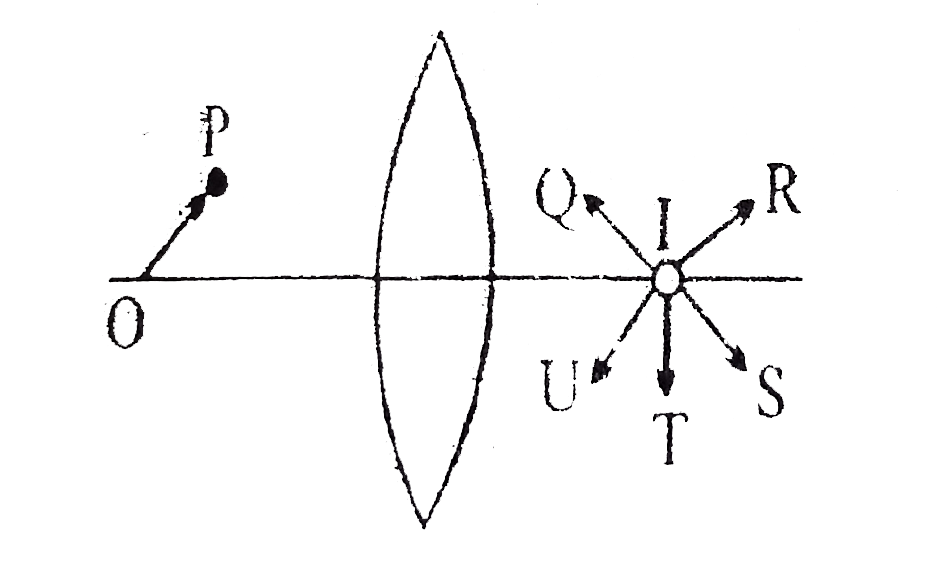
View SolutionAn object is placed in front of a converging lens at a distance greater than twice the focal length of the lens. Draw a ray diagram to show the formation of the image.
View Solution
