An optical system consists of two convergent lenses with focal length f1=20cmandf2=10cm. The distance between the lenses is d=30cm. An object is placed at a distance of 30cm from the first lens. At what distance from the second lens will the images be obtained ?
The correct Answer is:C
To solve the problem step by step, we will analyze the optical system consisting of two convergent lenses.
Step 1: Identify the parameters
We have two convergent lenses:
- Focal length of the first lens, f1=20cm
- Focal length of the second lens, f2=10cm
- Distance between the lenses, d=30cm
- Object distance from the first lens, u1=−30cm (negative because the object is on the same side as the incoming light)
Step 2: Use the lens formula for the first lens
The lens formula is given by:
1f=1v−1u
For the first lens (L1):
1f1=1v1−1u1
Substituting the values:
120=1v1−1(−30)
This simplifies to:
120=1v1+130
Step 3: Solve for v1
To solve for v1, first find a common denominator (LCM of 20 and 30 is 60):
120=360,130=260
Thus, we have:
360=1v1+260
Rearranging gives:
1v1=360−260=160
Therefore:
v1=60cm
Step 4: Determine the object distance for the second lens
The image formed by the first lens (L1) acts as the object for the second lens (L2). The distance from the first lens to the second lens is d=30cm. Therefore, the object distance for the second lens is:
u2=d−v1=30−60=−30cm
(Note: It is negative because it's on the same side as the incoming light for the second lens.)
Step 5: Use the lens formula for the second lens
Now we apply the lens formula for the second lens (L2):
1f2=1v2−1u2
Substituting the values:
110=1v2−1(−30)
This simplifies to:
110=1v2+130
Step 6: Solve for v2
Finding a common denominator (LCM of 10 and 30 is 30):
110=330,130=130
Thus, we have:
330=1v2+130
Rearranging gives:
1v2=330−130=230
Therefore:
v2=15cm
Conclusion
The final image is formed at a distance of 15cm from the second lens.
We have two convergent lenses:
- Focal length of the first lens, f1=20cm
- Focal length of the second lens, f2=10cm
- Distance between the lenses, d=30cm
- Object distance from the first lens, u1=−30cm (negative because the object is on the same side as the incoming light)
The lens formula is given by:
1f=1v−1u
For the first lens (L1):
1f1=1v1−1u1
Substituting the values:
120=1v1−1(−30)
This simplifies to:
120=1v1+130
To solve for v1, first find a common denominator (LCM of 20 and 30 is 60):
120=360,130=260
Thus, we have:
360=1v1+260
Rearranging gives:
1v1=360−260=160
Therefore:
v1=60cm
The image formed by the first lens (L1) acts as the object for the second lens (L2). The distance from the first lens to the second lens is d=30cm. Therefore, the object distance for the second lens is:
u2=d−v1=30−60=−30cm
(Note: It is negative because it's on the same side as the incoming light for the second lens.)
Now we apply the lens formula for the second lens (L2):
1f2=1v2−1u2
Substituting the values:
110=1v2−1(−30)
This simplifies to:
110=1v2+130
Finding a common denominator (LCM of 10 and 30 is 30):
110=330,130=130
Thus, we have:
330=1v2+130
Rearranging gives:
1v2=330−130=230
Therefore:
v2=15cm
The final image is formed at a distance of 15cm from the second lens.
Topper's Solved these Questions
- REFRACTION OF LIGHTBook:DC PANDEY ENGLISHChapter:REFRACTION OF LIGHTExercise:Subjective Questions
Explore 8 Videos
- REFRACTION OF LIGHTBook:DC PANDEY ENGLISHChapter:REFRACTION OF LIGHTExercise:Level 2 Single Correct
Explore 41 Videos
- REFRACTION OF LIGHTBook:DC PANDEY ENGLISHChapter:REFRACTION OF LIGHTExercise:Objective Questions
Explore 1 Video
- REFLECTION OF LIGHTBook:DC PANDEY ENGLISHChapter:REFLECTION OF LIGHTExercise:Subjective
Explore 9 Videos
- SEMICONDUCTORSBook:DC PANDEY ENGLISHChapter:SEMICONDUCTORSExercise:Subjective
Explore 12 Videos
Similar Questions
A biconvex lens of focal length 15cm is in front of a plane mirror. The distance between the lens and the mirror is 10cm. A small object is kept at distance of 30cm from the lens. The final image is
View SolutionAn object is placed at a distance of 12 cm from a convex lens of focal length 8 cm. Find :
the position of the image
View Solution
Knowledge Check
An object is place 20 cm from a diverging lens. If the distance between the lens and the image is 8 cm, what is the magnification?
A115B25C12D2
An optical system consists of a thin convex lens of focal length 30cm and a plane mirror placed 15cm behind the lens. An object is placed 15cm in front of the lens. The distance of the final image from the object is
View SolutionAn object is placed at a distance of 12 cm from a convex lens of focal length 8 cm. Find :
nature of the image
View SolutionA convex lens of focal length 10 cm is painted black at the middle portion as shown in figure. An object placed at a distance of 20 cm from the lens. Then
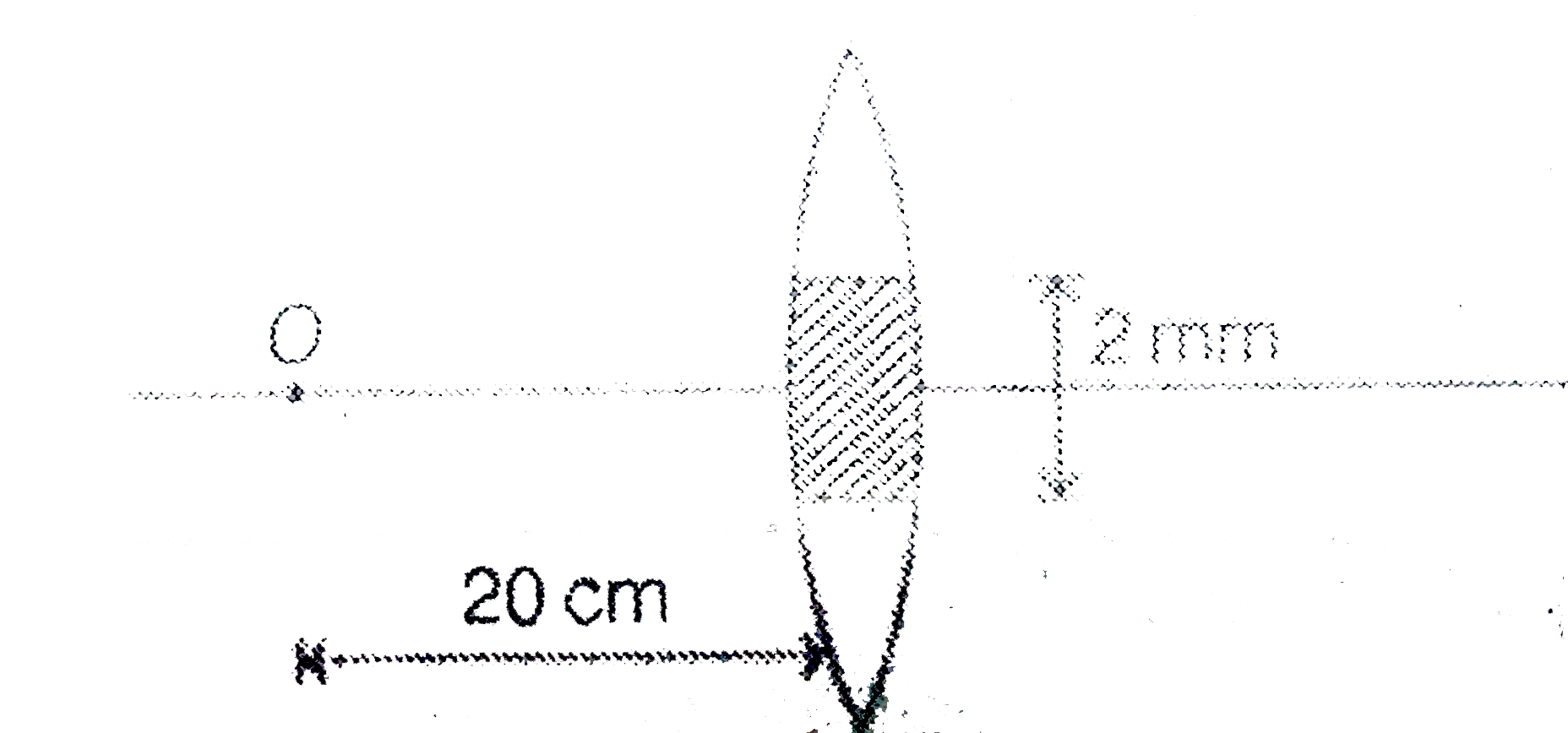
View SolutionAn object is placed at a distance of 20 cm from a concave mirror of focal lenght 10 cm. What is the image distance?
View SolutionA microscope consisting of two convex lenses of focal lengths 2 cm and 5 cm placed 20 cm apart. Where must the object be placed so that the final image (virtual) is at a distance of 25 cm from eye ?
View SolutionFind distanace of image from a convex lens of focal length
20cm if object is placed at a distance of 30cm from the lens. Also find its
magnification.
View SolutionA parallel beam of light is incident on the system of two convex lenses of focal length f1=20cm and f2=10cm . What should be the distance between the two lenses so that rays after refraction from both the lenses pass undeviated?

View Solution

