A glass sphere has radius of 5.0cm and a refractive index of 1.6. A paperweight is constructed by slicing through the sphere on a plate that is 2.0cm from the centre of the sphere and perpendicular to radius of the sphere that passes through the centre of the circle formed by the intersection of the plane and the sphere. The paperweight is placed on a table and viewed from directly above an observer who is 8.0cm from the table top, as shown in figure. When viewed through the paperweight, how far away does the table top appear to the observer?
The correct Answer is:B, C, D
To solve the problem step by step, we will use the lens maker's formula and the concepts of refraction. Here’s how we can find out how far away the table top appears to the observer:
Step 1: Identify the parameters
- Radius of the glass sphere (R) = 5.0 cm
- Refractive index of glass (μ1) = 1.6
- Refractive index of air (μ2) = 1.0
- Distance from the center of the sphere to the plane (u) = -3.0 cm (since it is measured from the center of the sphere to the plane)
- Observer's height above the table = 8.0 cm
Step 2: Calculate the object distance (u)
The object distance (u) is the distance from the object (the table) to the surface of the paperweight. Since the paperweight is 2.0 cm from the center of the sphere, the distance from the top of the sphere to the top of the paperweight is:
u=R−distance from center to plane=5.0cm−2.0cm=3.0cm
However, since we are considering the direction of light travel as positive, we take:
u=−3.0cm
Step 3: Use the lens maker's formula
Using the formula:
μ2v−μ1u=μ2−μ1R
Substituting the values:
1.0v−1.6−3.0=1.0−1.6−5.0
This simplifies to:
1.0v+1.63.0=−0.6−5.0
Calculating the right side:
1.0v+0.53331=0.12
So:
1.0v=0.12−0.5333=−0.4133
Thus:
v=−2.42cm
Step 4: Calculate the apparent distance to the observer
The observer is 8.0 cm above the table. The distance from the top of the paperweight to the table is:
Distance from observer to table=8.0cm−3.0cm=5.0cm
Now, we add the image distance (which is negative indicating it is below the table):
Apparent distance=5.0cm+2.42cm=7.42cm
Final Answer
The table top appears to be 7.42 cm away from the observer.
---
- Radius of the glass sphere (R) = 5.0 cm
- Refractive index of glass (μ1) = 1.6
- Refractive index of air (μ2) = 1.0
- Distance from the center of the sphere to the plane (u) = -3.0 cm (since it is measured from the center of the sphere to the plane)
- Observer's height above the table = 8.0 cm
The object distance (u) is the distance from the object (the table) to the surface of the paperweight. Since the paperweight is 2.0 cm from the center of the sphere, the distance from the top of the sphere to the top of the paperweight is:
u=R−distance from center to plane=5.0cm−2.0cm=3.0cm
However, since we are considering the direction of light travel as positive, we take:
u=−3.0cm
Using the formula:
μ2v−μ1u=μ2−μ1R
Substituting the values:
1.0v−1.6−3.0=1.0−1.6−5.0
This simplifies to:
1.0v+1.63.0=−0.6−5.0
Calculating the right side:
1.0v+0.53331=0.12
So:
1.0v=0.12−0.5333=−0.4133
Thus:
v=−2.42cm
The observer is 8.0 cm above the table. The distance from the top of the paperweight to the table is:
Distance from observer to table=8.0cm−3.0cm=5.0cm
Now, we add the image distance (which is negative indicating it is below the table):
Apparent distance=5.0cm+2.42cm=7.42cm
The table top appears to be 7.42 cm away from the observer.
Topper's Solved these Questions
- REFRACTION OF LIGHTBOOK - DC PANDEY ENGLISHCHAPTER - REFRACTION OF LIGHTEXERCISE - Subjective Questions
8 Videos
- REFRACTION OF LIGHTBOOK - DC PANDEY ENGLISHCHAPTER - REFRACTION OF LIGHTEXERCISE - Level 2 Single Correct
41 Videos
- REFRACTION OF LIGHTBOOK - DC PANDEY ENGLISHCHAPTER - REFRACTION OF LIGHTEXERCISE - Objective Questions
1 Videos
- REFLECTION OF LIGHTBOOK - DC PANDEY ENGLISHCHAPTER - REFLECTION OF LIGHTEXERCISE - Subjective
9 Videos
- SEMICONDUCTORSBOOK - DC PANDEY ENGLISHCHAPTER - SEMICONDUCTORSEXERCISE - Subjective
12 Videos
Similar Questions
Find the equation of sphere which passes through (1,0,0) and has its centre on the positive direction of Y-axis and has radius 2.
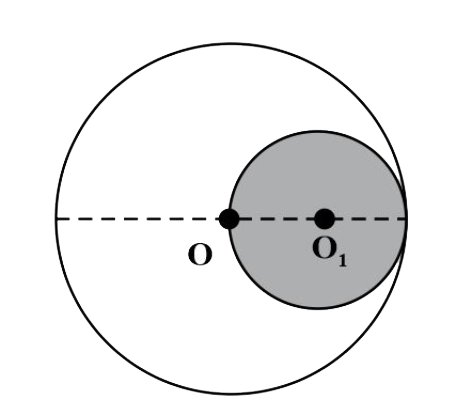
View SolutionA spherical cavity is made in a lead sphere of radius R such that its surface touches the outsides surface of lead sphere and passes through the centre. The shift in the centre of mass of the lead sphere as a result of this following, is
View SolutionAn electric dipole is placed at the centre of a sphere. Find the electric flux passing through the sphere.
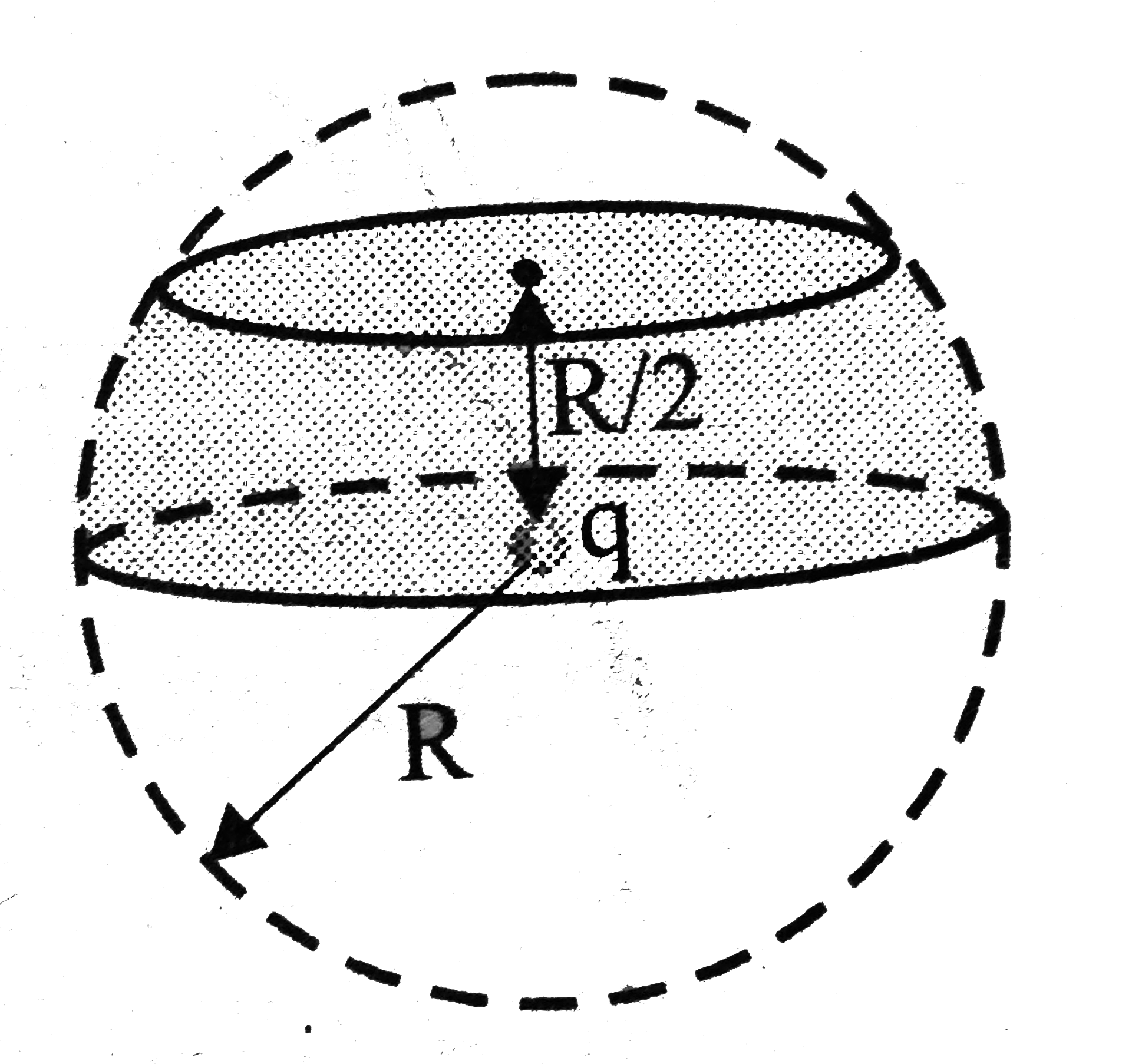
View SolutionFlux passing through the shaded surface of a sphere when a point charge q is placed at the center is (radius of the sphere is R)
View SolutionTwo spheres each of mass M and radius R/2 are connected with a massless rod of length R. Find the moment of inertia of the system about an axis passing through the centre of one of the sphere and perpendicular to the rod
View SolutionA point object is situated at a distance of 36 cm from the centre of the sphere of radius 12 cm and refractive index 1.5. Locate the position of the image due to refraction through sphere.
View SolutionAt a point 20cm from the centre of a uniformly charged dielectric sphere of radius 10cm, the electric field is 100V/m. The electric field at 3cm from the centre of the sphere will be
View SolutionThe radius of a sphere is increasing at the rate of 0.2 cm/sec. The rate at which the volume of the sphere increases when radius is 15 cm, is
View SolutionA glass sphere with 10cm radius has a 5cm radius spherical hole at its centre. A narraow beam of parallel light is directed into the sphere. Where, if anywhere, will the sphere produce an image? The index of refraction of the glass is 1.50.
View SolutionThe radius of gyration of a uniform solid sphere of radius R., about an axis passing through a point R2 away from the centre of the sphere is:
View Solution
