Two glasses with refractive indices of 1.5and1.7 are used to make two indentical double convex lenses.
Find the ratio between their focal lengths.
How will each of these lenses act on a ray parallel to its optical axis if the lenses are submerged into a transparent liquid with a refractive index of 1.6?
The correct Answer is:A, B, C, D
To solve the problem step by step, we will first find the ratio of the focal lengths of the two lenses made from glasses with refractive indices of 1.5 and 1.7. Then, we will analyze how each lens behaves when submerged in a liquid with a refractive index of 1.6.
Step 1: Finding the Focal Lengths
The formula for the focal length f of a double convex lens is given by:
1f=(n−1)(1R1−1R2)
For a double convex lens, if we assume R1=R and R2=−R (since the second radius is negative), the formula simplifies to:
1f=(n−1)(1R+1R)=(n−1)2R
Step 2: Calculate the Focal Length for Glass with Refractive Index 1.5
For the first lens with a refractive index n1=1.5:
1f1=(1.5−1)2R=0.52R=1R
Thus,
f1=R
Step 3: Calculate the Focal Length for Glass with Refractive Index 1.7
For the second lens with a refractive index n2=1.7:
1f2=(1.7−1)2R=0.72R=1.4R
Thus,
f2=R1.4
Step 4: Find the Ratio of the Focal Lengths
Now, we can find the ratio of the focal lengths f1f2:
f1f2=RR1.4=1.4
So, the ratio of the focal lengths is:
f1f2=75
Step 5: Behavior of Lenses in a Liquid with Refractive Index 1.6
Now, we need to analyze how each lens behaves when submerged in a liquid with a refractive index nl=1.6.
For Lens with n1=1.5:
Using the modified formula for the focal length in a medium:
1f1=n1nl−1⋅2R
Substituting the values:
1f1=1.51.6−1⋅2R=1.5−1.61.6⋅2R=−0.11.6⋅2R
This results in a negative focal length, indicating that the lens behaves like a diverging lens.
For Lens with n2=1.7:
Using the same modified formula:
1f2=n2nl−1⋅2R
Substituting the values:
1f2=1.71.6−1⋅2R=1.7−1.61.6⋅2R=0.11.6⋅2R
This results in a positive focal length, indicating that the lens behaves like a converging lens.
Final Summary
1. The ratio of the focal lengths of the two lenses is 75.
2. The lens made from glass with refractive index 1.5 behaves like a diverging lens when submerged in the liquid.
3. The lens made from glass with refractive index 1.7 behaves like a converging lens when submerged in the liquid.
2. The lens made from glass with refractive index 1.5 behaves like a diverging lens when submerged in the liquid.
3. The lens made from glass with refractive index 1.7 behaves like a converging lens when submerged in the liquid.
Topper's Solved these Questions
- REFRACTION OF LIGHTBook:DC PANDEY ENGLISHChapter:REFRACTION OF LIGHTExercise:Subjective Questions
Explore 8 Videos
- REFRACTION OF LIGHTBook:DC PANDEY ENGLISHChapter:REFRACTION OF LIGHTExercise:Level 2 Single Correct
Explore 41 Videos
- REFRACTION OF LIGHTBook:DC PANDEY ENGLISHChapter:REFRACTION OF LIGHTExercise:Objective Questions
Explore 1 Video
- REFLECTION OF LIGHTBook:DC PANDEY ENGLISHChapter:REFLECTION OF LIGHTExercise:Subjective
Explore 9 Videos
- SEMICONDUCTORSBook:DC PANDEY ENGLISHChapter:SEMICONDUCTORSExercise:Subjective
Explore 12 Videos
Similar Questions
Two identical thin planoconvex lenses of refractive index n are silvered, one on the plane side and other on the convex side. The ratio of their for lengths is
View SolutionA thin glass (refractive index 1.5) lens has optical power of −5D in air. Its optical power in a liquid medium with refractive index 1.6 will be
View Solution
Knowledge Check
A thin glass (refractive index 1.5) lens has optical power of −8D in air, its optical power in a liquid medium with refractive index 1.6 will be
A1DB−1DC25DD−25D
A thin glass (refractive index 1.5) lens has optical power of −5D in air. Its optical power in a liquid medium with refractive index 1.6 will be
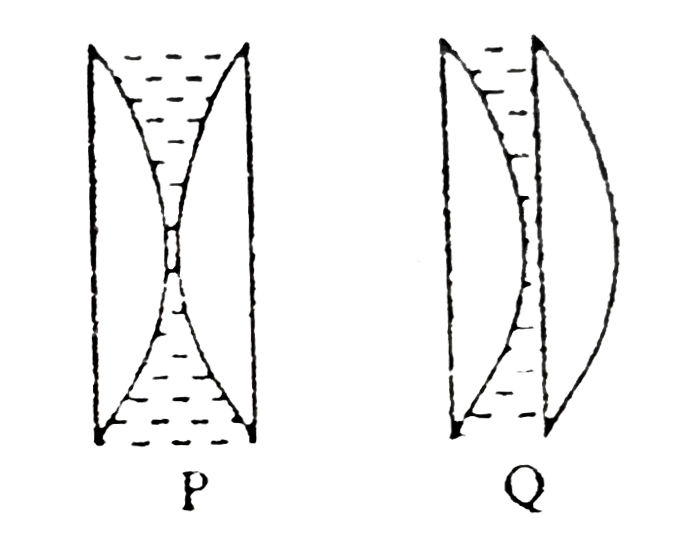
View SolutionA liquid of refractive index 1.33 is placed between two identical plano-convex lenses, with refractive index 1.50. Two possible arrangement P and Q are shown. The system is
View SolutionA double convex lens has two surfaces of equal radii R and refractive index m=1.5, we have
View SolutionA double convex thin lens made of glass of refractive index 1.6 has radii of curvature 15 cm each. The focal length of this lens when immersed in a liquid of refractive index 1.63 is :
View SolutionFocal length of a convex lens of refractive index 1.5 is 2 cm. Focal length of lens when immersed in a liquid of refractive index 1.25 will be
View SolutionA lens is made of flint glass (refractive index =1.5). When the lens is immersed in a liquid of refractive index 1.25 , the focal length:
View SolutionA double convex thin lens made of glass (refractive index μ=1.5) has both radii of curvature of magnitude 20 cm . Incident light rays parallel to the axis of the lens will converge at a distance L such that
View Solution